 |
Вывод уравнения теплопроводности (одномерный случай)
|
|
|
|
Уравнения параболического типа наиболее часто встречаются при изучении процессов теплопроводности и диффузии. К этим уравнениям приводятся также задачи о движении вязкой жидкости, например, нефти.
Рассмотрим однородный стержень длины l, теплоизолированный с боков (через поверхность не происходит теплообмена с окружающей средой) и достаточно тонкий, чтобы в любой момент времени температуру во всех точках поперечного сечения можно было считать одинаковой. Расположим ось 
так, чтобы один конец стержня совпадал с точкой 
, а другой - с точкой 
(Рис.6.8). Если тело нагрето неравномерно, то в нем происходит передача тепла из мест с более высокой температурой в места с более низкой температурой. Процесс может быть описан функцией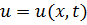 
, дающей температуру 
в каждой точке тела и в любой момент времени.
Рис.6.8.1
При выводе дифференциального уравнения теплопроводности воспользуемся следующими физическими закономерностями, связанными с распространением тепла.
1. Количество тепла 
, которое необходимо сообщить однородному телу, чтобы повысить его температуру на 
, равно
,
где 
- удельная теплоемкость,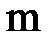 
- масса тела. Для стержня имеем
 ,
| (6.8.1) |
где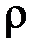 
- плотность материала стержня; 
- площадь его поперечного сечения.
2. Перенос тепла в теле подчиняется эмпирическому закону Фурье: количество тепла 
, протекающее за время 
через площадку 
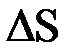в направлении нормали 
к этой площадке, равно
,
где 
- коэффициент внутренней теплопроводности (зависит от точки и не зависит от направления, если тело изотропно).
Для стержня имеем
 ,
| (6.8.2) |
где коэффициент будем считать постоянным в силу предположения о его однородности. Если стержень неоднороден, то 
.
|
|
|
3. Если внутри тела есть источники тепла, то выделение тепла можно характеризовать плотностью тепловых источников, т.е. количеством выделяемого (или поглощаемого) тепла в единицу времени в единице объема. Обозначим через 
плотность источников в точке 
рассматриваемого стержня в момент 
. Тогда в результате действия этих источников на участке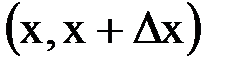 
за промежуток 
будет выделено количество тепла
 .
| (6.8.3) |
И, наконец, воспользуемся законом сохранения энергии.
Итак, приступим к выводу уравнения. Выделим элементарный участок стержня, заключенный между сечениями 
и 
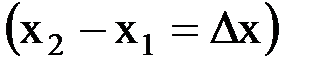, и составим уравнение теплового баланса на отрезке 
. Так как боковая поверхность стержня теплоизолирована, то элемент стержня может получать тепло только через поперечные сечения. Согласно (6.8.2) количество тепла, прошедшее через сечение 
, равно
;
через сечение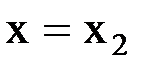 
:
.
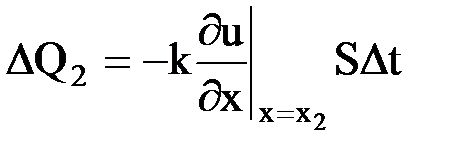Найдем приток тепла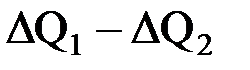 
в элемент стержня:
(К разности частных производных применена теорема Лагранжа).
Кроме того, в результате действия внутренних источников тепла на этом участке в течение времени 
выделится количество тепла согласно (6.8.3)
.
Все тепло 
за время 
пойдет на изменение температуры выделенного элемента стержня на величину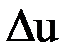 
. И поэтому сообщенное количество тепла 
, с другой стороны, может быть найдено согласно формуле (6.8.1):
.
В силу закона сохранения энергии имеем равенство
.
Сокращая на общий множитель 
, получим уравнение
.
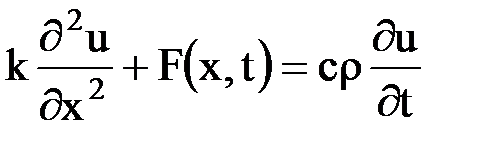Введя обозначения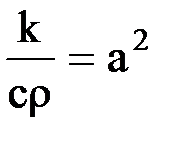 
, 
, придем к уравнению
 .
| (6.8.4) |
Это и есть искомое дифференциальное уравнение распространения тепла в однородном стержне. Уравнение (6.8.4) называют уравнением теплопроводности, в котором постоянную 
называют коэффициентом температуропроводности. Коэффициент имеет размерность м 
/с. Уравнение (6.8.4) является линейным неоднородным уравнением параболического типа.
Вывод дифференциального уравнения распространения тепла внутри тела, отнесенного к пространственной системе координат, основан на тех же физических законах. Поэтому, ограничившись выводом уравнения для простейшего случая – одномерного, лишь приведем уравнение для трехмерного пространства.
|
|
|
Процесс распределения температуры 
в изотропном теле описывается уравнением
 ,
| (6.8.5) |
которое кратко записывается так:
 ,
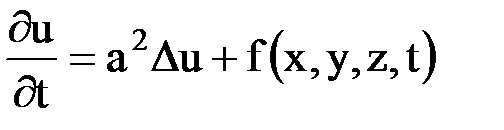| (6.8.6) |
где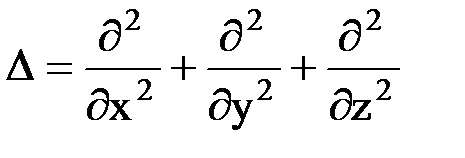 
- оператор Лапласа.
Уравнение (6.8.6) описывает также процессы диффузии, где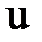 
- концентрация диффундирующего вещества, и другие.
Чтобы определить температуру внутри тела в любой момент времени, недостаточно одного уравнения (6.8.6). Необходимо, как следует из физических соображений, знать еще распределение температуры внутри тела в начальный момент времени (начальное условие) и тепловой режим на границе тела (граничное условие).
Начальное условие в отличие от уравнения гиперболического типа задается только одно, т.к. исходное уравнение содержит лишь первую производную по времени.
Граничные или краевые условия могут быть различны в зависимости от температурного режима на границе тела. Основными видами тепловых режимов являются следующие: I – на границе поддерживается определенная температура; II – на границу подается определенный тепловой поток; III – происходит теплообмен с внешней средой, температура которой известна. Им соответствуют граничные условия первого, второго, третьего рода.
Сформулируем прежде условия для одномерного уравнения теплопроводности.
Начальное условие состоит в задании функции 
в начальный момент времени 
:
 .
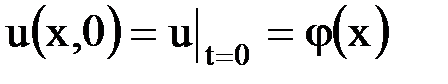| (6.8.7) |
Выведем граничные условия в случаях I – III.
1. На концах стержня (или на одном конце) задается температура
 ,  ,
| (6.8.8) |
где 
, 
- функции, заданные в некотором промежутке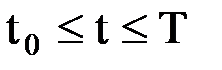 
, причем 
есть промежуток времени, в течении которого изучается процесс. В частности, 
, 
, т.е. на концах поддерживается постоянная температура 
и 
.
2. На одном из концов (или на обоих) задано значение производной искомой функции. Например, для сечения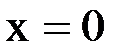 
 .
| (6.8.9) |
Дадим физическое толкование этому условию. Пусть 
- величина теплового потока, т.е. количество тепла, протекающего через торцевое сечение 
в единицу времени. Тогда уравнение теплового баланса для элемента стержня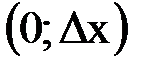 
в период времени 
, как и при выводе уравнения (6.8.4) запишется в виде
|
|
|
.
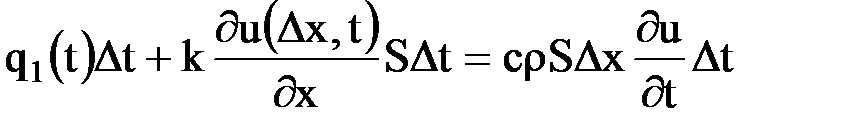Сократив на 
и перейдя к пределу при 
, получим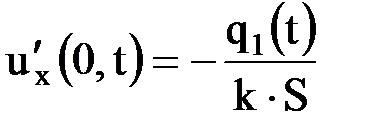 
. Таким образом, имеем условие (6.8.10), в котором 
- известная функция, выражающаяся через заданный поток тепла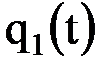 
по формуле 
.
Аналогично для сечения 
, через которое протекает количество тепла 
, найдем
.
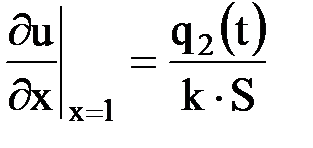Следовательно, условие 
или 
имеет место в случае, когда на соответствующем конце стержня задан тепловой поток, втекающий или вытекающий. В частности, если концевое сечение теплоизолировано, то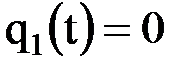 
или 
, и следовательно,
или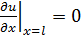 
3. На одном из концов (или на обоих) задается линейное соотношение между функцией и ее производной. Например, для сечения
 .
| (6.8.10) |
Условие (6.8.10) используется в случае процесса теплоотдачи, т.е. переноса тепла от тела к окружающей среде. Закон теплообмена сложен; но для упрощения задачи он может быть принят в виде закона Ньютона. Согласно эмпирическому закону Ньютона количество тепла, отдаваемого в единицу времени с единицы площади поверхности тела в окружающую среду, температура 
которой известна, пропорционально разности температур поверхности тела и окружающей среды:
,
где 
- коэффициент теплообмена (или внешней теплопроводности).
Можно определить тепловой поток через сечение стержня, воспользовавшись двумя выражениями в силу закона сохранения энергии. Согласно закону Ньютона тепловой поток 
, вытекающий через сечение 
, равен
.
С другой стороны, такой же тепловой поток должен подводиться изнутри путем теплопроводности. Поэтому согласно закону Фурье
.
Приравнивая правые части этих выражений, найдем
.
Отсюда получаем математическую формулировку условия в виде
,
в котором положено 
, 
.
Граничные условия, наложенные на значение производной 
, называют условиями второго рода. А условия, наложенные как на значение функции 
, так и на значение производной 
, называют условиями третьего рода.
В случае граничных условий вида (6.8.8), (6.8.9), (6.8.10) говорят соответственно о первой, второй, третьей краевых задачах для уравнения теплопроводности. Начальное условие для всех указанных краевых задач остается тем же самым и дается равенством (6.8.7).
|
|
|
Так, первая краевая задача состоит в отыскании решения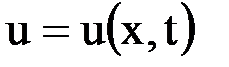 
уравнения
при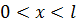 
, 
,
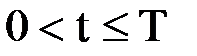удовлетворяющего условиям
, ,
, 
, 
.
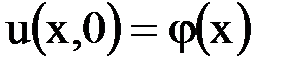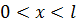Аналогично ставятся другие краевые задачи с различными комбинациями граничных условий пр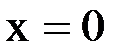и 
и .
Кроме названных задач довольно часто встречаются предельные случаи – вырождения основных краевых задач. Одним из таких случаев является задача Коши, которая состоит в отыскании решения 
в неограниченной области, удовлетворяющего только начальному условию.
Если процесс теплопроводности изучается в очень длинном стержне, таком что влияние температурного режима, заданного на границе, в центральной части стержня оказывается весьма слабым в течение небольшого промежутка времени и определяется в основном лишь начальным распределением температуры, то тогда считают, что стержень имеет бесконечную длину и ставят задачу Коши.
Задача Коши для «бесконечного» стержня (идеализация достаточно длинного стержня) математически формулируется так: найти решение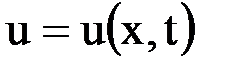 
уравнения теплопроводности в области 
, 
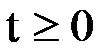, удовлетворяющее начальному условию
,
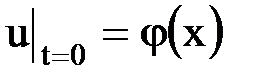
где 
- заданная функция.
Если участок стержня, температура которого нас интересует, находится вблизи одного конца и далеко от другого, то в этом случае температура практически определяется температурным режимом близкого конца и начальным условием. При этом стержень считают полубесконечным. Приведем в качестве примера формулировку первой краевой задачи для «полубесконечного» стержня: найти решение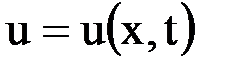 
уравнения теплопроводности в области 
, 
, удовлетворяющее условиям
, 
,
, 
,
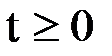где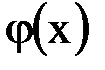 
и 
- заданные функции.
Для уравнения (6.8.6) теплопроводности в пространстве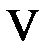 
, ограниченном поверхностью 
, начальное условие записывают в виде
,
а на границе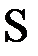 
области 
функция 
должна удовлетворять одному из условий:
1) 
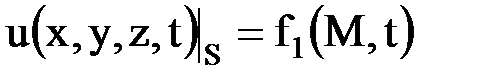(граничное условие 1-го рода);
2) 
(граничное условие 2-го рода);
где 
- внешняя нормаль к поверхности 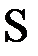; в частности, если поверхность 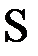теплоизолирована, то 
;
3) 
(граничное условие 3-го рода).
Здесь 
- текущая точка поверхности .
|
|
|
