Вывод дифференциального уравнения колебаний мембраны.

Мембраной называется плоская тонкая пластинка, несопротивляющаяся изгибу и сдвигу. Мембрана способна значительно прогибаться под действием поперечной нагрузки и поэтому применяется в качестве чувствительного элемента в приборах для измерения давления, в акустических приборах, упругих муфтах и т.п.

Рассмотрим мембрану (Рис.6.6.1), натянутую по контуру силой, величина которой на единицу длины равна T. Плотность единицы площади мембраны обозначим через 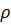. Примем, что плоскость xOy совпадает с плоскостью мембраны при ее недеформированном состоянии. Мембрана нагружена по поверхности внешней нагрузкой с интенсивностью . Предполагается что деформация мембраны мала и происходит в направлении перпендикулярном плоскости xOy.  В связи с этим так же предполагается, что натяжение мембраны и после деформации остается постоянным; увеличением площади мембраны в процессе колебаний пренебрегают. Отклонение точки мембраны от плоскости xOy обозначим через .

Рис. 6. 6.1

Для составления дифференциального уравнения колебаний мембраны из нее выделяется элемент с контуром L (Рис.6.6.2). Положительным направлением обхода этого контура принимается направление, противоположное направлению вращения часовой стрелки. На длину 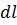 данного контура действует сила натяжения , по модулю равная .

Рис. 6. 6. 2

Равнодействующая внешней нагрузки, действующей на выделенный элемент, будет равна , а сила инерции - , где  - проекция выделенного элемента мембраны с контуром L на плоскость xOy. Проекция равнодействующей сил натяжения, действующих по контуру L, на ост Ou обозначим через 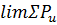, тогда согласно принципу Даламбера имеем:

 

                                  (6.6.1)

Вектор, по величине равный dl  и касательный к контуру L в точке 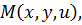 обозначим через  Единичный вектор нормали к поверхности мембраны в этой же точке обозначим через . Сила  направлена перпендикулярно плоскости, образованной векторами 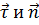, то есть она совпадает с направлением вектора  и равна векторному произведению .

Для фиксированного значения t и для случая выпуклой поверхности  направляющие косинусы углов между нормалью  и осями Ox, Oy и Ou можно определить из выражений:

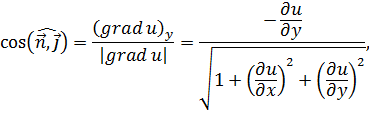
Для малых перемещений мембраны значением  по сравнению с единицей можно пренебречь, и тогда

.

Следовательно . Тогда  определяется из векторного произведения

По модулю .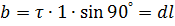

Сила  направлена по вектору

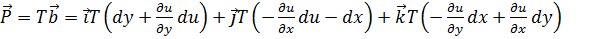(6.6.2)

Отсюда для проекции силы  на ось Ou получим

Сумма проекций всех сил натяжений, действующих по контуру направлений Ou

Подынтегральное выражение зависит только от x и y, по этому криволинейный интеграл по контуру L можно заменить криволинейным интегралом по контуру L ´.

Согласно формуле Грина

Приняв  получим

Согласно теореме о среднем можно принять

Подставляя это значение  в (6.6.1), получим

Отсюда

                                   (6.6.3)

где

Уравнение (6.6.3) есть дифференциальное уравнение вынужденных колебаний мембраны. При  получим дифференциальное уравнение свободных колебаний мембраны в виде:

(6.6.4)

Если мембрана прямоугольная и жестко закреплена по краям, то граничные условия будут:

на краях мембраны, параллельных оси Oy

(6. 6.5)

на краях мембраны, параллельных оси Ox

(6. 6.6)

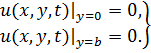
Если мембрана круглая, нагружена осесимметрично и края ее жестко закреплены, тогда перемещения сечений при 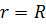 будут равны нулю, т.е.

(6. 6.7)

    Кроме того, условие

(6. 6.8)

Позволяет определить ограниченное решение. В качестве начальных условий принимаются

(6. 6.9)

 

12345

Поделиться:

Воспользуйтесь поиском по сайту: