 |
Программа физико-математической школы «Что такое математика?» при «ШЮМ»
|
|
|
|
Программа физико-математической школы «Что такое математика? » при «ШЮМ»
Программа распределяется по трем возрастным ступеням. Цели и задачи во всех трех ступенях одинаковы и формулируются следующим образом:
- совершенствование знаний, умений и навыков по стандартным школьным курсам алгебры и геометрии, создание прочной базы знаний для более эффективного изучения дальнейшего углубленного курса;
- углубленное изучение математических теорий, не входящих в школьную программу, либо неполно представленных в этой программе;
- приложение приобретенных знаний и навыков к решению задач физики, астрономии, экономики (в основном это касается учащихся 10-11 классов);
- подготовка к математическим олимпиадам;
- формирование целенаправленного эвристического (поискового), строго доказательного мышления
I ступень обучения ( 7-8 классы)
Алгебра
Формулы сокращенного умножения и тождественные преобразования алгебраических выражений. Бином Ньютона. Треугольник Паскаля.
Линейные уравнения. Решение систем из двух линейных уравнений с двумя неизвестными. Решение текстовых задач, приводящих к линейным уравнениям. Об аксиомах числового поля.
Квадратный корень. Алгоритм извлечения квадратного корня. Свойства корней, преобразования иррациональных выражений. Рациональные и иррациональные числа. Числовой континуум.
Квадратные уравнения. Теорема Виета. Простейшие задачи с параметром. Задачи на составление и решение квадратных уравнений. О графическом решении квадратных уравнений.
Свойства степеней. Степень с отрицательным показателем. Преобразования степенных выражений.
Числовые неравенства и их свойства. Доказательство числовых неравенств. Решение линейных неравенств с одной переменной. Линейные неравенства с двумя переменными. Области на координатной плоскости. Простейшие задачи линейного программирования.
|
|
|
Теория чисел
Целые и натуральные числа. Делимость целых чисел. Простые и составные числа. Решето Эратосфена. Основная теорема арифметики. Некоторые проблемы, связанные с простыми числами (в ознакомительном ключе). НОД и НОК. Деление с остатком. Арифметика остатков. Признаки делимости. Алгоритм Евклида, соотношение Безу. Взаимно простые числа. Простейшие задачи на делимость. Принцип Дирихле.
Уравнения вида 
в целых числах. Непрерывные дроби. Подходящие дроби и их свойства. Приближения чисел.
Позиционная десятичная система исчисления. Системы исчисления с другим основанием. О непозиционных системах исчисления древности.
Геометрия
«Начала» Евклида. Об аксиомах планиметрии. Признаки равенства треугольников, простейшие задачи на доказательство. Неравенство треугольника. Отражение света. Принцип Герона и принцип Ферма. О прямоугольных треугольниках.
Параллельные прямые и свойства, связанные с ними. Сумма углов треугольника. Попытки доказательства V постулата Евклида. О геометрии Лобачевского. Геометрия на сфере.
Четырехугольники. Параллелограмм и трапеция. Прямоугольник, ромб, квадрат.
Площади фигур. Теорема Пифагора. Вычисление высоты в треугольнике и трапеции.
Теорема Фалеса. Подобные треугольники. Подобные фигуры. Площади подобных фигур. Свойство биссектрисы внутреннего угла треугольника. Средняя линия в треугольнике и в трапеции. Теорема о пересечении медиан в треугольнике. Второе доказательство теоремы Пифагора. Средние геометрические величины. Соотношения отрезков и углов в прямоугольном треугольнике. Решение прямоугольных треугольников.
Четыре замечательные точки в треугольнике. Вписанная и описанная окружности для треугольника.
|
|
|
Угловое измерение дуг в окружности. Свойство вписанных углов. Вписанные и описанные четырехугольники. Понятие о геометрическом месте точек. Условие того, что четыре точки лежат на одной окружности. Свойство пересекающихся хорд. Свойство секущих и касательных.
Геометрические построения с помощью циркуля и линейки. Геометрическая алгебра. О трех классических задачах на построение.
II ступень обучения ( 9 класс)
Алгебра
Корень 
степени. Понятие степени с рациональным показателем; преобразование выражений.
Функции, их свойства и графики (линейная функция, функция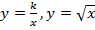 
, квадратичная функция). Построение графика квадратного трехчлена. Понятие о преобразованиях графиков. Дробно-линейная функция, кубическая функция. Графики, содержащие модуль.
Решение квадратных неравенств. Решение неравенств методом интервалов. О расположении корней квадратного трехчлена, задачи с параметром.
Задачи на максимум и минимум (элементарные методы).
Решение уравнений высоких степеней. Способ группировки, разложение на множители. Биквадратные уравнения. Другие случаи сведения к квадратному уравнению. Возвратные уравнения.
Теория алгебраического уравнения. Деление многочленов уголком. Теорема Безу. Схема Горнера. Разложение многочлена на множители. Формулы Виета. Понятие о кратных корнях.
Комплексные числа и действия над ними. Геометрическая интерпретация комплексных чисел. Тригонометрическая форма. Формула Муавра и ее приложения. Извлечение корня из комплексного числа. Решение квадратных уравнений с отрицательным дискриминантом. Основная теорема алгебры (понятие о ней). Теорема Абеля-Руффини (понятие о ней).
Формула Кардано для решения кубических уравнений. Решение кубических уравнений при помощи кубических тождеств. Метод Феррари для уравнения четвертой степени.
Последовательности. Арифметическая и геометрическая прогрессии. Метод математической индукции. Некоторые суммы. О фигурных числах. Рекуррентное задание последовательностей. Возвратные последовательности. Последовательность Фибоначчи.
Понятие о пределе последовательности. Бесконечно убывающая геометрическая прогрессия. Один старый способ приближенного извлечения корней. Длина окружности и площадь круга. Число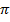 
. Сравнение роста арифметической и геометрической прогрессии. Быстро растущие последовательност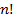и 
и 
.
|
|
|
Системы уравнений второго порядка, методы решения. Геометрическая интерпретация. Симметрические многочлены, их применение для решения систем, а также для вычисления степенных сумм. Формула Варинга. Некоторые алгебраические преобразования.
Комбинаторика и теория вероятностей Перестановки, размещения и сочетания. Решение простейших комбинаторных задач.
Случайные события. Классическое определение вероятности. Теоремы о сложении и умножении вероятностей. Формула полной вероятности. Формула Байеса. Последовательность независимых испытаний (схема Бернулли). Геометрическая вероятность. О статистическом определении вероятности. Закон больших чисел.
Случайные величины и их основные характеристики. Простейший анализ статистических данных.
|
|
|
