 |
Математическая физика. Геометрия. Топология. Теория чисел и теория групп
|
|
|
|
Математическая физика
Кривизна и соприкасающаяся окружность. Кинематика, вычисление основных кинематических величин. Понятие о дифференциальных уравнениях. Начальные примеры: 1) радиоактивный распад; 2) охлаждение тела; 3) второй закон Ньютона; 4) движение тела в среде с сопротивлением; 5) движение тела в гравитационном поле; 5) колебания: 6) реактивное движение, формула Циолковского; 7) дифференциальное уравнение вытекания воды.
Математическое описание цепных ядерных реакций. Задача о колеблющейся струне. Равновесие атмосферы, барометрическая формула. Уравнение Ван-дер-Ваальса. Скорость химической реакции. Поглощение и излучение света. Лазеры. Излучение черного тела, формула Планка. Электромагнитные колебания, переменный ток. Гидростатическое равновесие и эволюция звезд.
Геометрия
Аксиомы стереометрии. Векторно-координатное построение стереометрии. Сечения многогранников. Объемы и площади поверхности пространственных тел. Тела вращения. Некоторые теоремы о соотношении углов в тех или иных геометрических конструкциях. Формулы перехода. Трехгранные углы. Теорема Менелая для тетраэдра. Комбинации геометрических тел. Правильные многогранники. Формула Эйлера для многогранников.
Применение комплексных чисел к решению задач стереометрии.
Планиметрия (повторение). Еще раз о реализации единого алгебраического подхода к решению геометрических задач. Введение вспомогательного отрезка. Введение вспомогательного угла. Введение двух и более вспомогательных элементов. Еще раз о геометрических задачах на построение. Тригонометрические тождества при решении геометрических задач. Геометрические задачи на отыскание экстремумов. Геометрические неравенства.
|
|
|
Группы (повторение). Группы преобразования плоскости. Движения пространства. Группы самосовмещений пространственных фигур. Еще раз о правильных многогранниках. Кристаллографические группы (теория Федорова). Преобразование подобия в стереометрии.
Инверсия. Круговое свойство инверсии. Применение к проблеме Аполлония. Геометрические построения одним только циркулем. Механические приспособления для черчения. Механические кривые.
Проективные преобразования. Группа проективных преобразований. Конфигурация Дезарга. Двойное отношение точек. Полный четырехсторонник. Идеальные элементы (бесконечно удаленные точки и прямые). Проективная плоскость. Однородные координаты. Принцип двойственности. Теоремы Паскаля и Брианшона. Задачи на построение с помощью одной линейки. Снова о конических сечениях. Линейчатые кривые и поверхности.
О применении геометрических преобразований при решении задач.
Геометрия Лобачевского (повторение). Модель Клейна геометрии Лобачевского. Геометрия Римана (геометрия на сфере). Геодезические. Что такое риманова геометрия? Геометрия физического пространства. Понятие о многомерном пространстве. Евклидовы и псевдоевклидовы пространства. Пространство СТО и пространство ОТО.
Топология
Основные топологические понятия (замкнутые, открытые множества и т. д. ). Топологические преобразования (гомеоморфизмы). Связность: односвязные и многосвязные многообразия. Теорема Жордана. Проблема четырех красок. Теорема Брауэра. Узлы. Задача о кенигсбергских мостах. Уникурсуальные фигуры.
Что такое размерность? Геометрический, или комбинаторный подход к построению многомерия. Комбинаторная геометрия.
Топологическая классификация поверхностей, род поверхности. Эйлерова характеристика поверхности. Односторонние поверхности. Лист Мебиуса. Бутылка Клейна.
|
|
|
О доказательстве основной теоремы алгебры.
Теория чисел и теория групп
Еще раз о непрерывных и подходящих дробях. Уравнение Пелля. Уравнения с двумя неизвестными степени выше второй. Об алгебраических и трансцендентных числах. Теорема Лиувилля. Конструирование трансцендентных чисел.
Сравнения по модулю, вычеты (повторение). Группы, кольца и поля. Подгруппы; разложение группы по подгруппе, нормальные делители. Интерпретация теоретико-числовых теорем с групповой точки зрения. Изоморфизмы и гомоморфизмы групп. О теории Галуа. О невозможности некоторых геометрических построений циркулем и линейкой.
Большая теорема Ферма. Доказательства для случаев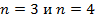 
. Теория идеальных чисел Куммера. О доказательстве теоремы в 1995 году. О нерешенных проблемах теории чисел (проблема Гольдбаха, проблема простых чисел –близнецов, проблема Коллатца и др. ).
О распределении простых чисел на числовой прямой.
|
|
|
