Доказательство с нулевым разглашением

Доказательство с нулевым разглашением

 

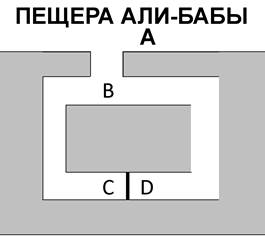
Цель: Доказывающий (Д) должен убедить проверяющего (П) в наличии у него ключа от двери C-D

1) Начало: Д - в точке В, П - в точке А

2) Д переходит случайным образом в С или D.

3) П просит Д выйти из правого (левого) коридора.

4) Д выполняет просьбу П, при необходимости воспользовавшись имеющимся ключом.

При отсутствии ключа вероятность угадывания 1А

5) Если Д правильно выполнил запрос, то итерация считается успешной, если не смог правильно выполнить - то доказательство отвергается.

6) Итерация 1)-5) повторяется n, пока не будет достигнута требуемая достоверность 1-(1/2)An. При достижении заданного уровня достоверности доказательство принимается.

Формальное определение в терминах машин Тьюринга (МТ)

Интерактивным доказательством для языка L называется пара интерактивных МТ (P(x), V(x)), где P - моделирует доказывающего, V - моделирует проверяющего, х - входное слово допустимого МТ языка L, [P(x), V(x)] - слово на выходе

Полнота

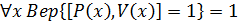
Если оба участника следуют протоколу, то доказательство будет принято

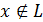Корректность  и полинома p, при  достаточно большой длины

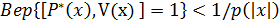
Если противник будет пытаться доказывать ложное утверждение, как угодно отклоняясь от протокола, то вероятность успеха для него пренебрежимо мала.

Нулевое разглашение

Для любой полиномиальной вероятностной МТ V*, существует вероятностная МТ M_V* работающая в среднем за полиномиальное время, т. ч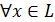

MV* (x) = [ P(x), V*(x)]

Защищает доказывающего am нечестного проверяющего:

Как бы ни отклонялся проверяющий от действий, предписанных протоколом (использует V * вместо V), он сможет при этом получить только такую информацию, которую и сам может самостоятельно вычислить в среднем за полиномиальное время.

Гамильтонов цикл в графе

Гамильтоновым циклом в графе называется непрерывный путь, проходящий через все вершины графа ровно ю одному разу.

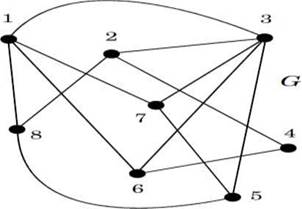
Граф с гамильтоновым циклом (8, 2, 4, 6, 3, 5, 7, 1)

Путь, проходящий последовательно через вершины 8, 2, 4, б, 3, 5, 7, 1, представляет собой гамильтонов цикл. Действительно, в этом пути содержатся все вершины графа, и каждая вершина посещается только один раз.

Ясно, что если в графе G с n вершинами гамильтонов цикл существует, то при некоторой нумерации вершин он пройдет точно через вершины с последовательными номерами 1, 2, 3,..., n. Поэтому путем перебора всех возможных нумераций вершин мы обязательно найдем гамильтонов цикл. Но количество возможных нумераций равно n!, и поэтому уже при умеренно больших n, например, при n = 100, такой подход становится практически нереализуемым. Доказано, что задача нахождения гамильтонова цикла в графе является NP-полной. Мы уже говорили кратко о понятии NP-полноты. Неформально, NP-полнота рассматриваемой задачи означает, что для ее решения не существуют (точнее, неизвестны) алгоритмы существенно более быстрые, чем указанный метод перебора.

Нашей задачей будет построение криптографического протокола, с помощью которого Алиса будет доказывать Бобу, что она знает гамильтонов цикл в некотором графе G так, чтобы Боб не получил никаких знаний о самом этом цикле. Иными словами, Алиса будет предоставлять Бобу доказательство с нулевым знанием. Еще раз напомним читателю, что «нулевое знание» означает, что независимо от числа реализаций протокола доказательства Боб будет располагать точно такими же сведениями о гамильтоновом цикле, какие он мог бы получить, просто изучая представленный ему граф G.

Итак, допустим, что Алиса знает гамильтонов цикл в графе G. Теперь она может это доказывать Бобу и всем, кто имеет граф G) с помощью описываемого ниже протокола. Алиса может использовать это доказательство, например, для идентификации своей личности. Но прежде чем мы перейдем к описанию протокола, договоримся о некоторых обозначениях.

Мы будем обозначать графы буквами G, H, F, понимая под этим одновременно соответствующие матрицы смежности. Элемент матрицы H_ij = 1, если в графе H есть ребро, соединяющее вершины i и j; H_ij = 0 в противном случае. Символом || будем обозначать конкатенацию (сцепление) двух чисел, точнее, двоичных слов, им соответствующих. Нам понадобится шифр с открытым ключом. Во-соответствующих. Нам понадобится шифр с открытым ключом. Вообще говоря, это может быть любой шифр, но для определенности будем использовать шифр RSA (разд. 2. 6). Будем считать, что Алиса сформировала систему RSA с открытыми параметрами N и d. Важно, что зашифрованные в этой системе сообщения может расшифровать только Алиса и больше никто.

Протокол доказательства состоит из следующих четырех шагов (пояснения будут даны ниже).

Шаг 1. Алиса строит граф Н, являющийся копией исходного графа G, где у всех вершин новые, случайно выбранные номера. На языке теории графов говорят, что Н изоморфен G. Иными словами, Н получается путем некоторой перестановки вершин в графе G (с сохранением связей между вершинами). Алиса кодирует матрицу Н, приписывая к первоначально содержащимся в ней нулям и единицам случайные числа r_ij по схеме r_ij||H_ij. Затем она шифрует элементы матрицы Н, получая зашифрованную матрицу F, F_ij — H_ij^d mod N. Матрицу F Алиса передает Бобу.

 

 

Шаг 2. Боб, получив зашифрованный граф F, задает Алисе один из двух вопросов.

1. Каков гамильтонов цикл для графа Н?

2. Действительно ли граф Н изоморфен G?

Шаг 3. Алиса отвечает на соответствующий вопрос Боба.

1. Она расшифровывает в F ребра, образующие гамильтонов цикл.

2. Она расшифровывает F полностью (фактически передает Бобу граф Н) и предъявляет перестановки, с помощью которых граф Н был получен из графа G.

Шаг 4. Получив ответ, Боб проверяет правильность расшифровки путем повторного шифрования и сравнения с F и убеждается либо в том, что показанные ребра действительно образуют гамильтонов цикл, либо в том, что предъявленные перестановки действительно переводят граф G в граф Н.

Весь протокол повторяется t раз.

Обсудим вначале кратко несколько вопросов по построению протокола.

1. Зачем Алиса строит изоморфный граф? Если бы она этого не делала, то Боб, получив ответ на свой вопрос номер один, узнал бы гамильтонов цикл в графе G.

2. Зачем Алиса кодирует матрицу H? С этим приемом мы уже встречались при шифровании цветов вершин графа. Дело в том, что невозможно зашифровать непосредственно нули и единицы (с помощью шифра RSA они вообще не шифруются). Даже если заменить их на какие-то произвольные числа а и! >, то мы получим всего два различных шифротекста, н Бобу не составит труда понять, какой из них какому числу соответствует. Т. е. структура графа не будет скрыта. Здесь мы стал киваем ся с типичной ситуацией, когда требуется использовать так называемый рандомизированный шифр. II такой шифр строится путем добавления случайных чисел в матрицу Н перед шифрованием. Закодированная матрица Н точно также задает граф (нечетность числа означает наличие ребра, четность -его отсутствие), но после шифрования Н структура графа полностью сбывается (мы используем известное свойство шифра RSA — он полностью скрывает четность числа [36]).

3. Зачем Боб задает два вопроса? Если бы он задавал только вопрос номер один, который по смыслу протокола является основным, то Алиса, не зная в действительности гамильтонова цикла в графе G, могла бы предъявить Бобу совсем другой граф с таким же количеством вершин и искусственно заложенным в него гамильтоновым циклом. Поэтому Боб иногда просит Алису доказать изоморфизм графов Н и G. Важно, что Алиса не знает заранее, какой из двух вопросов задаст Боб.

4. Почему Боб не может задать сразу двух вопросов? В этом случае он узнал бы гамильтонов цикл в G, так как ему был бы показан гамильтонов цикл в H и правило перехода от H к G.

5. Зачем Боб проверяет правильность расшифровки? Если бы он этого не делал, то Алиса на четвертом шаге могла бы предоставить ему «выгодную» для себя информацию, а не ту, которую она посылала ему на втором шаге.

Более точно основные детали протокола обосновываются в ходе доказательства двух основных утверждений.

Утверждение. Вероятность обмана при t реализациях протокола не превосходит 2^-t.

Доказательство. Вначале покажем, что вероятность обмана в одной реализации протокола равна 1/2. Заметим, что если Алиса действительно знает гамильтонов цикл в графе G, то она может правильно ответить на любой вопрос Боба. Если же она не знает гамильтонов цикл, то самое большее, что она может сделать, — это подготовиться к ответу на первый либо на второй вопрос. В ожидании первого вопроса, она создает новый граф с искусственно заложенным в него гамильтоновым циклом. Но в этом случае она не сможет доказать его изоморфизм графу G. В ожидании второго вопроса, она строит граф, изоморфный графу G. Но в этом случае она не сможет показать в нем гамильтонов цикл. Таким образом, вероятность успешности обмана равна вероятности угадывания номера вопроса. В предположении, что Боб задает оба вопроса с одинаковыми вероятностями, мы получаем, что вероятность обмана равна 1/2.

Так как Боб прекращает игру при первом же неправильном ответе, вероятность обмана при / реализациях протокола не превосходит (1/2)^t.

Утверждение. Представленный протокол реализует доказательство с нулевым знанием.

Доказательство. Чтобы доказать, что Боб не получает никаких знаний в ходе реализации протокола, достаточно показать, что все, что он получает от Алисы, он мог бы получить сам, не вступая с ней ни в какое общение.

Рассмотрим вначале второй вопрос Боба. В ответ на этот вопрос он получает граф, изоморфный графу G. Но он сам мог строить сколько угодно изоморфных графов, и то, что присылает ему Алиса, это просто один из них.

Случай с первым вопросом не столь очевиден. В ответ на первый вопрос Боб получает гамильтонов цикл в графе, изоморфном графу G. На первый взгляд может показаться, что это дает Бобу какую-то информацию. Однако это не так. Заметим, что если в G есть гамильтонов цикл, то при некоторой нумерации вершин существует.

Таким образом, Боб не получает от Алисы никакой информации, которую он не мог бы получить сам.

Пример. Возьмем в качестве основного граф G, изображенный на рис. Его матрица смежности имеет вид

 

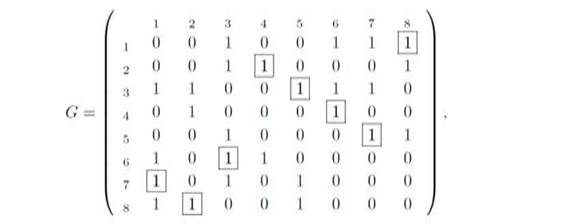
В матрице с помощью  показан гамильтонов цикл. Алиса выбирает некоторую случайную нумерацию вершин, скажем, 7, 4, 5, 3, 1. 2, 8, 6, п получает изоморфный граф

Для шифрования матрицы будем использовать систему RSA с параметрами N = 55, d = 3. Вначале закодируем матрицу Н. В рамках данного примера просто припишем слева к каждому элементу матрицы выбираемую случайно с равными вероятностями цифру из множества {1, 2, 3, 4, 5}:

Теперь мы шифруем матрицу Н, возводя каждый ее элемент в куб по модулю 55:

Боб получает матрицу t и задает один из двух вопросов. Если он просит доказать изоморфизм графов, то Алиса просто посылает ему кодированную матрицу Н и использованную нумерацию 7, 4, 5, 3, 1, 2, 8, 6. Боб проверяет соответствие матрицы Н матрице F, т. е. выполнение равенств 50³ mod 55 = 40, 20³ mod 55 = 25 и т. д. Из матрицы Н Боб получает граф Н (просто отбросив стартую десятичную цифру). Затем он переставляет вершины графа Ст в соответствии с полученной нумерацией, как это делала Алиса, и убеждается в том, что Н и О один и тот же граф.

Если Боб просит показать ему гамильтонов цикл, то Алиса посылает ему соответствующий список (закодированных) ребер графа Н: (1, 5, 21), (5, 7, 41), (7, 6, 21), ..., (3, 1, 41). Каждый элемент содержит номера вершин и код ребра. Боб проверяет соответствие указанных в списке ребер матрице F, например, 21³ mod 55 = 21 = F_{1, 5}, 41³ mod 55 = 06 = F_{5, 7} и т. д. Затем он убеждается, что указанный в списке путь проходит через все вершины графа по одному разу.

⇐ Предыдущая16171819202122232425Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: