 |
Математические основы криптографии
|
|
|
|
Математические основы криптографии
Определение (функция Эйлера). Пусть дано целое число N > 1. Значение функции Эйлера 
равно количеству чисел в ряду 1, 2, 3, …, N-1, взаимно простых с N.
Пример
Утверждение Если p - простое число, то 
Доказательство. В ряду 
все числа взаимно просты с р. так как р - простое число и по определению не делится ни на какое другое число.
Утверждение Пусть p и q – два различных простых числа 
. Тогда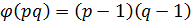 
.
Доказательство. В ряду 1, 2, …, pq-1 не взаимнопростыми с pq будут числа
Всего таких чисел будет (q-1)+(p-1). Следовательно, количество чисел, взаимнопростых с pq, будет
Теорема (Эйлер). Пусть a и b – взаимно простые числа. Тогда
Теорема Если p и q – простые числа, 
и k – произвольное целое число, то
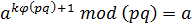
Теорема (Ферма). Пусть p – простое число и 0 < a < p. Тогда
Шифр Шамира
Этот шифр, предложенный Шамиром (Adi Shamir), был первым, позволяющим организовать обмен секретными сообщениями по открытой линии связи для лиц. которые не имеют никаких защищенных каналов и секретных ключей и. возможно, никогда не видели друг друга.
Перейдем к описанию системы. Пусть есть два абонента А и В, соединенные линией связи. A хочет передать сообщение m абоненту B так. чтобы никто не узнал его содержание. A выбирает случайное большое простое число р и открыт передает его В. Затем A выбирает два числа cA и dA, такие что
Эти числа А держит в секрете и передавать не будет. В тоже выбирает два числа cB и dB, такие что
и держит их в секрете.
В настоящее время такой шифр, как правило, используется для передачи чисел, например, секретных ключей, значения которых меньше p. Таким образом, мы будем рассматривать только случай m < p. Дадим описание протокола.
|
|
|
Шаг 1. A вычисляет число
где m – исходное сообщение, и пересылает x1 к B.
Шаг 2. B, получив x1, вычисляет число
и передает x2 к A.
Шаг 3. A вычисляет число
и передает его B.
Шаг 4. B, получив x3, вычисляет число
Утверждение (свойства протокола Шамира).
1) 
, т. е. в результате реализации протокола от А к В действительно передается исходное сообщение;
2) злоумышленник не может узнать, какое сообщение было передано.
Доказательство. Вначале заметим, что любое целое число 
может быть представлено в виде 
, где 
. Поэтому на основании теоремы Ферма
.
Справедливость первого пункта утверждения вытекает из следую щей цепочки равенств:
Доказательство второго пункта утверждения основано на предположении, что для злоумышленника, пытающегося определить m, не существует стратегии более эффективной, чем следующая. Вначале он вычисляет 
, затем находит 
и, наконец, вычисляет 
Но для осуществления этой стратегии злоумышленник должен решить задачу дискретного логарифмирования, что практически невозможно при больших р.
нента A. так как действия для B совершенно аналогичны. Число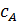 
выбираем случайно так. чтобы оно было взаимно простым с р - 1 (поиск целесообразно вести среди нечетных чисел, так как р - 1 четно). Затем вычисляем 
с помощью обобщенного алгоритма Евклида.
Шифр эль-гамаля
Пусть имеются абоненты А, В, С, ..., которые хотят передавать друг другу зашифрованные сообщения, не имея никаких защищенных каналов связи. В этом разделе мы рассмотрим шифр, предложенный Эль-Гамалем (Taher ElGamal), который решает эту задачу, используя, в отличие от шифра Шамира, только одну пересылку сообщения. Фактически здесь используется схема Диффи-Хеллмана, чтобы сформировать общий секретный ключ для двух абонентов, передающих друг другу сообщение, и затем сообщение шифруется путем умножения его на этот ключ. Для каждого следующего сообщения секретный ключ вычисляется заново. Перейдем к точному описанию метода.
|
|
|
Для всей группы абонентов выбираются некоторое большое простое число р и число д, такие что различные степени д суть различные числа по модулю р Числа р и д передаются абонентам в открытом виде (они могут использоваться всеми абонентами сети).
Затем каждый абонент группы выбирает свое секретное число ci, 1 < ci < р - 1, и вычисляет соответствующее ему открытое число di,
В результате получаем таблицу
|
|
|
