 |
Протокол аутентификации Фиата – Шамира
|
|
|
|
Протокол аутентификации Фиата – Шамира
Относится к числу протоколов «нулевого разглашения». Основан на сложности задачи извлечения корня (аналогична факторизации)
1. Предварительный этап.
1. 1. Доверенный центр T выбирает два простых числа p и q, рассылает всем доказывающим число n=pq.
1. 2. А выбирает секрет s, т. ч. (s, n)=1, 1< s< n-1 вычисляет v = s2 (mod n),
2. Итерация.
2. 1. А выбирает случайное z, т. ч. 1< z< n-1 вычисляет x = z2 (mod n), отправляет x проверяющему B
2. 2. B выбирает случайный бит с и отправляет его А
2. 3. А вычисляет y =z, если с = 0 y =zs, если с = 1 и отправляет у проверяющему B
2. 2. B принимает итерацию, если у2 = xvc (mod n).
Комментарий.
Полнота - непосредственно следует из вычисления формулы
Корректность. Например, пусть некто пытается выдать себя за А, подбирая значение х, не зная секрета: x= z2 / v.
Тогда он сможет дать правильный ответ при c=1, но не сможет ответить правильно при с=0, (надо вычислить корень из V, что является труднорешаемой задачей).
Криптография на основе эллиптических кривых
Эллиптические кривые
Эллиптические кривые - другой криптографический способ на основе открытых ключей
Эллиптические кривые могут быть более эффективными
Меньше битов требуется для той же безопасности
Но операции являются более сложными
Эллиптическая кривая E является графиком уравнения вида
y2 = x3 + ax + b
Также включает в себя «точку на бесконечности»
Как выглядят эллиптические кривые?
Эллиптические кривые как алгебраические / геометрические объекты широко изучались в течение последних 150 лет, и из этих исследований появилась богатая и глубокая теория. Системы с эллиптическими кривыми применительно к криптографии были впервые предложены в 1985 году независимо Нилом Коблицем из Вашингтонского университета и Виктором Миллером, который тогда работал в IBM, Yorktown Heights
|
|
|
Многие криптосистемы часто требуют использования алгебраических групп. Эллиптические кривые могут использоваться для формирования групп эллиптических кривых.
Эллиптические кривые сначала исследуются над действительными числами, чтобы проиллюстрировать геометрические свойства групп эллиптических кривых. После этого исследуются группы эллиптических кривых с базовыми полями Fp (где p - простое число) и F2m (двоичное представление с элементами 2m)
Эллиптическая кривая над действительными числами может быть определена как набор точек (x, y), которые удовлетворяют уравнению эллиптической кривой в виде: y2 = x3 + ax + b, где x, y, a и b – действительные числа.
Каждый выбор чисел а и b дает различную эллиптическую кривую. Например, а = -4 и b = 0, 67 дает эллиптическую кривую с уравнением
y2 = x3 - 4х + 0, 67;
Если х3 + ax + b не содержит повторяющихся факторов или, что то же самое, если 4а3 + 27b2 не равно 0, то эллиптическая кривая y2 = x3 + ax + b может быть использована как группа.
Группа эллиптических кривых над действительными числами состоит из точек на соответствующей эллиптической кривой вместе со специальной точкой O, называемой точкой на бесконечности.
Эллиптической кривой Сложение: Геометрический подход
Эллиптические группы кривой - аддитивные группы; их основная функция является дополнением. Сложение двух точек эллиптической кривой определяется геометрически.
Отрицательная точка Р = (Xp, Yp) является ее отражением в оси х: точка -P есть (Xp, -yP). Обратите внимание, что для каждой точки Р на эллиптической кривой, точка -P также находится на кривой.
Математические основы
Кривая третьего порядка E, задаваемая уравнением вида
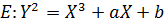
называется эллиптической кривой (на самом деле уравнение получено путем замены переменных из более общего уравнения. которое нас не будет интересовать).
|
|
|
Поскольку 
, график кривой симметричен относительно оси абцисс. Чтобы найти точки его пересечения с осью абцисс, необходимо решить кубическое уравнение
|
|
|
