Электронно-цифровая подпись. Симметричная система шифрования. Алгоритм подписи. Схема проверки подписи вида. Подписывающий

Электронно-цифровая подпись

Число, зависящее от сообщения и от некоторого секретного, известного только подписывающему субъекту ключа.

Легко проверяема, проверку подписи может осуществить каждый без получения доступа к секретному ключу.

При возникновении спорной ситуации (отказ от подписи, подделка подписи), третья сторона должна иметь возможность разрешить спор.

Таким образом, решаются три задачи: аутентификация источника сообщения, установление целостности сообщения, невозможность отказа от подписи конкретного сообщения.

ЭЦП включает два алгоритма:

Алгоритм вычисления подписи и Алгоритм проверки подписи.

Основные требования:

Исключить возможность получения подписи без знания секретного ключа. Гарантировать возможность проверки подписи без знания секретного ключа.

Надежность подписи обеспечивается сложностью трех задач:

• Подделки подписи (нахождение значения подписи лицам, не являющимся владельцем ЭЦП)

• Создания подписанного сообщения (нахождение хотя бы одного сообщения с правильным значением подписи)

• Подмены сообщения (подбор двух разных сообщений с одинаковым значением подписи)

Симметричная система шифрования

1. Схемы на основе симметричных систем шифрования.

2. Схемы на основе специально разработанных алгоритмов вычисления и проверки подписи.

3. Схемы на основе шифрования с открытыми ключами (с восстановлением текста. )

(E, D) - пара преобразований, А - автор, П- получатель, М - сообщение, S - подпись автора.

E зависит от открытого ключа, D - от секретного.

A: S=D(M)

П: E(S)= M.

Требования: M= E (D(M)) для всех M; невозможно вычислить D(M) без знания секретного ключа. Возможно: данные подписываются, потом шифруются.

Основан на вычислении логарифма в конечном поле.

p- простое число,

Z(p) - конечное поле, w - примитивный элемент в Z(p).

Выбрать случайное число 1< а < р -2 (а - секретный ключ).

Вычислить b= w^а mod p.

((p, w, b)- открытый ключ).

Алгоритм подписи

1. Выбрать случайное число 1≤ r ≤ p -2;

2. Вычислить c = w^r mod p;

3. Для x=M вычислить d = (x- a-c)r^-1 mod (p-1);

4. S=(c, d).

Алгоритм проверки. b^с c^d = w^x (mod p).

Замечания.

1. Число r должно уничтожаться сразу после вычисления подписи. Иначе секретный ключ вычисляется

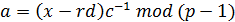
2. Число r должно быть случайным, не должно повторяться для разных подписей. На шаге 3 реально обычно берется не x=M, а x=h(M) - свертка, полученная с помощью хэш-функции.

3. На одном секретном ключе можно выработать ЭЦП для многих сообщений

Схема проверки подписи вида

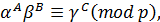
где (А, В, С) — перестановка элементов (±x, ±d, ±c) заложена во многих стандартных алгоритмах ЭЦП, в том числе в ГОСТ 34-10-94 и DSS.

Нужно подписать сообщение M=(m₁m₂…m_n), где m_i из {0, 1}

Подписывающий

1) выбирает

2п случайн. секретных ключей:

2п случайных чисел из {0, 1}:

2) вычисляет

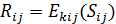, где  j из {0, 1}, i=1, 2,..., n

3) Публикует наборы

S и R=[(R₁₀, R₁₁), (R₂₀, R₂₁)> …, (R_n0, R_n1)]

Подпись для M имеет вид (k_1m1, k_2m2, ..., k_nmn)

Проверка подписи: 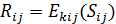, где j=m_i, i=1, 2, …, n

Недостатки:

1) Слишком большой размер ключа

Можно хранить только секретный ключ k, и на его основе формировать всю последовательность

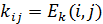
2) После проверки весь секретный ключ или его часть становится известны проверяющему, поэтому система одноразовая.

Инфраструктура открытых ключей

ИОК необходима для исключения возможности подделки открытого ключа лицами, которые хотели бы выдать себя в качестве владельца секретного ключа.

ИОК включает в себя сеть центров сертификации открытых ключей.

Цель - обеспечить подтверждение достоверности принадлежности открытого ключа заявленному владельцу.

⇐ Предыдущая14151617181920212223Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: