 |
Таблица Ключи пользователей в системе Эль-Гамаля
|
|
|
|
Таблица Ключи пользователей в системе Эль-Гамаля
| Абонент | Секретный ключ | Открытый ключ |
| А | cA | dA |
| В | cB | dB |
| С | cC | dC |
Покажем теперь, как А передает сообщение m абоненту B. Будем предполагать, как и при описании шифра Шамира, что сообщение представлено в виде числа m < p.
Шаг 1. А формирует случайное число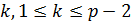 
, вычисляет числа
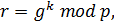
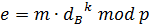
и передает пару чисел (r, е) абоненту В.
Шаг 2. получив (г, е), вычисляет
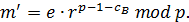
Утверждение (свойства шифра Эль-Гамаля).
1) Абонент В получал сообщение, т. е. m' = m;
2) противник, зная p, g, dB, r и e, не может вычислить m
Доказательство.
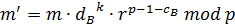
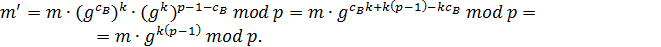
По теореме Ферма
и. таким образом, мы получаем первую часть утверждения.
Для доказательства второй части заметим, что противник не может вычислить k, так как это задача дискретного логарифмирования. Следовательно, он не может вычислить m так как m было умножено на неизвестное ему число. Противник также не может воспроизвести действия законного получателя сообщения (абонента В), так как ему не известно секретное число cB (вычисление cB — также задача дискретного логарифмирования).
Пример
Передадим сообщение m = 15 от А к В. Выберем параметры аналогично тому, как это было сделано в примере.
Возьмем р = 23, g = 5. Пусть абонент В выбрал для себя секретное число cB = 13 и вычислил
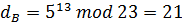
Абонент А выбирает случайно число k, например k = 7, и вычисляет:
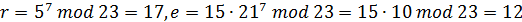
Теперь А посылает к В зашифрованное сообщение в виде пары чисел (17, 12). В вычисляет
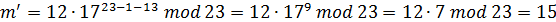
Мы видим, что В смог расшифровать переданное сообщение.
Ясно, что но аналогичной схеме могут передавать сообщения все абоненты в сети. Заметим, что любой абонент, знающий открытый ключ абонента В, может посылать ему сообщения, зашифрованные с помощью открытого ключа dB. Но только абонент J5, и никто другой, может расшифровать эти сообщения, используя известный только ему секретный ключ cB. Отметим также, что объем шифра в два раза превышает объем сообщения, но требуется только одна передача данных (при условии, что таблица с открытыми ключами заранее известна всем абонентам).
|
|
|
Криптография с открытым ключом
В основе теоретико-сложностный подход.
Односторонние функции F: X→ Y
а) существует полиномиальный алгоритм вычисления
y=F(x);
б) не существует полиномиального алгоритма инвертирования функции F, т. е. решения уравнения
F(x)=y относительно x.
Более сильное требование, чем принадлежность к NP-полным проблемам, т. к. требуется отсутствие полиномиального алгоритма почти всюду.
Функция с секретом fK: X→ Y
а) при любом к существует полиномиальный алгоритм вычисления fK;
б) при неизвестном к не существует полиномиального алгоритма инвертирования данной функции;
в) при известном к существует полиномиальный алгоритм ее инвертирования.
Дифи У., Хеллман М. Защищенность и имитостойкость. Введение в криптографию // ТИИЭР т. 67, №3, 1979
RSA
Алгоритм шифрования, в основе сложная задача факторизации больших чисел
1. Абонент выбирает пару простых чисел: p и q вычисляет и публикует n=pq
2. Функция Эйлера: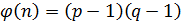 
3. Случайное e
4. Вычисляем d: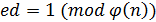 
5. Открытый ключ; (n, e)
6. Секретный ключ: (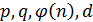 
)
Шифрование: 
Расшифрование: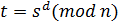 
Задача. Зашифровать аббревиатуру RSA при p=17, q=31.
Решение
1) Вычисляем модуль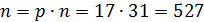 
2) Функция Эйлера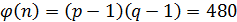 
3) Случайное е, т. ч.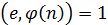 
, например е = 7.
4) Вычисляем d, т. ч. e d=1(mod 480), d=343, т. к.
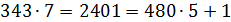
5) Переведем слово «RSA» в числовой вид:
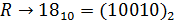
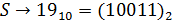
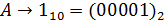
Общая последовательность (с учетом диапазона [0, 526]):
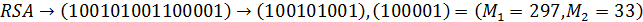
6) Шифруем последовательно M1 и M2
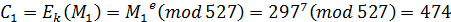
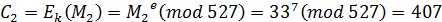
Получаем шифрограмму: С= (474, 407)
7) Расшифрование
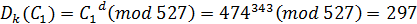
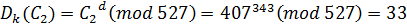
Для упрощения вычислений можно использовать соотношение:
343=256+64+16+4+2+1
|
|
|
Домашнее задание: написать программу на языке, реализующую RSA, проверить Пример для теста - зашифровать и расшифровать последовательность, включающую свои имя и фамилию (без пробела) + 3 собственных примера.
|
|
|
