 |
1.5.1 Нумерация объектов на диаграммах IDEF0
|
|
|
|
1. 5. 1 Нумерация объектов на диаграммах IDEF0
Каждому объекту (блоку) на диаграмме присваивается номер, помещаемый в нижнем правом внутреннем углу блока. Эта система нумерации необходима для однозначной идентификации блоков в пределах диаграммы и для генерации узловых номеров. Эти номера используются также для ссылок на блоки в тексте и глоссарии.
На контекстной диаграмме А-0 единственному блоку присваивается номер 0 (нуль). На всех других диаграммах блоки нумеруются цифрами от 1 до 6, начиная с верхнего левого блока (при их диагональном размещении) и кончая нижним правым блоком. Если некоторые блоки на диаграмме размещены не по диагонали, то сначала нумеруются «диагональные» блоки (также начиная с левого верхнего блока), а затем – «недиагональные» блоки, начиная с нижнего правого против часовой стрелки.
1. 5. 2 Узловые номера
Узловой номер базируется на положении блока в иерархии модели. Обычно узловой номер формируется добавлением номера блока к номеру диаграммы, на которой он появляется [1]:
| А | * | * | * | * | * | ||||||||
| и т. д. | |||||||||||||
| номер блока на диаграмме А42 | |||||||||||||
| номер блока на диаграмме А4 | |||||||||||||
| номер блока на диаграмме А0 | |||||||||||||
| имя блока А0 | |||||||||||||
Буквенный индекс А вводится условно. Когда родительский блок подробно описывается дочерней диаграммой, узловые номера родительского блока и дочерней диаграммы совпадают.
|
|
|
Контекстные диаграммы и дочерняя диаграмма верхнего уровня – исключения в вышеуказанной схеме узловой нумерации. Поскольку каждая модель IDEF0 имеет контекстную диаграмму верхнего уровня – диаграмму А-0, то эта диаграмма содержит единственный «высший блок», который является уникальным родителем всей модели и несет уникальный номер 0 (нуль) и узловой номер А0. Каждая модель IDEF0 должна также иметь по крайней мере одну дочернюю диаграмму, содержащую декомпозицию блока А0 на 3... 6 дочерних блоков. Этим блокам присваиваются уникальные узловые номера А1, А2, A3, ... А6. Таким образом, последовательность [А0, Al,..., A2,..., A3,... ] начинает нумерацию узлов для любой модели.
Например, модель может иметь следующие узловые номера:
| А-1 | Дополнительная контекстная диаграмма | |
| А-0 | Обязательная контекстная диаграмма верхнего уровня (содержащая высший блок АО) | |
| А0 | Верхняя дочерняя диаграмма | |
| А1, А2, ..., А6 | Дочерние диаграммы | |
| А11, А12, ...., А16, ...., А61, ..., А66 | Дочерние диаграммы | |
| А111, А112, ..., А161, ...., А611, ..., А666 | Дочерние диаграммы | |
| … | Дочерние диаграммы нижнего уровня | |
Узловой номер используется также для обозначения того, что блок подвергнут декомпозиции. В этом случае узловой номер, совпадающий с номером дочерней диаграммы, помещается под правым нижним углом блока на родительской диаграмме (рисунок 4).
1. 5. 3 Дерево узлов (функций)
Разработанная модель IDEF0 со всеми уровнями структурной декомпозицией может быть представлена на единственной диаграмме в виде дерева узлов (функций), дополняющего перечень узлов. Для изображения этого дерева нет стандартного формата. Единственное требование состоит в том, что вся иерархия узлов модели должна быть представлена наглядно и понятно. Пример дерева функций показан на рисунке 15 [6].
|
|
|

Рисунок 15 – Диаграмма дерева функций
1. 6 Построение диаграмм IDEF0
1. 6. 1 Правила построения диаграмм IDEF0
При построении диаграммы в нотации IDEF0 необходимо придерживаться следующих правил [1] [2]:
1) в составе модели должна присутствовать контекстная диаграмма А-0, которая содержит только один блок. Номер единственного блока на контекстной диаграмме А-0 должен быть 0;
2) блоки на диаграмме должны располагаться по диагонали – от левого верхнего угла диаграммы до правого нижнего в порядке присвоенных номеров. Блоки на диаграмме, расположенные вверху слева «доминируют» над блоками, расположенными внизу справа. Расположение блоков на листе диаграммы отражает авторское понимание доминирования. Таким образом, топология диаграммы показывает, какие функции оказывают большее влияние на остальные;
3) неконтекстные диаграммы должны содержать не менее трех и не более шести блоков. Эти ограничения поддерживают сложность диаграмм на уровне, доступном для чтения, понимания и использования. Диаграммы с количеством блоков менее трех вызывают серьезные сомнения в необходимости декомпозиции родительской функции. Диаграммы с количеством блоков более шести сложны для восприятия читателями и вызывают у автора трудности при внесении в нее всех необходимых графических объектов и меток;
4) каждый блок неконтекстной диаграммы получает номер, помещаемый в правом нижнем углу; порядок нумерации – от верхнего левого к нижнему правому блоку (номера от 1 до 6);
5) каждый блок, подвергнутый декомпозиции, должен иметь ссылку на дочернюю диаграмму; ссылка (например, узловой номер, С-номер или номер страницы) помещается под правым нижним углом блока;
6) имена блоков (выполняемых функций) и метки стрелок должны быть уникальными. Если метки стрелок совпадают, это значит, что стрелки отображают тождественные данные;
7) при наличии стрелок со сложной топологией целесообразно повторить метку для удобства ее идентификации;
8) следует обеспечить максимальное расстояние между блоками и поворотами стрелок, а также между блоками и пересечениями стрелок для облегчения чтения диаграммы. Одновременно уменьшается вероятность перепутать две разные стрелки;
|
|
|
9) блоки всегда должны иметь хотя бы одну управляющую и одну выходную стрелку, но могут не иметь входных стрелок;
10) если одни и те же данные служат и для управления, и для входа, вычерчивается только стрелка управления. Этим подчеркивается управляющий характер данных и уменьшается сложность диаграммы;
11) максимально увеличенное расстояние между параллельными стрелками облегчает размещение меток, их чтение и позволяет проследить пути стрелок (рисунок 16);
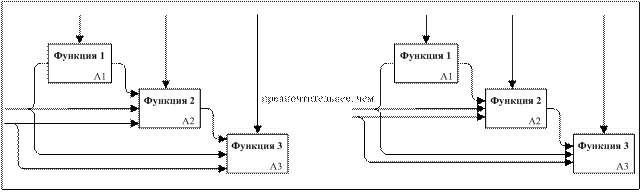
Рисунок 16 – Расстояние между параллельными стрелками
12) стрелки связываются (сливаются), если они представляют сходные данные и их источник не представлен на диаграмме (рисунок 17);

Рисунок 17 – Слияние стрелок
13) обратные связи по управлению должны быть показаны как «вверх и над» (рисунок 9в). Обратные связи по входу должны быть показаны как «вниз и под» (рисунок 9г). Так же показываются обратные связи посредством механизма (рисунок 9д). Таким образом, обеспечивается показ обратной связи при минимальном числе линий и пересечений;
14) циклические обратные связи для одного и того же блока изображаются только для того, чтобы их выделить. Обычно обратную связь изображают на диаграмме, декомпозирующей блок. Однако иногда требуется выделить повторно используемые объекты (рисунок 18);

Рисунок 18 – Циклические обратные связи для одного блока
15) стрелки объединяются, если они имеют общий источник или приёмник, или они представляют связанные данные. Общее название лучше описывает суть данных. Следует минимизировать число стрелок, касающихся каждой стороны блока, если, конечно, природа данных не слишком разнородна (рисунок 19);

Рисунок 19 – Минимизация числа стрелок для каждой стороны блока
16) если возможно, стрелки присоединяются к блокам в одной и той же позиции. Тогда соединение стрелок конкретного типа с блоками будет согласовываться, и чтение диаграммы упростится (рисунок 20);
|
|
|
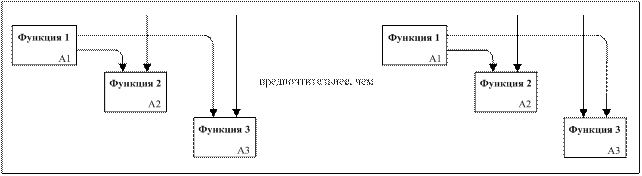
Рисунок 20 – Присоединение стрелок к блокам в одной и той же позиции
17) при соединении большого числа блоков необходимо избегать необязательных пересечений стрелок (рисунок 21). Следует минимизировать число петель и поворотов каждой стрелки (рисунок 22);

Рисунок 21 – Минимизация необязательных пересечений стрелок

Рисунок 22 – Минимизация числа петель и поворотов каждой стрелки
18) блоки (функции) являются сопряжёнными через среду, если они имеют связи с источником, генерирующим данные, без конкретного определения отношения отдельной части данных к какому-либо блоку (рисунок 23а);

а) – сопряжение функций через среду; б) – сопряжение функций через запись
Рисунок 23 – Разновидности сопряжений функции
19) две или более функций являются сопряжёнными через запись, если они связаны с набором данных и не обязательно зависят от того, представлены ли все возможные интерфейсы как сопряжение через среду. Тип интерфейса, показанный на рисунке 23б, предпочтителен, поскольку определяются отношения конкретных элементов данных к каждому блоку;
20) необходимо использовать (где это целесообразно) выразительные возможности ветвящихся стрелок (рисунок 8).
|
|
|


