 |
Прохождение сигнала и шума через измерительный канал
|
|
|
|
С амплитудной модуляцией
Структурная схема одного из 8 измерительных каналов с амплитудной модуляцией (АМ) аппаратуры 8АНЧ-23 приведена на рис. 3.1.
Рис. 3.1. Структурная схема приема АМ сигнала
При тональной АМ на выходе канала в отсутствие шума сигнал на выходе будет иметь вид: 
,
а его эффективное значение равно
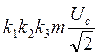, (3.1)
где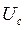 
– амплитуда немодулированного гармонического переносчика (сигнала);
– коэффициент АМ (
).
Мощность шума на выходе измерительного канала
, (3.2)
где 
– спектральная плотность шума 
. Физически есть мощность шума в полосе 
, которая не изменяется во всем диапазоне частот. Коэффициент 2 в (3.2) обусловлен удвоением спектральной плотности шума в детекторе.
С учетом (3.2) эффективное напряжение шума, выделяемое на нагрузке 
, составит
. (3.3)
Определяя эффективное напряжение полезного сигнала через его мощность 
на нагрузке 
из выражений (3.1) и (3.3) и приняв 
, находим относительную среднеквадратическую погрешность в измерительном канале с АМ:
. (3.4)
Заметим, что в формуле (3.4) отсутствуют коэффициенты 
, а также сопротивление нагрузки . Поэтому в дальнейшем при вычислении погрешностей будем принимать 
, 
.
Прохождение сигнала и шума через канал
С частотной модуляцией
Структурная схема приема ЧМ колебаний приведена на рис. 3.2. Под действием шума изменяются амплитуда и частота гармонического переносчика. Изменение амплитуды исключается введением ограничителя.
Рассмотрим компоненту входного шума в полосе 
на частоте 
с амплитудой 
.
 |
Рис. 3.2. Схема приема ЧМ колебаний
Как и ранее, будем считать, что на входе демодулятора ЧМ колебаний напряжение сигнала много больше напряжения шума. Из векторной диаграммы рис. 3.3 найдем
|
|
|
, (3.5)
где 
; (3.6)
при 
из (3.6) получим
, (3.7)
где 
.
 | |||
 | |||
Рис. 3.3. Векторная Рис. 3.4. Спектр шума
диаграмма аддитивной на выходе частотного
смеси сигнала и шума детектора
При изменении 
(рис. 3.3) амплитуда сигнала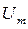 
остается неизменной и равной напряжению ограничения. Будем считать коэффициент передачи ограничителя равным единице. Тогда круговую частоту на выходе частотного детектора (ЧД), настроенного на среднюю частоту 
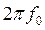, определим как
или
, (3.8)
где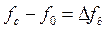 
– девиация частоты, определяет полезный сигнал на выходе ЧД, а оставшаяся часть (3.8) – шумовую компоненту, эффективное напряжение которой в полосе на выходе ЧД равно:
. (3.9)
Как и в детекторе АМ колебаний в ЧД спектральная плотность шума удваивается. Поэтому спектральная плотность шумов на выходе ЧД с учетом (3.8) и (3.9) будет
, (3.10)
т.е. имеем треугольный спектр шума на выходе ЧД. График 
показан на рис. 3.4. Используя (3.10), находим эффективное напряжение в полосе пропускания фильтра НЧ от нуля до 
:
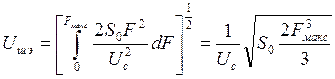. (3.11)
Эффективное напряжение сигнала на выходе ЧД пропорционально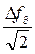 
, где 
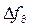– девиация частоты сигнала.
Отношение эффективных напряжений сигнал/шум на выходе фильтра НЧ равно:
, (3.12)
где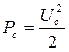 
.
Используя определение индекса модуляции 
в (2.7), из соотношения (3.12) можно найти шумовую относительную среднеквадратическую погрешность для канала с ЧМ:
. (3.13)
Из соотношений (3.4) и (3.13) находим 
.
Это уравнение определяет выигрыш ЧМ в отношении 
по сравнению с АМ. Этот выигрыш обеспечивается за счет более широкой частотной полосы канала с ЧМ, что следует из формул Манаева Е.И. (2.9) и (2.10).
ДИСКРЕТИЗАЦИЯ И КВАНТОВАНИЕ НЕПРЕРЫВНЫХ СООБЩЕНИЙ
Основные понятия и определения
|
|
|
Переход от аналогового представления сигнала к цифровому, который дает в ряде случаев значительные преимущества при передаче, хранении и обработке информации, связан с дискретизацией сигнала 
по времени и с квантованием его по уровню.
Рассмотрим разновидности сигналов, которые описываются функцией .
Непрерывная функция непрерывного аргумента (непрерывный сигнал, рис. 4.1, а). В этом случае функция иаргумент 
принимают непрерывные значения.
Непрерывная функция дискретного аргумента (дискретный во времени сигнал, рис. 4.1, б). Здесь значения функции определяются лишь на дискретном множестве значений аргумента 
.
Дискретная функция непрерывного аргумента (квантованный по уровню сигнал, рис. 4.1, в). В этом случае значения, которые может принимать функция , образуют дискретный ряд чисел 
.
Дискретная функция дискретного аргумента (цифровой сигнал, рис. 4.1, г). Значения, которые могут принимать функция и аргумент , образуют дискретные ряды чисел соответственно и 
.
 |
Рис. 4.1.Виды сигналов: а – непрерывный сигнал; б – дискретный по времени сигнал; в – сигнал, квантованный по уровню; г – цифровой сигнал
Дискретизация состоит в преобразовании сигнала непрерывного аргумента в сигнал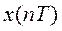 
дискретного аргумента .
Квантование по уровню состоит в преобразовании непрерывного множества значений сигнала 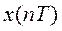в дискретное множество значений 
.
Совместное применение операций дискретизации и квантования позволяет преобразовывать непрерывный сигнал в дискретный по координатам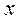 
и .
При квантовании непрерывного сигнала возникает погрешность, обусловленная заменой непрерывных значений сигнала значениями по дискретной шкале уровней (рис. 4.1, г) с ценой деления (шагом квантования) 
, когда истинное значение сигнала представляется ближайшим значением дискретной шкалы.
Максимальное значение этой погрешности, называемой шумом квантования, очевидно, не будет превышать 
.
Шум квантования носит случайный характер, и при большом числе уровней квантования его плотность распределения вероятностей внутри интервала принимается равномерной (рис. 4.2). В этом случае среднеквадратическое напряжение шума квантования определяется как
|
|
|
. (4.1)
Если при получении цифрового сигнала (рис. 4.1, г) пронумеровать дискретные уровни, то каждому значению квантованного сигнала будет соответствовать определенное число. Заранее зная цену деления и номер уровня шкалы, всегда можно восстановить истинное значение уровня квантования и, следовательно, квантованного сигнала. Часто в информационных системах номер уровня квантования представляется в двоичной форме.
При этом будет реализован цифровой сигнал из непрерывного (аналогового) (рис. 4.3, а) с двоичной кодово-импульсной модуляцией (КИМ), получившей широкое применение.
Различают последовательный и параллельный двоичные коды (рис. 4.3, б, в). Последовательный обычно используется в системах (подсистемах) передачи информации, а параллельный – например, на шинах магистрали компьютера.
При передаче (преобразовании) синусоидального сигнала его эффективное напряжение на выходе двоичного канала с КИМ составит 
, где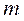 
– число разрядов двоичного кода.
В этом случае шумовая относительная среднеквадратическая погрешность в канале с КИМ с учетом (4.1) составит
. (4.2)
Исходя из структуры сигнала (рис. 4.3) для последовательного двоичного кода: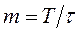 
и необходимой полосы 
частот канала с КИМ: 
(см. раздел 2.10), выражение (4.2) примет вид
. (4.3)
  |
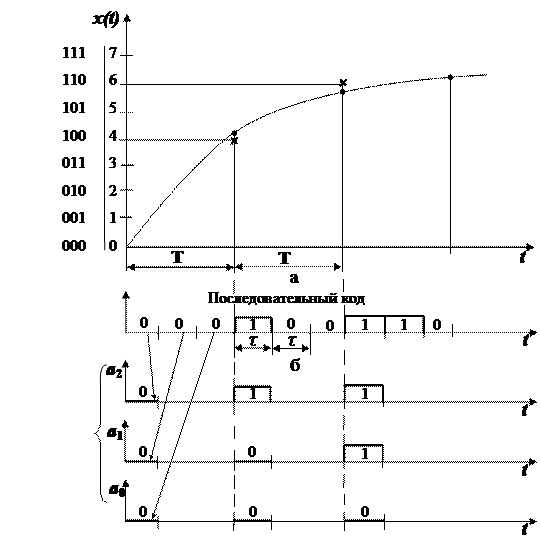в
Рис. 4.3. Кодово-импульсная модуляция
При обработке сигналов дискретизация по времени должна производиться таким образом, чтобы по отсчетным значениям 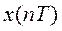можно было получить воспроизводящую функцию 
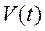,которая с заданной точностью отображает исходную функцию .
Оптимальной является такая дискретизация, которая обеспечивает представление исходного сигнала с заданной точностью при минимальном количестве выборок. В этом случае все отсчеты существенны для восстановления исходного сигнала. При неоптимальной дискретизации, кроме существенных отсчетов, имеются и избыточные отсчеты.
Избыточные отсчеты не нужны для восстановления сигнала с заданной точностью. Они загружают тракт передачи информации, отрицательно сказываются на производительности обработки данных в компьютере, вызывают дополнительные расходы на хранение и регистрацию данных. В связи с этим актуальна задача сокращения избыточных данных. Сокращение избыточной для получателя информации может производиться в процессе дискретизации сигналов. В более общем плане задача сокращения избыточных отсчетов может рассматриваться как задача описания непрерывных сигналов с заданной точностью минимальным числом дискретных характеристик.
|
|
|
|
|
|
