 |
Равномерная дискретизация. Теорема Котельникова
|
|
|
|
В.А. Котельниковым доказана теорема для функций с ограниченным спектром (теорема отсчетов), которая формулируется следующим образом: если наивысшая частота в спектре функции 
меньше, чем 
, то функция полностью определяется последовательностью своих значений в моменты, отстоящие друг от друга не более чем на 
секунд.
Пусть сигнал, описываемый непрерывной функцией времени , имеет ограниченный спектр, т. е. преобразование Фурье
(4.4)
удовлетворяет условию
при 
,
где 
, а 
.
В представлении сигнала интегралом Фурье пределы интегрирования можно ограничить значениями 
:
.(4.5)
Мгновенные значения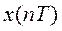 
(рис. 4.1) называются также отсчетами или выборками, являющимися амплитудно-модулированными импульсами (АИМ) с длительностью 
. В этом случае спектр отсчетов 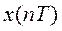будет периодическим с периодом 
.
Спектральную функцию 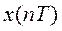можно представить в виде ряда Фурье:
, (4.6)
где коэффициенты разложения
. (4.7)
Сравнивая выражения (4.5) и (4.7), замечаем, что они совпадают с точностью до постоянного множителя 
, если принять 
.
Следовательно
.
Подставив это выражение в формулу (4.6), спектральную функцию запишем в виде
. (4.8)
Подставим выражение (4.8) в формулу (4.5), изменив при этом знак при 
с учетом, что суммирование проводится по всем отрицательным и положительным значениям .Кроме того, учитывая сходимость ряда и интеграла Фурье, изменим порядок операций интегрирования и суммирования:
. (4.9)
После вычисления интеграла
и подстановки полученного результата в формулу (4.9) получим в окончательном виде выражение (4.10):
. (4.10)
В этом выражении 
обозначает интервал между двумя отсчетными точками на оси времени, а 
– выборки (отсчеты) функции в моменты времени 
.
|
|
|
Это выражение показывает, что непрерывная функция с ограниченным спектром может быть точно представлена отсчетами функции 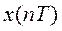, взятыми через равные интервалы
. (4.11)
Как видно из выражения (4.10), непрерывная функция представляется суммой произведений, один из сомножителей которых есть выборка функции, а другой – так называемая функция отсчетов:
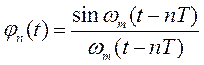, (4.12)
график которой приведен на рис. 4.4.
 |
Рис. 4.4. Функция отсчетов
Свойства функции отсчетов:
а) в точке 
,а в точках 
,где 
– любое целое положительное или отрицательное число, отличное от , 
;
б) спектральная плотность функции 
равномерна в полосе частот и равна 
.
Представление функции рядом Котельникова иллюстрируется рис. 4.5.
 |
Рис. 4.5. Представление сигнала рядом Котельникова
При выводе (4.10) предполагалось, что удовлетворяет условиям Дирихле. Это не дает возможности использовать полученный результат для функций, не стремящихся к нулю при 
, или для функций, не интегрируемых на интервале (а, в).
Теорема Котельникова относится к сигналам с ограниченным спектром. Реальные сообщения имеют конечную длительность. Спектр таких сигналов не ограничен, т. е. реальные сигналы не соответствуют модели сигнала с ограниченным спектром, и применение теоремы Котельникова к реальным сигналам связано с погрешностями при восстановлении сигналов по формуле (4.10) и неопределенностью выбора шага дискретизации (4.11) или частоты отсчетов 
.
Приведенные соображения свидетельствуют, что применение теоремы Котельникова к реальным сигналам вызывает определенные трудности в том случае, если теорема рассматривается как точное утверждение. Для практических условий, однако, идеально точное восстановление функций не требуется, необходимо лишь восстановление с заданной точностью. Поэтому теорему Котельникова можно рассматривать как приближенную для функций с неограниченным спектром.
|
|
|
Практически всегда можно определить наивысшую частоту спектра так, чтобы "хвосты" функции времени, обусловленные отсеканием частот, превышающих ,содержали пренебрежимо малую долю энергии по сравнению с энергией исходного сигнала . Связь практической ширины спектра с учитываемой долей энергии определяется равенством Парсеваля. Квадрат относительной погрешности, вызываемой ограничением спектра частотой , определяется как
|
где 
– полная энергия сигнала ,
– энергия отброшенной части («хвоста») спектра.
При таком допущении для сигнала длительностью 
с полосой частот общее число независимых параметров [т. е. значений 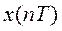], которое необходимо для полного задания сигнала, очевидно, будет
.(4.13)
Число отсчетов 
в данном случае будет наименьшим, что разгружает канал связи и уменьшает необходимый объем памяти при хранении отсчетов.
При этом выражение (4.10) принимает следующий вид (отсчет времени здесь производится от первой выборки):
. (4.14)
Величина представляет собой число степеней свободы сигнала ,так как даже при произвольном выборе значений 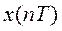сумма вида (4.14) определяет функцию, удовлетворяющую условиям заданного спектра и заданной длительности сигнала.
Параметр 
, который широко применяется в системах передачи информации, называют базой сигнала.
Представление сигналов в виде ряда Котельникова положено в основу построения систем передачи информации с временным уплотнением. Смысл временного уплотнения состоит в том, что в интервале времени между двумя соседними отсчетами одного сигнала можно передавать отсчеты других сигналов. Формирование такого многоканального сигнала показано на рис. 4.6.
 |
Рис. 4.6. Формирование многоканального сигнала в системе при временном уплотнении
Теорема Котельникова лежит в основе импульсных видов модуляции. В частности, период следования импульсов с АИМ1 (2.15) при 
совпадает с периодом отсчетов по Котельникову.
В заключение заметим, что хотя теорема Котельникова базируется на модели сигнала с ограниченным спектром, она имеет большую теоретическую и практическую ценность. Поэтому представление сигналов рядом Котельникова наиболее широко применяется в технике преобразования, передачи и обработки информации.
|
|
|
|
|
|
