 |
Элементы теории приема и обработки информации
|
|
|
|
Общие сведения о приеме сигналов
О передаваемых сигналах обычно имеются некоторые предварительные (априорные) сведения. Могут быть известными, например, частота несущей, вид модуляции и т. п. Сигнал, о котором заранее все известно, не несет информации, а абсолютно неизвестный сигнал нельзя было бы принять.
Известные параметры сигнала используются для лучшего отделения сигналов от помех. Чем больше мы знаем о сигнале, тем совершеннее могут быть методы приема. Параметры, в изменениях которых заключена переносимая информация, называются информационными. Изменения этих параметров в системах передачи информации заранее неизвестны.
В зависимости от вида и назначения системы передачи информации при приеме сигналов возникают следующие основные задачи:
• обнаружение сигналов;
• различение сигналов;
• восстановление сигналов.
При обнаружении сигналов задача сводится к получению ответа на вопрос, имеется на входе приемника сигнал или нет, точнее, имеется ли на входе аддитивная смесь сигнал плюс шум или только шум. С такой задачей мы обычно встречаемся в радиолокации, она также имеет место и в системах передачи дискретной информации. Если мы в состоянии обнаружить сигнал, то появляется возможность передачи информации с помощью двоичного кода. Наличие сигнала (посылка) будет соответствовать символу 1, отсутствие сигнала (пауза) – символу 0. Этот принцип используется в системах с пассивной паузой.
При передаче двух сигналов 
и 
возникает задача не обнаружения, а различения сигналов. Здесь необходимо дать ответ на вопрос: имеется ли на входе приемника сигнал или сигнал ? Ответ на этот вопрос определяется уже не свойствами каждого сигнала в отдельности, а их различием. Сигналы могут отличаться один от другого своими параметрами. Очевидно, нужно стремиться к тому, чтобы различие было наибольшим и устойчивым к воздействию помех. Случай обнаружения может рассматриваться как вырожденный случай различия двух сигналов, когда один из них тождественно равен нулю.
|
|
|
Рассмотрим некоторые из распространенных видов обработки сигналов в системах передачи информации.
Метод накопления
Одним из эффективных и широко применяемых в различных вариантах методов борьбы с помехами является метод накопления. Сущность метода состоит в том, что сигнал или его элементы многократно повторяются. На приеме отдельные образцы сигнала сличаются (обычно суммируются), и так как различные образцы по-разному искажаются помехой в силу независимости последних, то можно восстановить переданный сигнал с большой достоверностью.
В простейшей форме метод накопления часто применяется при телефонном разговоре в условиях плохой слышимости, когда переспрашивают и повторяют одно и то же слово по несколько раз. В случае двоичного кода каждая кодовая комбинация передается по несколько раз. Если вероятность сбоя символов 1 и 0 одинакова, то на приеме решение выносится «по большинству», т. е. воспроизводится символ 1 на данной позиции, когда их число на этой позиции больше числа символов 0, и наоборот, воспроизводится 0, когда число «нулей» больше числа «единиц».
Пример
Переданная комбинация 01001
1-я принятая комбинация 00001
2-я принятая комбинация 11010
3-я принятая комбинация 01101
Воспроизведенная комбинация 01001
Заметим, что можно было бы получить 
образцов сигнала не путем их повторения во времени, а путем передачи по независимым каналам, разделенным по частоте, или каким-либо другим способом.
Существуют и другие разновидности метода накопления. К ним, в частности, относится метод синхронного накопления, когда на протяжении посылки берется не один отсчет, а несколько. На приеме эти отсчеты суммируются в накопителе.
|
|
|
Пусть отдельные отсчеты принятого сигнала:
. (5.1)
Тогда суммы отсчетов с учетом (5.1):
. (5.2)
Величина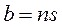 
в выражении (5.2) представляет собой полезный сигнал на выходе приемника. Случайная величина 
представляет собой помеху. Отношение сигнала к помехе на выходе приемника 
равно:
. (5.3)
Заметим, что здесь в отличие от принятых обозначений в главе 3 под отношением сигнала к помехе понимается отношение их мощностей.
Мы полагаем, что 
не коррелированны и имеют одинаковое распределение,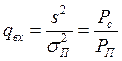 
– отношение сигнала к помехе на входе приемника, 
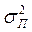– дисперсия случайного процесса.
Таким образом, при описанных условиях накопление отсчетов сигнала (5.3) позволяет увеличить отношение сигнала к помехе на выходе приемника в раз. Суть дела сводится к тому, что мощность сигнала при суммировании растет пропорционально 
(складываются напряжения), а мощность помехи – пропорционально (суммируются мощности). Поэтому отношение сигнала к помехе увеличивается в раз, если отсчеты помехи независимы. При наличии корреляции между значениями помехи этот выигрыш будет меньше.
Метод накопления можно осуществить, беря не сумму отсчетов 
, а интеграл непрерывно изменяющейся функции 
за время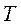 
, равное длительности сигнала:
. (5.4)
Если спектр помехи равномерен в достаточно широкой полосе частот 
, т. е. интервал корреляции помехи 
, то можно показать, что отношение сигнала к помехе на выходе интегратора
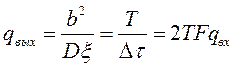. (5.5)
Из выражений (5.4) и (5.5) следует, что выигрыш, получаемый при интегрировании, тем больше, чем больше отношение 
(чем меньше помеха коррелированна с сигналом). Описанный способ приема называется интегральным.
|
|
|
