Пропускная способность.

Непрерывных (аналоговых) каналов

Независимо от характера преобразований сигналов, происходящих в конкретном непрерывном канале связи, можно рассматривать этот канал как некоторый преобразователь (рис. 6.4), устанавливающий соответствие между сигналами на выходе z (t) и на входе y (t). В результате воздействия помех (шумов) соотношение между z (t) и y (t) носит вероятностный характер.

 

 

Рис. 6.4. Структура непрерывного канала

 

Количество информации, содержащейся в случайном сигнале Z_T, о случайном сигнале Y_T находится как

 

I (Z_T, Y_T) = H (Z_T) – H (Z_T/Y_T). (6.16)

 

Рассмотрим случай, когда входной y (t) и выходной z (t) сигналы являются стационарными, эргодическими и стационарно связанными функциями времени. Выберем отрезки этих функций на временном интервале Т, полагая, что вне этого интервала y (t) и z (t) невелики, так что функции y_T (t) и z_T (t) с допустимой погрешностью определяются m отсчетами сигналов, взятыми в соответствии с теоремой Котельникова. В этом случае

 

H (Z_T) = mH (Z),(6.17)

 

H (Z_T/Y_T) = mH (Z/Y),(6.18)

 

в которых H (Z) – энтропия одного отсчета сигнала z_T (t), а Н (Z/Y) – условная энтропия отсчета.

Из выражений (6.16) – (6.18) получаем

 

I (Z, Y) = mH (Z) – mH (Z/Y), (6.19)

 

где индексы опущены, т.к. они отсутствуют в правой части равенства.

При сделанных допущениях скорость передачи информации в непрерывном канале можно определить как

 

, (6.20)

где ; Т ₀ – период отсчетов непрерывных сигналов z_T (t) и y_T (t), определяемый теоремой Котельникова: (здесь F_m – максимальная частота спектра сигналов),

 

, (6.21)

 

. (6.22)

 

Из соотношений (6.20) – (6.22) следует, что скорость передачи информации в непрерывном канале (поток информации, получаемый на выходе канала) зависит от характеристик помех, действующих в канале и определяющих функцию W (z/y), и от статистики передаваемых (преобразуемых) сигналов W (y), т.к. .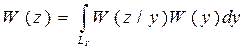

Если W (z/y) определяется свойствами канала, то, варьируя W (y), можно найти такую функцию распределения входного сигнала y (t), при которой поток получаемой информации будет наибольшим. Эти соображения позволяют написать выражение для пропускной способности непрерывного канала в виде соотношения

 

. (6.23)

 

 

Определение пропускной способности

Непрерывного канала

Рассмотрим случай, когда помеха в канале действует как аддитивный шум n (t), т.е.

 

z (t) = y (t) +n (t).

 

Допустим также, что этот шум – стационарный, имеет нормальный закон распределения и его средняя мощность равна его дисперсии P_ш=s_N ² (s_N ² – дисперсия сигнала помехи). Заметим, что шум с нормальным законом распределения обладает максимальной энтропией, и, следовательно, такой шум создает максимальное воздействие на полезный сигнал.

Определив пропускную способность канала, примем во внимание, что его полоса частот пропускания ограничена пределами от 0 до F_m, а средняя мощность Р_c полезного сигнала y (t) выражается через его дисперсию: P_c = s_Y².

С учетом ограничения полосы частот пропускания канала спектры частот сигналов y (t), z (t) и n (t) не должны превышать частоты F_m. В этом случае , и тогда выражение (6.20) можно представить так:

 

.

 

В случае аддитивной помехи последнее выражение можно записать как

 

, (6.24)

 

где H (N) – энтропия источника помехи (в нашем случае) с нормальным законом распределения, имеющим вид

 

. (6.25)

 

Энтропию такого источника найдем по формуле

 

. (6.26)

Так как и , из выражения (6.26) с учетом (6.25) получим

 

(6.27)

 

Пропускную способность рассматриваемого канала можно найти с учетом (6.24) и (6.27) в виде

 

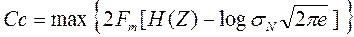. (6.28)

 

Поскольку F_m и s_N в нашем случае заданы, то выражение, стоящее в квадратных скобках, будет наибольшим, если энтропия выходных сигналов канала H (Z) будет максимальной. Так как средние мощности полезного сигнала y (t) и шума n (t) ограничены, то их аддитивная смесь на выходе канала z (t) будет также иметь ограниченную мощность. При таком условии известно, что H(Z) будет наибольшей, если z (t) имеет нормальный закон распределения. Поскольку помеха имеет нормальный закон распределения, то и полезный сигнал y (t) должен иметь нормальный закон распределения. Если полезный сигнал и сигнал помехи статистически независимы, то s_Z ² = s_Y ² + s_N ² и, следовательно,

 

.

 

Подставляя это значение H (Z) в (2.13) и учитывая обозначения s _Y ² =Р_с и s_N ² =Р_ш, получаем

 

.(6.29)

Выражение (6.29) представляет собой широко известную формулу Шеннона. Учитывая важность формулы Шеннона, проводим ее более детальное обсуждение. Из равенства (6.29) следует, что увеличить пропускную способность непрерывного канала можно или за счет расширения его полосы частот пропускания F_m и соответствующего расширения спектра полезного сигнала, или за счет увеличения мощности полезного сигнала Р_с.

Из рассмотрения формулы (6.29) следует, что одно и то же значение пропускной способности можно получить при разных комбинациях значений полосы частот пропускания канала и отношения Р_с /Р_ш.

Рассмотрим два канала: один с полосой частот пропускания от 0 до W ₀ (W ₀= F_м), а другой – от 0 до W > W ₀. При одинаковых пропускных способностях для первого канала отношение мощностей сигнал/шум составит (Р_с /Р_ш)₀, а для второго – Р_с /Р_ш.

С учетом выражения (6.29) и введенных обозначений для рассматриваемых каналов получим

 

, откуда находим

 

.

 

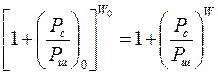Если считать, что шум имеет равномерную спектральную плотность, мощность напряжения шума в полосе частот пропускания первого канала составит Р_ш=S ₀ W ₀, а второго – Р_ш=S ₀ W. Здесь S ₀ характеризует мощность шума в полосе 1 Гц. Тогда предыдущее равенство можно представить в виде

 

. (6.30)

 

На выходе реальных каналов 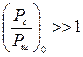. Тогда из (6.30) находим отношение эффективных значений напряжений сигнала и шума:

 

, (6.31)

 

где ,

 

. (6.32)

 

Значение h ² в (6.32) представляет отношение мощности сигнала к удвоенной мощности шума в полосе частот пропускания канала W ₀ или требуемое отношение средней энергии сигнала, связанной с одним отсчетом непрерывного сигнала с максимальной частотой спектра W ₀, к спектральной плотности шума S ₀.

Рассмотрим случай, когда W ®¥. Тогда из (6.31) получим

 

.(6.33)

 

Из (6.33) следует, что минимально возможная требуемая мощность сигнала в идеальном канале с полосой частот пропускания W ₀ определится как

 

.(6.34)

 

Для заданной конечной полосы частот пропускания непрерывного канала W минимально возможная величина h ² _мин может быть определена из выражения (6.31) как

.(6.35)

Ранее отмечалось, что условие максимальной скорости передачи информации обеспечивается в случае, когда источник сообщения имеет нормальный закон распределения. Реальные источники обычно имеют ограниченный диапазон изменения непрерывной случайной величины от -u_c до +u_c.. Наибольшее значение энтропии таких источников дает равномерное распределение. При одинаковой информативности эффективное напряжение источника с равномерным распределением, равное , должно несколько увеличиваться (не более 20 % по сравнению с источником с нормальным распределением).

В реальных каналах обычно в целях простоты рассматривается прохождение гармонических сигналов с амплитудой u_c. Эффективное напряжение гармонического (синусоидального) сигнала составляет . Тогда перерасчет отношения с/ш для гармонического сигнала и сигнала с равномерным распределением будет иметь вид

 

. (6.36)

Заметим, что через отношение выражается относительная шумовая среднеквадратическая погрешность на выходе канала:

. (6.37)

Принимая d = 0,01 () и используя формулы (6.36) и (6.37), находим , а по формуле (6.34) –

 

h²_{мин мин} = ln81,6 = 4,4.

На рис. 6.5 с учетом формулы (6.35) построена зависимость для случая d = 0,01.

 

 

Рис. 6.5. Зависимости для идеального канала

и реальных каналов с АМ и ЧМ

Известно, что в канале с тональной (гармонической) амплитудной модуляцией (АМ) [см. (3.4)]

 

, или, используя (6.32), получим

 

.(6.38)

 

С учетом ширины частотного спектра сигнала в канале при АМ (раздел 2.2) имеем 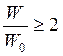. Если 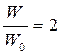, из формулы (6.38) для d_АМ= 0,01 находим h²= 10⁴. Если увеличивать полосу канала, выбирая W >2 W ₀, то мощность шума будет пропорционально возрастать, и для сохранения шумовой погрешности d_АМ= 0,01 необходимо соответственно увеличивать мощность полезного сигнала, а следовательно, и значение h², т.е. зависимость будет линейной (рис. 6.5). Таким образом, увеличение полосы частот пропускания канала с АМ в отличие от идеального канала приводит к ухудшению его энергетических показателей. Поэтому в канале с АМ совершенно нецелесообразно выбирать .

Для канала с частотной модуляцией (ЧМ) с учетом (3.13) и (6.32)

 

(6.39)

 

где - индекс ЧМ,

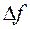- наибольшее отклонение частоты при тональной ЧМ.

Полоса частот пропускания канала с ЧМ по формулам Манаева Е.И. (2.9) и (2.10) в принятых здесь обозначениях определяется как

(6.40)

или

 

.(6.41)

С учетом (6.40) находим

,

 

и тогда формула (6.39) примет вид

.(6.42)

Обычно при ЧМ стараются для снижения шумовой погрешности (6.39) выбирать β >>1. В этом случае из (6.42) получим

.(6.43)

Из формулы (6.43) следует, что с увеличением полосы частот пропускания канала W шумовая погрешность d_ЧМ будет уменьшаться.

Это свойство канала с ЧМ легко объясняется. При увеличении полосы частот пропускания канала для согласования частотного спектра сигнала необходимо повысить индекс ЧМ [см. формулу (6.41)], а увеличение приводит к уменьшению шумовой погрешности d_ЧМ [см. формулу (6.39)].

При заданной погрешности d_ЧМ увеличение полосы частот пропускания канала позволяет уменьшить значение h [см. формулу (6.42)], т.е. снизить значение эффективного напряжения полезного сигнала на входе канала, что отражено для ЧМ на рис. 6.5.

Из сопоставления формул (6.38) и (6.39) при малых значениях 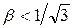канал с ЧМ не имеет преимуществ по шумовой погрешности по сравнению с АМ. Заметим, что при малых значениях полосы частот пропускания каналов с ЧМ и АМ практически одинаковы. На рис. 6.5 качественно приведена зависимость для канала с ЧМ, из которой видно, что в канале с ЧМ более рационально используется расширение полосы частот пропускания, чем в канале с АМ. Однако канал с ЧМ существенно уступает идеальному каналу по Шеннону, особенно при значениях W/W ₀>(W/W ₀ )_опт, когда очень резко появляются так называемые аномальные выбросы шумов. Поэтому при ЧМ оптимальную величину индекса модуляции и минимальную величину h ² выбирают при W_опт. Аномальными выбросами можно пренебречь, если амплитуда несущей в 4 раза больше эффективного напряжения шума в полосе частот пропускания (6.41) канала с ЧМ. При этом вероятность аномальных выбросов составляет . Данному условию соответствует так называемый пороговый сигнал

 

. (6.44)

При нетрудно отыскать с учетом (6.32) и (6.44)

 

. (6.45)

 

Пороговому сигналу (6.45) будет соответствовать (см. рис. 6.5) значение . Для заданной шумовой погрешности (6.39) и с учетом (6.45) будем иметь

 

, откуда

 

, для которого с учетом (6.41) и условия β >>1 находим

 

.

 

Более выгодное использование полосы частот канала обеспечивается в реальных каналах с кодово-импульсной модуляцией (КИМ). Ранее полученное выражение (4.3) для канала с КИМ с учетом теоремы Котельникова примет вид

 

. (6.46)

 

Если ранее отмечалось, что на выходе канала с ЧМ отношение линейно зависит от ширины полосы канала, то при КИМ отношение растет экспоненциально, как в идеальном канале по Шеннону, что подчеркивает достоинство КИМ. Заметим, что в канале с КИМ, как и в канале с ЧМ, имеют место аномальные помехи. Более выгодное использование полосы частот пропускания, аналогичное идеальному каналу, обеспечивается в реальных каналах с кодово-импульсной модуляцией (КИМ).

 

⇐ Предыдущая123456789

Поделиться:

Воспользуйтесь поиском по сайту: