 |
Согласованный фильтр
|
|
|
|
Существует большой класс задач, в которых требуется обнаружить сигнал, если форма его известна. К таким сигналам, в первую очередь, относятся дискретные двоичные сигналы. В этих случаях важным параметром, характеризующим качество обнаружения, является отношение сигнала к помехе. Линейный фильтр, максимизирующий это отношение, называется оптимальным согласованным фильтром.
Пусть на входе фильтра действует сумма сигнала 
и помехи 
, т. е. колебание
.
Полезный сигнал рассматривается не как случайный процесс, а как функция известной формы со спектральной плотностью
,
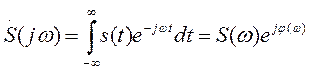где 
и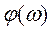 
– амплитудный и фазовый спектры сигнала. Помеху будем считать стационарным случайным процессом типа белого шума с равномерной двухсторонней спектральной плотностью
.
Коэффициент передачи линейного фильтра запишем в виде
.
Сигнал на выходе фильтра, очевидно, равен сумме полезного сигнала 
и помехи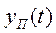 
:
.
Полезный сигнал на выходе можно записать в виде
.
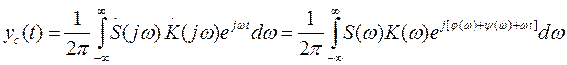Пиковая мощность сигнала в некоторый момент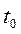 
будет равна:
,
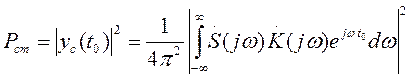а мощность помехи
.
Тогда превышение сигнала над помехой в момент времени 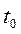будет определяться следующим выражением:
. (5.6)
Необходимо найти, каким должен быть коэффициент передачи фильтра, чтобы отношение сигнала к помехе 
на его выходе было максимальным. Известно неравенство Буняковского - Шварца:
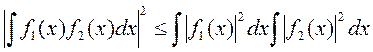. (5.7)
На основании этого неравенства получаем, что при любой характеристике фильтра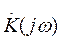 
отношение сигнала к помехе не может превосходить максимального значения:
, (5.8)
где 
– полная энергия сигнала. Указанная в равенстве (5.8) максимальная величина достигается в том случае, когда коэффициент передачи фильтра имеет следующее выражение:
|
|
|
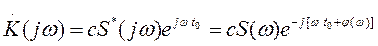, (5.9)
где 
– функция, комплексно сопряженная со спектром сигнала 
; 
– произвольная постоянная.
Выражение (5.9) можно записать в виде двух равенств:
, (5.10)
из которых следует, что амплитудно-частотная характеристика согласованного фильтра с точностью до постоянного множителя совпадает с амплитудным спектром сигнала, а фазочастотная характеристика определяется фазовым спектром сигнала 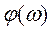и линейной функцией частоты 
. Таким образом, частотная характеристика согласованного фильтра полностью определяется спектром сигнала, "согласована" с ним.
Фаза сигнала на выходе согласованного фильтра с учетом (5.10) будет равна:
.
При 
, т.е. в момент 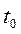, все гармонические составляющие сигнала имеют одинаковую фазу и складываются арифметически, образуя в этот момент пик сигнала на выходе фильтра. Спектральные же составляющие помехи на выходе фильтра имеют случайную фазу. Этим и объясняется доказанное выше положение о том, что согласованный фильтр максимизирует отношение сигнала к помехе на выходе.
В качестве примера рассмотрим построение согласованного фильтра для прямоугольного импульса, заданного в виде:
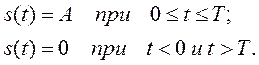
Спектр такого импульса, как известно,
.
На основании (5.9) коэффициент передачи согласованного фильтра будет
. (5.11)
Известно, что умножение на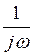 
в частотной области соответствует интегрированию в пределах от 
до 
во временной области, а умножение на 
соответствует задержке сигнала на время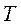 
.
Следовательно, фильтр с коэффициентом передачи (5.11) состоит из интегратора И, включающего в себя дополнительно масштабирующий усилитель с коэффициентом усиления , линии задержки на время Т с коэффициентом передачи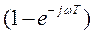 
и вычитающего устройства В (рис. 5.1, а).
 |
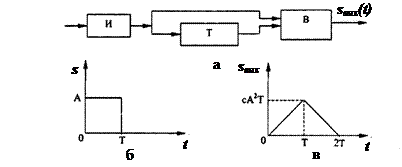Рис. 5.1. Согласованный фильтр для прямоугольного импульса (а), сигнал на его входе (б) и выходе (в)
|
|
|
Сигнал на выходе фильтра имеет форму равнобедренного треугольника (рис. 5.1, в) с основанием 2Т и высотой, равной энергии сигнала сА2Т, т. е.:
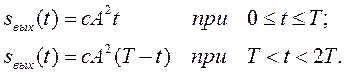
В ряде случаев согласованные фильтры оказываются практически труднореализуемыми. Поэтому часто применяют фильтры, которые согласованы с сигналом только по полосе (квазиоптимальные фильтры). Оптимальная полоса для различных импульсов различна и может быть вычислена без особых трудностей. Так, для фильтра с прямоугольной частотной характеристикой, на который воздействует радиоимпульс прямоугольной формы длительностью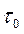 
, оптимальная полоса равна 
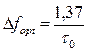. Можно показать, что отношение сигнала к помехе на выходе квазиоптимального фильтра по сравнению с согласованным фильтром уменьшается на величину порядка.
|
|
|
