Проекции отечественных топографических карт

Проекция карт масштабов 1: 25000—1: 500000. Топографические карты масштабов 1:500000 и крупнее составляются в единой равноугольной проекции Гаусса, названной так по имени ее автора (Карл Фридрих Гаусс (1777—1855) - выдающийся немецкий математик и астроном). Эта проекция принята не только для составления карт указанных масштабов, но и для вычисления плоских прямоугольных координат геодезических пунктов. Координаты, вычисленные на плоскости в этой проекции, называются координатами Гаусса.

Геометрическая сущность проекции Гаусса заключается в сле­дующем. Чтобы свести неизбежные искажения проекции к минимуму, не превышающему погрешности графических, построений на картах, поверхность земного эллипсоида делят меридианами, отстоящими друг от друга на 6°, на 60 равных долготных зон (Рис. 20) и каждую из них при вычислении плоских координат и составлении карт развертывают на плоскости независимо от других зон (Рис. 21). Эти зоны называются координатными, так как каждая из них представляет самостоятельную систему плоских прямоуголь­ных координат Гаусса, за начало которой принимается точка пе­ресечения среднего меридиана зоны с экватором.

 

Рис. 20. Деление поверхности земного эллипсоида

На шестиградусные координатные зоны

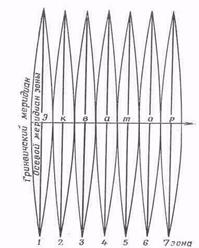
Рис.21 Развертка (изображение) координатных зон на плоскости

Счет зон ведется от Гринвичского меридиана. Зоны развертывают на плоскости таким образом, чтобы сред­ний, так называемый осевой меридиан зоны изображался без искажения его длины прямой линией, перпендикулярной к экватору, который также изображается прямой, но с весьма незначительным искажением (увеличением) длины, присущим про­екции Гаусса. Остальные меридианы и параллели в этой проекции изображаются на плоскости кривыми линиями и тоже с весьма небольшим увеличением их длины. Искажения возрастают по мере удаления от осевого меридиана. Наибольшие искажения по­лучаются на краях зоны. Однако и здесь они, на широтах 30° и выше, не превосходят 0,001 длины измеряемой линии. Искажения же углов не превышают 3' - 4'.

При составлении карт в проекции Гаусса зону разбивают на отдельные листы. Каждый лист карты имеет форму равнобочной трапеции, ограниченной сверху (с северной стороны) и снизу (с южной стороны) параллелями, а с боков - меридианами. На крупномасштабных топографических картах все стороны этих трапеций изображаются прямыми линиями. На картах же мас­штаба 1:100000 и мельче прямолинейны лишь боковые стороны рамок.

Проекция карты масштаба 1:1 000000. Рамки листов этой карты имеют размеры: по долготе 6° (т. е. такие же, как у координатных зон), а по широте 4°, или в линей­ной мере—около 440 км.

Если бы такая карта со столь значительной длиной сторон ра­мок ее листов составлялась в проекции Гаусса, то все четыре сто­роны рамки, т. е. отрезки меридианов и параллелей, разграничи­вающих листы карты, изобразились кривыми линиями. А это исключило бы возможность склеивать листы в блоки. Поэтому карта масштаба 1:100 0000 составляется не в проекции Гаусса, а в одной из произвольных проекций, позволяющей изображать земную поверхность без существенных искажений в пределах каж­дого листа. При этом листы получаются в рамках, допускающих склеивание блоков из нескольких листов (до 9 листов - 2 - 3 ряда по 2 - 3 листа в каждом).

Рис. 22. Разрыв между листами карты масштаба 1:100 0000

Построение карты в этой проекции основано на делении зем­ного эллипсоида не на зоны, как это делается при составлении топографических карт остальных масштабов, а на равнобочные сфероидические трапеции указанных выше размеров, и каждую из них изображают на отдельном листе карты.

В этой проекции изображение всех меридианов, а следова­тельно, и боковых сторон трапеций получается в виде прямых ли­ний, а параллелей - в виде дуг окружностей различных радиусов. Поэтому при склейке вертикальной колонны или горизонтального ряда листов все листы точно совмещаются по смежным сторонам рамок. При склейке же листов, относящихся к разным рядам и колоннам, между ними образуются разрывы, как показано на рис.22. Однако в блоке из 4 - 9 листов эти разрывы незначительны, и их легко устранить при склейке, несколько растягивая бумагу.

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: