 |
Операторы важнейших физических величин
|
|
|
|
6.33 Связь между изображением физических величин операторами и опытом____________
Постулат, устанавливающий связь между изображением физических величин
операторами и опытом ____________________________________________________________
Совокупность собственных значений оператора  ( L1, L2,..., Ln, …) тождественна с совокупностью всех возможных результатов измерений механической величины L, изображаемой оператором
( L1, L2,..., Ln, …) тождественна с совокупностью всех возможных результатов измерений механической величины L, изображаемой оператором  .
.
Иными словами, на опыте наблюдаются только те значения величин: которые совпадают с одним из собственных значений оператора  соответствующего рассматриваемой величине.
соответствующего рассматриваемой величине.
6.34 Операторы координаты и импульса___________________________________________
| Оператор координаты | 
| Оператор координаты частицы есть само число |
| Операторы проекции импульса соответственно на оси х, у, z | 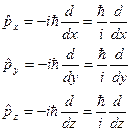
| Операторы координаты проекции импульса являются основными в квантовой теории |
| Оператор вектора импульса | 
| [ 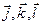 — единичные векторы координатных осей; — единичные векторы координатных осей;
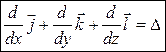 набла - оператор
ла-оператор]
набла - оператор
ла-оператор]
|
6.35 Операторы момента импульса______________________________________________________
| Оператор момента импульса | 
| |
| Операторы проекций момента импульса на оси координат | 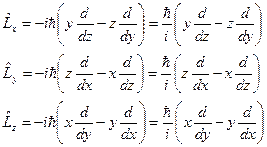
| Расписаны согласно векторному произведению (см. оператор момента импульса) |
Оператор проекции момента импульса на полярную ось г (от нее отсчитывается полярный угол 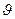 ) )
|

| Вид этого оператора похож на вид операторов проекции импульса 6.34 |
6.36 Уравнения для собственных значений операторов 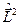 и
и 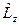 _______________________
_______________________
| Уравнение | Собственные значения | Пояснения |
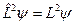
| 
| Лишь при данных собственных значениях квадрата момента импульса решения уравнения удовлетворяют условиям непрерывности, конечности и однозначности (/ — целое положительное число) |
 или
или
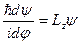
| 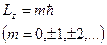
| Решение уравнения имеет вид  . Чтобы функция была однозначной, надо, чтобы . Чтобы функция была однозначной, надо, чтобы 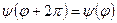 или или 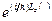 . Это же возможно только тогда, когда Ьг/п = т, где т — нуль или целое (положительное или отрицательное) число . Это же возможно только тогда, когда Ьг/п = т, где т — нуль или целое (положительное или отрицательное) число
|
Вывод. Собственные значения операторов 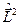 и
и 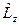 образуют дискретный ряд значений, т. е. момент импульса и проекция момента импульса на произвольную ось г квантуются.
образуют дискретный ряд значений, т. е. момент импульса и проекция момента импульса на произвольную ось г квантуются.
|
|
|
6.37 Операторы энергии____________________________________________________________
Оператор кинетической энергии ____________________________________________________

|  Аналогично, найдя
Аналогично, найдя  и и  , получим оператор кинетической энергии (Δ — оператор Лапласа). , получим оператор кинетической энергии (Δ — оператор Лапласа).
|
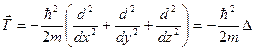
|
Оператор потенциальной энергии ___________________________________________________
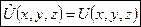 Потенциальная энергия U = U(x,y,z) — функция только координат, поэтому оператор потенциальной энергии есть сама потенциальная энергия.
Потенциальная энергия U = U(x,y,z) — функция только координат, поэтому оператор потенциальной энергии есть сама потенциальная энергия.
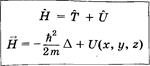 Оператор полной энергии (гамильтониан )__________________________________________
Оператор полной энергии (гамильтониан )__________________________________________
Кинетическая энергия — функция импульсов, а потенциальная — функция координат. По соотношению неопределенностей не существует таких состояний, в которых частицы имели бы одновременно определенные импульсы и координаты. Поэтому полная энергия микрочастицы измеряется как единое целое. В классической механике полную энергию, выраженную через импульсы и координаты, называют функцией Гамильтона Н. Если силы не зависят от времени, то функция Гамильтона совпадает с полной энергией системы: Н = Е.
6.38 Уравнение Шредингера в операторной форме__________________________________
| Уравнение | Обычная запись уравнения | Гамильтониан, оператор полной энергии | Операторная форма |
| Временное уравнение Шредингера | 
| 
| 
|
| Ψ = Ψ(х, у, z, t).Уравнение Шредингера в операторной форме имеет более общий характер и пригодно для описания движения частицы в произвольных стационарных и нестационарных полях, в частности в случае движения частицы в электромагнитном поле | |||
| Стационарное уравнение Шредингера | 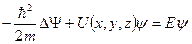
| 
| 
|
[Е — полная энергия частицы; Ψ = Ψ(х, у, z)— координатная часть волновой функции Ψ(x, y, z, t); стационарное уравнение Шредингера в операторной форме имеет регулярные решения лишь при определенных значениях Е, образующих спектр оператора полной энергии]
|
|
|
|
|
|


