 |
Соотношение неопределенностей гейзенберга
|
|
|
|
Во многих случаях классические представления (например, в каждый момент времени частица занимает в пространстве строго определенное 1 место и обладает определенным импульсом) неприменимы для описания микрообъектов. Гейзенберг выдвинул идею о принципиальной невозможности измерения определенных пар связанных между собой характеристик так, чтобы они одновременно имели точные значения.
6.18 Соотношение неопределенностей для координат и импульсов_______
 Микрочастица (микрообъект) не может иметь одновременно точных значений координаты ( х, у, z ) и соответствующих компонентов импульса (
Микрочастица (микрообъект) не может иметь одновременно точных значений координаты ( х, у, z ) и соответствующих компонентов импульса (  ), причем произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка
), причем произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка  .
.
Физический смысл соотношения ____________________________________________
Из соотношения неопределенностей следует, что, например, если микрочастица находится в состоянии с точным значением координаты (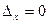 ), то в этом состоянии соответствующая проекция ее импульса оказывается совершенно неопределенной (
), то в этом состоянии соответствующая проекция ее импульса оказывается совершенно неопределенной ( ), и наоборот. Таким образом, для микрочастицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точные значения.
), и наоборот. Таким образом, для микрочастицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точные значения.
6.19 Соотношение неопределенностей для энергии и времени______________
 [
[  — неопределенность энергии некоторого состояния системы;
— неопределенность энергии некоторого состояния системы;  — промежуток времени, в течение которого оно существует]
— промежуток времени, в течение которого оно существует]
Физический смысл соотношения _____________ _________________
Из-за конечности времени жизни атомов в возбужденном состоянии энергия возбужденных состояний атомов не является точно определенной, поэтому частота излученного фотона также должна иметь неопределенность  . Тогда линии спектра должны иметь частоту
. Тогда линии спектра должны иметь частоту  . Опыт действительно показывает, что все спектральные линии размыты.
. Опыт действительно показывает, что все спектральные линии размыты.
|
|
|
6.20 Соотношение неопределенностей — следствие
специфики микрообъектов________________________ _________
Невозможность одновременно точно определить координату и соответствующую проекцию импульса не связана с несовершенством методов измерения или измерительных приборов, а является следствием специфики микрообъектов, отражающей особенности их объективных свойств, а именно двойственной корпускулярно-волновой природы. Соотношение неопределенностей получено при одновременном использовании классических характеристик движения частицы (координаты, импульса) и наличия у нее волновых свойств. Так как в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей является, таким образом, квантовым ограничением применимости классической механики к микрообъектам.
♦ Повышение точности в знании одной переменной, таким образом, ведет к понижению точности в знании другой, и наоборот. Поэтому если в классической механике наличие координат и импульсов (скоростей) системы точно задает ее поведение во времени и пространстве, то предсказание поведения квантовой системы должно носить вероятностный характер.
6.2.3. ВОЛНОВАЯ ФУНКЦИЯ И ЕЕ СТАТИСТИЧЕСКИЙ СМЫСЛ
В общем случае (произвольное движение частицы в произвольных силовых полях) состояние частицы в квантовой механике задается волновой е функцией (или пси-функцией)  , зависящей от координат и времени. Она — основной носитель информации о корпускулярных и волновых свойствах микрочастиц. В частном случае свободного движения частицы волновая функция — плоская волна де Бройля 6.16.
, зависящей от координат и времени. Она — основной носитель информации о корпускулярных и волновых свойствах микрочастиц. В частном случае свободного движения частицы волновая функция — плоская волна де Бройля 6.16.
6.21 Статистическая интерпретация волновой функции_________________
На основании статистической интерпретации вероятность нахождения частицы в момент времени tс координатами х и х + Δ х, у и у + Δ у, г + Δzопределяется интенсивностью волновой функции, т. е. квадратом пси-функции. Поскольку в общем случае Ψ — комплексная функция а вероятность должна быть всегда действительной и положительной величиной, то за меру интенсивности принимается квадрат модуля во волновой функции.
|
|
|
[Ψ* — функция, комплексно сопряженная Ψ]
6.22 Физический смысл Ψ-функции________________________________
 Вероятность А\У нахождения частицы в элементе объем в момент времени I.
Вероятность А\У нахождения частицы в элементе объем в момент времени I.
 Плотность вероятности, т. е. вероятность нахождения частицы в момент времени tв окрестности данной точки пространства. Плотность вероятности — величина, наблюдаемая на опыте, в то время как сама волновая функция, являясь комплексной, наблюдению недоступна. В этом заключается существенное отличие в описании состояний частиц в квантовой и классической механике (в классической механике величины, описывающие состояние частиц, наблюдаемы).
Плотность вероятности, т. е. вероятность нахождения частицы в момент времени tв окрестности данной точки пространства. Плотность вероятности — величина, наблюдаемая на опыте, в то время как сама волновая функция, являясь комплексной, наблюдению недоступна. В этом заключается существенное отличие в описании состояний частиц в квантовой и классической механике (в классической механике величины, описывающие состояние частиц, наблюдаемы).
 Вероятность найти частицу в момент времени tв некотором объеме V.
Вероятность найти частицу в момент времени tв некотором объеме V.
 Условие нормировки вероятностей. Так как
Условие нормировки вероятностей. Так как  dV определяется как вероятность, то, проинтегрировав это выражение в бесконечных пределах, получим вероятность того, что частица в момент времени tнаходится где-то в пространстве. Это есть вероятность достоверного события, а ее в теории вероятностей считают равной 1.
dV определяется как вероятность, то, проинтегрировав это выражение в бесконечных пределах, получим вероятность того, что частица в момент времени tнаходится где-то в пространстве. Это есть вероятность достоверного события, а ее в теории вероятностей считают равной 1.
♦ Волновая функция — объективная характеристика состояния микрочастиц должна удовлетворять ряду ограничений. Она должна быть конечной (вероятность не может быть больше единицы), однозначной (вероятность не может быть неоднозначной величиной) и непрерывной (вероятность не может изменяться скачком)
6.23 Принцип суперпозиции состояний для волновых функций_________
 Если какая-либо система (частица или их совокупность) может находиться в различных состояниях, описываемых волновыми функциями Ψ'1, Ψ2,..., Ψ п,..., то она может находиться в состоянии Ψ, описываемом линейной комбинацией этих функций.
Если какая-либо система (частица или их совокупность) может находиться в различных состояниях, описываемых волновыми функциями Ψ'1, Ψ2,..., Ψ п,..., то она может находиться в состоянии Ψ, описываемом линейной комбинацией этих функций.
[Сп (п = 1, 2,...) — произвольные (в общем случае комплексные) числа, при этом квадрат модуля коэффициента С n, т. е. |Сn|2, равен вероятности обнаружить, что система, представленная состоянием Ψ, может оказаться в состоянии Ψ n. Сложение волновых функций (амплитуд вероятностей), а не вероятностей ( определяемых квадратами модулей волновых функций) принципиально отличает квантовую теорию от классической статистической теории, в которой для независимых событий справедлива теорема сложения вероятностей]
|
|
|
6.2.4. ВРЕМЕННОЕ И СТАЦИОНАРНОЕ УРАВНЕНИЯ ШРЕДИНГЕРА
6.24 Основное уравнение нерелятивистской квантовой механики___________________
Статистическое толкование волн де Бройля 6.22 и соотношение неопределенностей Гейзенберга 6.18 привели к выводу, что уравнением движения в квантовой механике, описывающим движение микрочастиц в различных силовых полях, должно быть уравнение, из которого бы вытекали наблюдаемые на опыте волновые свойства частиц. Основное уравнение должно быть уравнением относительно волновой функции ЧХх, у, г, I), так как именно она, или, точнее, величина Iх?!2, определяет вероятность пребывания частицы в момент времени I в объеме (IV, т. е. в области с координатами х и х + Ах, у иг/ + Ау, гшг + Аг. Так как искомое уравнение должно учитывать волновые свойства частиц, то оно должно быть волновым уравнением, подобно уравнению, описывающему электромагнитные волны.
Временное уравнение Шредингера__________________________________________________

Это уравнение постулируется, а его правильность подтверждается согласием с опытом получаемых с его помощью результатов.
Условия, накладываемые на волновую функцию______________________________________
♦ Волновая функция должна: быть конечной, однозначной и непрерывной.
♦ Производные  —должны быть непрерывны.
—должны быть непрерывны.
♦ Функция |Ψ|2 должна быть интегрируема (это условие сводится к условию нормировки вероятностей 6.22).
♦ Уравнение Шредингера справедливо для нерелятивистских частиц (скорости  υ «с). [
υ «с). [ 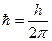 , т — масса частицы, Δ — оператор Лапласа
, т — масса частицы, Δ — оператор Лапласа  , i- мнимая единица, U(x,y,z,t) — потенциальная функция частицы в силовом поле, в котором она движется, Ψ(x,y,z,t) — искомая волновая функция частицы]
, i- мнимая единица, U(x,y,z,t) — потенциальная функция частицы в силовом поле, в котором она движется, Ψ(x,y,z,t) — искомая волновая функция частицы]
6.25 Стационарное уравнение Шредингера________________________________________
Представление волновой функции для стационарных состояний
|
|
|
(состояний с фиксированными значениями энергии)_______________________________
 В случае стационарного силового поля (функция U = U (x,y,z)не зависит от времени и имеет смысл потенциальной энергии) волновая функция представляется в виде произведения двух функций: одна — функция только координат, другая функция — только времени (зависимость от времени выражается множителем
В случае стационарного силового поля (функция U = U (x,y,z)не зависит от времени и имеет смысл потенциальной энергии) волновая функция представляется в виде произведения двух функций: одна — функция только координат, другая функция — только времени (зависимость от времени выражается множителем  )
)
Стационарное уравнение Шредингера____________________________________________
Получилось после подстановки волновой функции во временное уравнение Шредингера и преобразований. 
[Ψ - координатная (амплитудная) часть волновой функции Ψ(x,y,z,t) - ее потенциальная энергия; Δ - оператор Лапласа]

Собственные значения энергии_______________________________________________________
В уравнение Шредингера в качестве параметра входит полная энергия Е. Реальный физический смысл имеют только решения, которые выражаются регулярными функциями Ψ (Ψ должны быть конечными, однозначными и непрерывными вместе со своими первыми производными). Регулярные решения имеют место лишь при определенном наборе Е, отвечающем данной задаче. Эти значения энергии называются собственными. Онимогут образовывать как непрерывный, так и дискретный спектр энергий.
|
|
|


