Движение свободной частицы

Свободная частица — частица, движущаяся в отсутствие внешних полей. Так как на свободную частицу (пусть она движется вдоль оси х) силы не действуют, то потенциальная энергия частицы U (х) = соnst и ее можно принять равной нулю. Тогда полная энергия частицы совпадает с ее кинетической энергией.

6.38 Уравнение Шредингера для стационарных состояний______ ______________________

Уравнение Шредингера _____________________________________ ______________________

 

Ψ (х) = Аe ^iкх = (А = const, к = const);

 

 

♦Зависящая от времени волновая функция Ψ(x, t ) представляет собой монохроматическую волну де Бройля 6.16.

 

Собственные значения энергии ________________________________________________

 

Энергия свободной частицы может принимать любые значения (так
как волновое число kможет принимать любые положительные значения), т. е. энергетический спектр свободной частицы непрерывен.

Плотность вероятности___________________________________________________________

Мера вероятности нахождения частицы в момент времени tв окрестности данной точки пространства. В данном случае плотность веро­ятности не зависит ни от времени, ни от координат: все положения свободной частицы в пространстве равновероятны.

6.2.8. ЧАСТИЦА В ОДНОМЕРНОЙ ПОТЕНЦИАЛЬНОЙ ЯМЕ

С БЕСКОНЕЧНО ВЫСОКИМИ СТЕНКАМИ

6.39 Потенциальная яма с бесконечно высокими стенками_________________________

[ — ширина ямы; энергия отсчитывается от дна ямы; k— волновое число; Е — полная энергия частицы]

6.40 Решение уравнения Шредингера для частицы в яме_____________________________

Граничные условия _______________________________________________________________

Это следует из условия непрерывности. За пределы ямы частица не проникает, и в областях х < 0 и х > I волновая функция Ψ(х) = 0.

Общее решение уравнения Шредингера _____________________________________________

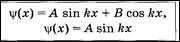Ψ(0) = Ψ() = 0, поэтому В = 0.

Условию Ψ() = А sin k = 0 удовлетворяет

(n = 1,2,3,...).

Собственные функции ____________________________________________________________

А = (коэффициент находится из условия нормировки: )

Нормированные собственные функции _____________________________________________

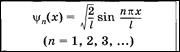Значение п = 0 приводит к тривиальному результату Ψ(x) = 0, а отрицательные значения п — к тем же функциям, но с отрицательным знаком, что не дает новых физических решений.

 

 

 

6.41 Энергетический спектр частицы_______________________________________________

Собственные значения энергии частицы_______________________________________________

Получается из выражений и . Спектр энергии частицы дискретен. Квантованные значения Е_п – уровни энергии, п — квантовое число.

Минимальная, не равная нулю энергия,

соответствующая основному состоянию_______________________________________________

_____________

Наличие отличной от нуля минимальной энергии — следствие соотношения неопределенностей 6.18. Неопределенность импульса (частица «зажата» в яме, следовательно, ее положение известно с неопределенностью 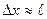). Поэтому энергия нулю не может быть равна (это потребовало бы выполнения условия ).

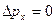♦ Состояние с энергией Е₁— основное состояние, остальные состояния возбужденные. Энергии возбужденных состояний: 4Е₁, 9Е₁, 16Е_1;... (соответственно значениям квантовых чисел п = 2, 3, 4,...) (см. рис. 6.42).

 

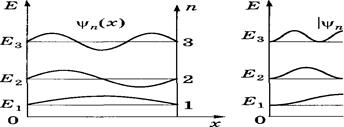
6.42 Собственные функции и плотности вероятности

обнаружения частицы

на разных расстояниях от стенок ямы______________________________________________

 

Из рисунка следует, что, на­пример, в состоянии с п = 2 частица не может находить­ся в центре ямы, в то же вре­мя одинаково часто может пребывать в ее левой и пра­вой частях. Такое поведение частицы указывает на не­состоятельность представ­лений о траекториях частиц в квантовой механике.

 

ОТРАЖЕНИЕ И ПРОХОЖДЕНИЕ

СКВОЗЬ ПРЯМОУГОЛЬНЫЙ ПОТЕНЦИАЛЬНЫЙ ПОРОГ

6.43 Прямоугольный бесконечно протяженный порог______________________________

 

Одномерный потенциальный порог	Потенциальная энергия	Стационарное уравнение Шредингера для одномерного случая

[U₀ — высота потенциального порога; Е — полная энергия частицы; т – масса частицы]

6.44 Энергия частицы больше высоты порога_ (Е > U₀)______________________________

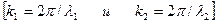— волновые числа; λ ₁ и λ ₂ — соответственно длины волн де Бройля в областях 1 и 2.]

Общие решения уравнений Шредингера ____________________________________________

соответствует плоской волне, распространяющейся в положительном направлении оси х (падающей волне),

— отраженной волне.

Амплитуда падающей волны принята за единицу (А₁ = 1). В области 2 наблюдается только прошедшая волна, поэтому В₂ = 0.

 

♦ О волнах может идти речь после умножения на временной множитель, по­скольку Ψ — координатная часть волновой функции.

6.45 Коэффициенты отражения и прозрачности____________________________________

Коэффициент отражения __________________________________________________________

Равен отношению плотности потока отраженных (п\) частиц к плотнос­ ти потока падающих (n₁) частиц.

 

Коэффициент прозрачности _______________________________________________________

Равен отношению плотности потока прошедших (тг₂) частиц к плотности потока падающих (n₁) частиц.

 

Значения n₁; 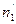; п₂

6.46 Определение R и D для случая Е > U_{0______________________________________________________________}

Коэффициент отражения ___________________________________________________________

 

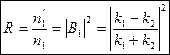
Как п в оптике, R + D= 1. Коэффициент R можно истолковать как вероятность отражения на границе областей, а D— вероятность преодоления потенциального порога. Тогда можно утверждать, что частица либо отразится, либо пройдет в область 2.

Коэффициент прозрачности

 

Вывод. В случае Е > U₀(низкий потенциальный порог) волна частично отражается (коэффициент В₁отличен от нуля) и частично проходит в область 2. В области 2 длина волны де Бройля больше, чем в области 1.

 

 

 

 

Итак, при Е > U ₀ волновое число к₁> к₂ и длина волны λ ₂ > λ.₁.

6.47 Энергия частицы меньше высоты порога ( Е < U₀ ) ________________________________

	Область 1	Область 2
Уравнение Шредингера
Общие решения уравнений Шредингера		При . Однако волновая функция по своему физическому смыссвоему физическому смыслу должна оставаться должна оставаться конечной при всех значени­ях. Следопри всех значениях. Следовательно, нужно принять А2 = 0

 

6.48 Определение коэффициента отражения Rдля случая Е < U₀

Решение уравнений Шредингера	Условия непрерывности	Определение коэффициентовА1 и В1

Коэффициент отражения 6.46_______________________________________________________

 

При Е < U0коэффициент отражения равен единице, т. е. отражение частиц будет полным.

Вероятность найти частицу на единице длины в области 2 _________________________

, т. е. в случае Е < U₀

(высокий прямоугольный потенциальный порог), хотя и наблюдается явление полного отражения, имеется отличная от нуля вероятность найти частицу в области 2, правда, она экспоненциально убывает с уве­личением х. Микрочастица благодаря своим волновым свойствам мо­жет проникать в области, «запрещенные» для классических частиц.

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: