Линейный гармонический осциллятор

Линейный (одномерный) гармонический осциллятор ______________________________

Система, совершающая одномерное движение под действием квазиупругой силы. Задача о гармоническом осцилляторе в квантовой теории играет фундаментальную роль по двум причинам: 1) она встречается во всех задачах, где имеют место квантованные колебания (например, в квантовой теории поля, в теории молекулярных и кристаллических колебаний и т. д.); 2) проблемы, относящиеся к гармоническому осциллятору, — хорошая иллюстрация основных принципов и форм квантовой механики.

6.57 Описание гармонического осциллятора в квантовой механике_________________

Потенциальная энергия линейного гармонического осциллятора ___________________

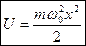Потенциальная яма в данном случае является параболической.

 

Оператор Гамильтона для осциллятора __________________________________________

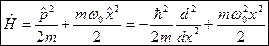6.37

 

 

Стационарное уравнение Шредингера в операторной форме ________________________

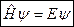Это уравнение по внешнему виду совпадает с записанным выше уравнением 6.38, однако здесь другой оператор.

 

Уравнение Шредингера для гармонического осциллятор а __________________________

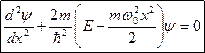Это же уравнение получается при подстановке Uв стационарное уравнение Шредингера 6.25.

 

[ т — масса частицы; ω₀ — собственная частота колебаний осциллятора x - отклонение из положения равновесия; 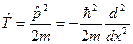— оператор кинетической энергии; — оператор потенциальной энергии; 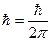- постоянная Планка; Е — полная энергия осциллятора; Ψ — координатная часть волновой функции]

6.58 Следствия уравнения Шредингера для квантового осциллятора________________

Собственные значения энергии __________________________________________________

 

Уравнение Шредингера имеет однозначные, конечные и непрерывные решения только при таких Е_п, т. е. энергия квантового осциллятора может иметь лишь дискретные решения (квантуется).

[ω₀ — собственная частота колебаний осциллятора; 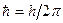— постоянная Планка; Е_п — собственные значения энергии; Е₀ — энергия нулевых колебаний]

Расстояние между соседними уровнями ___________________________________________

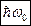Уровни энергии линейного гармонического осциллятора расположены на одинаковых расстояниях друг от друга (на рисунке 6.59 они изображены горизонтальными прямыми)

Энергия нулевых колебаний ___________________________________________________

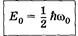Ее существование типично для квантовых систем; следствие соотношения неопределенностей: частица не может находиться на дне потенциальной ямы независимо от ее формы. Если бы это было возможно, то импульс, а также его неопределенность, обращались бы в нуль. Тогда неопределенность координаты , что противоречит пребыванию час­тицы в потенциальной яме.

6.59 Плотности вероятности обнаружения частицы______________________________

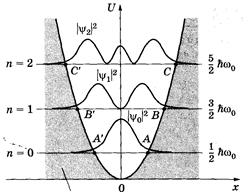Представлены кривые распреде­ления плотности вероятности |\|/_п(х)|² для различных состояний квантового осциллятора (для п = 0, 1 и 2). В точках А и А', Вй В', С и С ^‘потенциальная энергия равна полной энергии (U = Е), причем, как известно, классиче­ский осциллятор не может вый­ти за пределы этих точек. Для квантового осциллятора 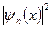и за пределами этих точек имеет конечные значения. Последнее означает, что имеется конечная, хотя и небольшая, вероятность обнаружить частицу за предела­ми потенциальной ямы. Область, запрещенная

Этот результат не противоречит выводам кван­товой классической механикой

механики, так как равенство Т = Е -Uв квантовой механике не имеет силы, поскольку кинетическая (Т) и потенциальная (U) энергии не являются одновременно измеримыми величинами

.

6.60 Плотности вероятности

для квантового и классического осцилляторов___________________________________

На рисунке — кривая распределения При больших значениях п квантовое рас-
плотности вероятности для кванто- пределение плотности вероятности (сплош-
вого (сплошная кривая) и классиче- ная кривая) принимает все большее сход-
ского (пунктир) осциллятора. Поведе- ство с классическим распределением плот-
ние квантового осциллятора значи- ности вероятности (пунктир). В этом про-
тельно отличается от классического является принцип соответствия Бора

Принцип соответствия Бора ______________________________________________ _____

Выводы и законы квантовой механики при больших значениях квантовых чисел должны соответствовать выводам и законам классической физики.

 

 

Уравнения, связывающие корпускулярные свойства (энергия и импульс) и волновые (частота (длина волны)) характеристики микрочастиц _____________________________

Формулы такие же, что и для фотона.

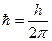[ к — волновое число; постоянная Планка; 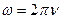циклическая частота]

6. 14 Длина волны де Бройля___________________________________________________

[h— постоянная Планка; р — импульс; т — масса частицы; υ — скорость части­цы; Т — кинетическая энергия частицы; с — скорость распространения света в вакууме; Е — полная энергия частицы]

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: