Формы математического описания дискретных систем

Лабораторная работа

Лабораторная работа № 7

«Анализ дискретной математической модели непрерывного динамического объекта»

7.1. Краткая теория вопроса

Общие сведения

Дискретные системы автоматического управления (САУ), как известно, обладают рядом преимуществ над непрерывными. Вместе с тем, большинство технологических объектов управления (ОУ) являются непрерывными. Совокупность дискретного устройства управления и непрерывного объекта образует дискретно-непрерывную систему. Таким системам присущи все особенности и свойства дискретных систем, но при их проектировании необходимо учитывать свойства непрерывного ОУ, что требует дополнительного анализа.

Для синтеза дискретно-непрерывных систем используется дискретная математическая модель (ММ) непрерывного объекта. Дискретизация выполняется по схеме (рис. 7.1), на которой показаны квантователи (Кл) и экстраполятор (фиксатор) 0-го порядка (Э). На вход системы подается вектор непрерывного сигнала u (t). Квантователь преобразует его в последовательность d-импульсов u[ kT ] (k =0, 1, …) с периодом следования T. Экстраполятор 0-го порядка формирует из d-импульсов ступенчатый сигнал u _Э [ kT ], который подается на вход непрерывного объекта. Такой способ преобразования сигнала называется амплитудно-импульсной модуляцией (АИМ), а квантователь с фиксатором - АИ-модулятором. Реакцией объекта на последовательность входных ступенчатых сигналов является вектор непрерывных выходных сигналов y (t), который подвергается дискретизации выходным квантователем, работающим синхронно с входным. Квантованию также подвергается вектор состояния x (t).

 

 

Рис. 7.1. Переход к дискретной ММ

Формы математического описания дискретных систем

Дискретные ММ связывают входной сигнал u [ kT ] с выходом y[ kT ]. Они имеют три основные формы, аналогичные формам непрерывных ММ: дискретная передаточная функция (ПФ), разностное уравнение «вход-выход» и разностные уравнения в пространстве состояний (ПС).

В основе дискретной передаточной функции используется понятие z-преобразования, которое для непрерывной функции f (t) определяется формулой

.

(7.1)

Преобразование (7.1) получается из формулы дискретного преобразования Лапласа заменой комплексной переменной s на комплексную переменную z:

.

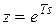(7.2)

Свойства z-преобразования подробно описаны в [1-3]. Некоторые из них приведены ниже.

1. Линейность:

.

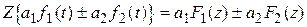2. Сдвиг во временной области:

;

где n > 0, целое.

3. Теорема о предельных значениях:

, если существует.

, если не имеет полюсов на окружности |z|=1 и вне ее.

 

Нахождение дискретной ПФ по известной непрерывной ПФ W (s)выполняется следующим образом. Для непрерывной ПФ объекта с АИ-модулятором

,

(7.3)

где - ПФ экстраполятора 0-го порядка,

z-преобразование можно представить в виде

.

(7.4)

Из (7.4) следует, что сначала нужно по формулам [2] или таблицам [1-3] найти z-преобразование от изображения { W (s) / s }(предварительно разложив на сумму простых дробей), а затем умножить его на (1 - z ^-1).

Переход к разностному уравнению «вход-выход» от дискретной передаточной функции можно выполнить, используя свойство 2. Для этого числитель и знаменатель ПФ записываются в виде полиномов по степеням z ^-1:

.

(7.5)

Отсюда получается разностное уравнение «вход-выход» в обратных разностях, которое удобно записывать для нормированного периода квантования T =1:

.

(7.6)

Переход к разностным уравнениям в ПС выполняется при аналитическом решении системы дифференциальных уравнений непрерывной ММ

(7.7)

на одном периоде квантования. Общее решение системы (7.7) имеет вид

,

(7.8)

где - переходная матрица.

Применяя (7.8) на отрезке 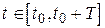, можно записать следующую систему разностных уравнений

(7.9)

где

,

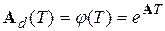(7.10)

с учетом того, что u (t)=const на интервале дискретизации. Матрицы С и D берутся из непрерывной ММ (7.7). Если матрица А неособенная, т. е. , то , где I - единичная матрица.

Переход от дискретной ПФ вида

(7.11)

к разностым уравнениям (7.9) выполняется по той же методике, которая используется для перехода от непрерывной ПФ к системе уравнений в ПС.

Анализ дискретных ММ

В данной работе выполняется сравнительный анализ непрерывной и дискретной ММ по распределению корней, временным и частотным характеристикам. Более подробно методика анализа изложена в литературе [1-3].

Анализ распределения корней позволяет сделать вывод об устойчивости, колебательности и быстродействии объекта. При дискретизации непрерывных объектов нули и полюсы из комплексной s- плоскости переходят в комплексную z -плоскость. Связь между областями s - и z -плоскостей иллюстрируется рис. 7.2.

 

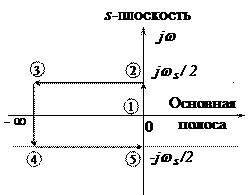Рис. 7.2. Связь между s - и z -плоскостями

Контур в основной полосе частот (здесь - частота квантования), соответствующий устойчивой области непрерывного объекта, преобразуется в единичную окружность z-плоскости. Дискретный объект устойчив, если все его корни находятся внутри единичной окружности z-плоскости.

При переходе от непрерывной ММ к дискретной в некоторых случаях появляются посторонние нули, расположенные на отрицательной части действительной оси z- плоскости (z_d0 на рис. 7.3, б). Они не оказывают влияния на свойства системы и при обратном переходе в непрерывную область исчезают. Остальные корни связаны соотношением (7.2), из которого следует, что действительные и комплексно-сопряженные корни непрерывного объекта на s - и z -плоскостях будут расположены аналогичным образом (рис. 7.3).

 

s -плоскость а)

z -плоскость б)

Рис. 7.3. Распределение нулей и полюсов в s - и z -плоскостях

Анализ во временной области позволяет найти прямые показатели качества системы.

Для нахождения реакции системы, заданной в форме дискретной ПФ, можно использовать обратное z-преобразование от выходного сигнала, равного произведению ПФ и z-преобразования входного воздействия (например, для единичной ступенчатой функции ). Если не требуется получение результата в аналитическом виде, то несколько первых тактов можно найти, сделав разложение z-преобразования выходного сигнала в ряд по степеням z ^-1 (ряд Лорана). Это разложение выполняется делением числителя на знаменатель:

,

(7.12)

где коэффициенты h [ i ] являются значениями временной последовательности с заданным периодом квантования T (см. свойство № 2 z-преобразования).

Для дискретной ММ в ПС существует аналитическое решение, аналогичное формуле Коши для непрерывных систем (7.8):

.

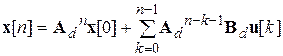(7.13)

Если не требуется аналитическое решение задачи, то вычисление временной последовательности удобно проводить непосредственно по разностным уравнениям «вход-выход» (7.6) и системе в ПС (7.9).

Рис. 7.4. Временные характеристики дискретно-непрерывной системы

Ограничением анализа временных характеристик непрерывных объектов по дискретным ММ является полное отсутствие информации о поведении объекта в промежутках между тактами квантования (рис. 7.4). В работе выполняется моделирование непрерывной части с уменьшенным шагом по времени, что позволяет наблюдать реальную картину динамических процессов.

 

Анализ в частотной области выполняется аналогично непрерывным системам. В дискретной ПФ заменой

,

(7.14)

Рис. 7.5. Амплитудно-частотная A (w) и фазо-частотная j (w) характеристики непрерывной (пунктир) и дискретной ММ

где - частота квантования, - относительная частота (в рад), n =0, ±1, ±2 … - целые числа,

получают выражения для действительной и мнимой частотных характеристик. Анализ (7.14) показывает, что частотные характеристики являются периодическими функциями с периодом по частоте w _s и симметричными относительно w = 0 (рис. 7.5), поэтому их обычно строят при изменении относительной частоты от 0 до p.

 

 

Выбор периода квантования

Из (7.1), (7.10) видно, что коэффициенты дискретных ММ являются функциями от периода квантования T. Следовательно, свойства дискретных моделей зависят от его величины. При обоснованном выборе величины T дискретная ММ сохраняет все основные свойства непрерывного объекта: динамику, устойчивость, управляемость, наблюдаемость.

Однозначных рекомендаций по выбору оптимального периода квантования для каждого конкретного случая не существует, т. к. связь этой величины с требуемыми свойствами зачастую сложна и не может быть выражена аналитически. В таких случаях T является одним из параметров оптимизации САУ численными методами. Некоторые эмпирические соотношения для выбора периода квантования приведены в [2].

Наиболее общую рекомендацию по выбору периода квантования дает теорема В. А. Котельникова [1] (в зарубежной литературе ее называют теоремой Шеннона [2], или импульсной теоремой [3]):

информация о непрерывном сигнале с ограниченным спектром x(t) не будет потеряна, если период квантования

,

(7.15)

где - ширина спектра x(t).

Теорема верна при выполнении двух условий:

1) непрерывный сигнал x (t) обладает финитным спектром, т. е. , если ;

2) на выходе квантователя включен идеальный НЧ-фильтр, имеющий прямоугольную частотную характеристику:

На практике условия теоремы не выполняются: сигналы в сочетании с шумом процесса квантования не могут иметь идеальный финитный спектр, и частотная характеристика фиксатора 0-го порядка также далека от идеальной. Поэтому T из (7.15) выбирается значительно меньшим.

Существуют более грубые ограничения T. При переходе к дискретной ММ должны сохраняться исходные свойства объекта: управляемость и устойчивость (или неустойчивость). Проверить это аналитически можно для ММ не выше 2-го порядка, т. к. это требует нахождения корней полиномов. Наиболее простая оценка соответствия моделей: все корни непрерывного объекта должны находиться в основной полосе частот (рис. 7.2), т. е. для комплексных корне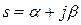й при должно выполняться неравенство , или

.

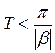(7.16)

Окончательно можно дать следующие рекомендации по выбору T:

1) для разомкнутых дискретно-непрерывных систем необходимо одновременное выполнение условий (7.15) для спектров входного сигнала и помехи и условия (7.16);

2) для замкнутых систем, кроме выполнения рекомендации 1), необходимо учитывать частотные свойства самого объекта, т. к. ступенчатый сигнал на его входе, имеющий бесконечный спектр, проходит на выход и через обратную связь вновь поступает на вход. Так как в процессе синтеза приходится подбирать параметры ОС, а частотные свойства объекта при его замыкании существенно меняются, то рекомендуется выбрать несколько значений T в интервале [ T ₁₎, T_ОУ ], где T ₁₎ - период, выбранный по рекомендации 1), а T_ОУ находится из условия (7.15), где w ₀ - граничная частота спектра объекта, приближенно определяемая по АЧХ. В процессе анализа полученного закона управления выбирается наибольший период T, удовлетворяющий заданному качеству.

12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: