Синтез систем с цифровым ПИД-регулятором

При синтезе непрерывных САУ широко применяются ПИД-регуляторы

,

(8.1)

где K_p, K^*_I и K^*_d - коэффициенты передачи пропорциональной, интегральной и дифференциальной составляющих ПИД-регулятора с несвязными настройками; K_I и K_d - коэффициенты передачи для регулятора со связными настройками.

В цифровых системах используется приближенный аналог ПИД-регулятора. При аппроксимации производной от ошибки выражением

(8.2)

и вычислении интеграла методом трапеций

(8.3)

можно получить следующую дискретную ПФ ПИД-регулятора [3], выполнив z-преобразование (8.2) и (8.3):

(8.4)

Коэффициенты настройки K_p, K_I и K_d ПИД-закона выбираются по логарифмическим ЧХ (ЛЧХ) разомкнутой системы. Из-за того что при выборе структуры регуляторов и корректирующих устройств влияние корней z-плоскости на вид ЛЧХ существенно отличается от непрерывного случая, обычно строят ЛЧХ для билинейного преобразования (w-преобразования) дискретной ПФ [2, 3]. Это позволяет в дискретной области использовать опыт и навыки коррекции непрерывных систем. В данной работе структура ПИД-регулятора задана жестко, а влияние его параметров полностью аналогично непрерывному случаю, поэтому синтез проводится по ЛЧХ, полученным для z-преобразования.

Управление по состоянию

Для ММ в ПС (7.9) закон управления по состоянию имеет вид

,

(8.5)

где K - матрица пропорциональных отрицательных обратных связей (ООС).

Отсюда ММ замкнутой системы принимает вид

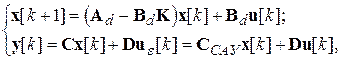
(8.6)

где ; если D = 0, то С _САУ = С.

Структура замкнутой САУ представлена на рис. 8.1, здесь z ^-1 - блок задержки на 1 такт, пунктиром показан перенос узла для перехода к С _САУ.

 

 

Рис. 8.1. Структурная схема САУ с управлением по состоянию

Недостаток данной группы методов состоит в том, что при синтезе не учитывается распределение нулей ОУ, поэтому результаты проявляются только для собственного движения системы, когда u (t)=0 при x (t ₀)¹0. Ясно также, что с помощью пропорциональных ОС нельзя получить систему с реальным астатизмом. Поэтому регуляторы по состоянию комбинируются с регуляторами вынужденного движения, например, с ПИ-регуляторами [3].

Методы этой группы различаются способом вычисления матрицы K.

1) Модальное управление. Ставится задача с помощью пропорциональной ОС по состоянию добиться желаемого распределения полюсов САУ. Задача всегда имеет решение (для одномерных ОУ оно единственное), если пара матриц (A _d, B _d) управляема. Методика задания желаемого распределения полюсов и вычисления матрицы ООС полностью аналогична непрерывным системам [2, 3]. На практике удобно сначала задавать желаемое распределение полюсов в непрерывной области, а затем для заданного периода квантования T делать их пересчет в дискретную область по формуле (7.2).

2) Синтез абсолютно устойчивых систем. Если в качестве желаемого характеристического полинома замкнутой системы выбрать

,

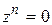(8.7)

где n - порядок ОУ, то полученная система будет иметь нулевые кратные полюсы в дискретной области 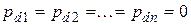, которым соответствуют полюсы в непрерывной области 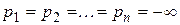, т. е. степень устойчивости системы будет бесконечной. Такие системы называют абсолютно устойчивыми, с апериодическим переходным процессом, с конечным временем установления. Основное их свойство - затухание переходных процессов из произвольного начального состояния x (t ₀)¹0 при u (t)=const за минимально возможное время, n тактов [2, 3]. Это свойство нулевых кратных корней используется также при синтезе дискретных динамических наблюдателей состояния.

3) Оптимальное линейное управление. Для бесконечного интервала времени интегральный квадратичный критерий оптимальности дискретной САУ имеет вид

,

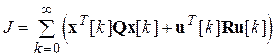(8.8)

где Q [ n ´ n ] - неотрицательно определенная, а R [ m ´ m ] - положительно определенная симметрические матрицы, т. е. , при любых ненулевых x [ k ] и u [ k ]; n - порядок системы; m - число входов.

Управление (8.5) ищется на основании принципа максимума Л. С. Понтрягина из решения дискретного уравнения Риккати [3]

,

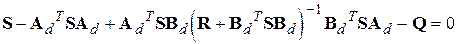(8.9)

где S - решение уравнения (8.9).

Матрица отрицательной обратной связи закона (8.5) равна

.

(8.10)

Необходимым условием существования асимптотически устойчивой оптимальной системы является полная управляемость или стабилизируемость пары (A _d, B _d) с помощью ОС по состоянию, а достаточным - полная наблюдаемость пары (A _d, G), где G - матрица [ n ´ n ] такая, что 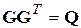[3].

Известной трудностью является выбор элементов матриц Q и R критерия оптимальности (8.8), связанных с требуемыми показателями качества САУ. Доказано, что любое значение квадратичной формы можно получить, задавая ее матрицу в диагональном виде. Обычно требуется задавать критерий оптимальности не для вектора состояния x [ k ], а для вектора выхода y [ k ], размерность которого бывает меньшей. Приравнивая

,

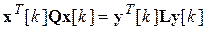(8.11)

с учетом (7.9), можно получить выражение для матрицы Q в виде [2]:

.

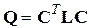(8.12)

Для одномерных САУ матрицы L и R вырождаются в скаляры. Так как для (8.8) имеет значение только их соотношение, то можно произвольно принять значение R=const > 0 и варьировать величину L от 0 до +¥, добиваясь желаемой формы переходного процесса.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: