 |
Тема 1. Радианная мера угла. Поворот точки вокруг начала координат. Формула 1:(радианная →градусная) . Тема 2. Определение тригонометрических функций
|
|
|
|
Тема 1. Радианная мера угла.
Поворот точки вокруг начала координат
Определение: Центральный угол, опирающийся на дугу, длина которой равна радиусу, называется углом в 1 радиан (рад).
 |
Формула 1: ( радианная → градусная)
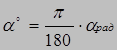
Формула 2: ( градусная → радианная)

Задание 1: Найти радианную меру угла, выраженного в градусах:

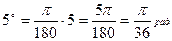
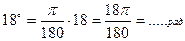
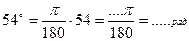

Задание 2: Найти градусную меру угла, выраженного в радианах:

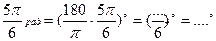


Задание 3: Заполнить таблицу:
| Градусы | 0º | 30º | 45º | 60º | 90º | 120º | 150º | 180º | 270º | 360º |
 радианы радианы
|
 Формула 3:
Формула 3:
l=α ∙ R где l- длина дуги,
R – радиус окружности, которую стягивает дуга
Формула 4:
 S=
S= 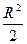 ∙ α, где l- длина дуги,
∙ α, где l- длина дуги,
R – радиус окружности, которую стягивает дуга
S – площадь кругового сектора
α =α рад радианная мера угла
Пример: Решить задачу:
Вычислить длину дуги, если радиус окружности R = 4см, дуга стягивает центральный угол α рад=4, 5рад.
Решение: l=α ∙ R=4, 5∙ 4=18см.
Ответ: l= 18см.
Задание 4: Решить задачи:
1)Вычислить радиус окружности, если её дуга, длиной l=7, 2см стягивает центральный угол α =3, 6рад.
2) Дуга окружности радиуса R=3см стягивает угол α рад=4, 5рад. Найти длину этой дуги l и площадь сектора, ограниченного ею S.
|
|
|
 3) Окружность морских компасов делится на 32 равные дуги, называемые румбами. Вычислите градусную и радианную меры румба.
3) Окружность морских компасов делится на 32 равные дуги, называемые румбами. Вычислите градусную и радианную меры румба.
|
|
|
Задание 5: Заполнить таблицу:
| Угол (в рад. ) | 60º | 45º | ||
 Угол (в град. ) Угол (в град. )
| 
| |||
| Радиус (в см. ) | 
| |||
| Длина дуги (в см. ) | ||||
| Площадь сектора (в см2) | 
|
Поворот точки вокруг начала координат
Определение: Единичной (тригонометрической) окружностью называется окружность с центром в начале координат, радиуса 1.
 |  | ||
Рисунок 1 Рисунок 2
Пример: Точка 1(1; 0) переместилась по окружности на угол 180º против часовой стрелки, а затем на угол 90º по часовой стрелке.
Какие координаты получились? (выполнять по рис/1)
точка. 1(1; 0)=[влево на 180º ]=точка. 3(-1; 0) )=[вправо на 90º ]=точка. 2(0; 1)
Задание 1: Определить координаты точки после перемещения:
· Точка 1(1; 0) переместилась по окружности на 270º против часовой стрелки, затем на 180º по часовой стрелке.
точка. 1 (1; 0)=[влево на 270º ]= точка. 4 (0; -1) )=[вправо на …. ]= точка. …. (...; …)
· Точка 1(1; 0) переместилась по окружности на π против часовой стрелки, затем на 2π по часовой стрелке.
Задание 2: Точка М единичной окружности получена поворотом точки1(1; 0) на угол α. Заполнить таблицу (по рис. 1):
| Угол α | 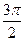
| - 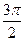
| π | -π | 90º | -90º |
| Координаты т. М | (-1; 0) |  (0; 1) (0; 1)
|
Задание 3: Точка М единичной окружности получена поворотом точки1(1; 0) на угол α. Заполнить таблицу (по рис. 2):
| Угол α | 135º | -15º |  240º 240º
| 400º | -100º | 200º |
| Четверть, в которой расположена т. М | IIч. | IVч. |
Тема 2. Определение тригонометрических функций
Определение 1: Синусом числа α называется ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол α радиан. (sinα )
Определение 2: Косинусом числа α называется абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол α радиан. (cosα )
|
|
|
|

Определение 3: Тангенсом числа α называется отношение синуса числа α к его косинусу. (tgα )
tgα = 
Определение 4: Котангенсом числа α называется отношение косинуса числа α к его синусу. (ctgα )
ctgα = 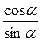
Определение: Функции у=sinα, у=cosα, у=tgα, у=сtgα называют тригонометрическими функциями.

|
 |
Решение:
сosα =  , sinα =
, sinα = 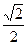 , tgα =
, tgα =  ctgα =
ctgα = 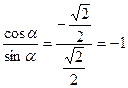
Ответ: сosα =  , sinα =
, sinα = 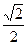 , tgα =-1, ctgα =-1
, tgα =-1, ctgα =-1
Задание 1: По рисунку определить, чему равен sinα, cosα , затем найти tgα, сtgα.
|
 т. М1: т. М2:
т. М1: т. М2:
 сosα =
сosα = 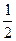 , sinα =…., сosα =…., sinα =….,
, sinα =…., сosα =…., sinα =….,
|
 tgα =
tgα =  tgα =
tgα =  =…..
=…..
ctgα = 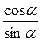 =….. ctgα =
=….. ctgα = 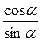 =
=  не сущес- вует, так как на 0 делить нельзя.
не сущес- вует, так как на 0 делить нельзя.
Таблица значений:
| Четверть |  (рад) (рад)
|  (град) (град)
|  (рад) (рад)
|  (град) (град)
| 
| 
| 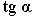
| 
|
| I | 
| 
| не существует | |||||
| I | 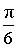
| 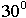
| 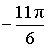
| 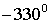
| 
| 
| 
| 
|
| I | 
| 
| 
| 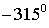
| 
| 
| ||
| I | 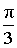
| 
| 
| 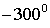
| 
| 
| 
| 
|
| I | 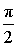
| 
| 
| 
| не существует | |||
| II | 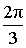
| 
| 
| 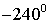
| 
| 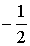
| 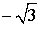
| 
|
| II | 
| 
| 
| 
| 
| 
| -1 | -1 |
| II | 
| 
| 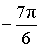
| 
| 
| 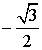
| 
| 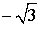
|
| II | 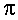
| 
| 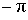
| 
| -1 | не существует | ||
| III | 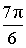
| 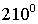
| 
| 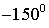
| 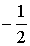
| 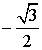
| 
| 
|
| III | 
| 
| 
| 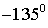
| 
| 
| ||
| III | 
| 
| 
| 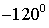
| 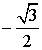
| 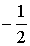
| 
| 
|
| III | 
| 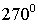
| 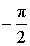
| 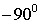
| -1 | не существует | ||
| IV | 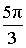
| 
| 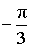
| 
| 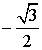
| 
| 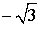
| 
|
| IV | 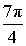
| 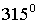
| 
| 
| 
| 
| -1 | -1 |
| IV | 
| 
| 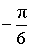
| 
| 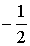
| 
| 
| 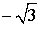
|
| IV | 
| 
| 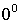
| не существует |
Пример: Вычислить:
3sin 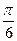 +2cos
+2cos 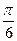 -tg
-tg 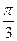 =3∙
=3∙ 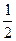 +2∙
+2∙  -
-  =
= 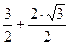 -
-  =
= 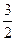 +
+  -
-  =
= 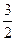
Задание 2: Закончить решение:
·  cos90º -sin90º =0-1=….
cos90º -sin90º =0-1=….
· 4cos π +3ctg  =4∙ (-1)+3∙ 1=….
=4∙ (-1)+3∙ 1=….
· tg 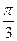 ∙ cos
∙ cos 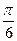 ∙ sin
∙ sin 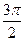 =
=  ∙
∙  ∙ (-1)=….
∙ (-1)=….
· tg45º ∙ sin60º ∙ ctg60º =1∙  ∙ …. =……
∙ …. =……
· 5sin  +3tg
+3tg  -5cos
-5cos  -10ctg
-10ctg  =5∙ ….. +3∙ ……-5∙ ……-10∙ ….. =……
=5∙ ….. +3∙ ……-5∙ ……-10∙ ….. =……
Задание 3: Найти ошибку:
1) 3cos180º +5ctg270º -2sin360º =3∙ 1+5∙ 0=2∙ 1=3+0-2=1
|
|
|
2) 2sin 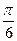 -2cos
-2cos 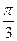 -ctg
-ctg  =2∙
=2∙ 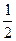 -2∙
-2∙ 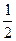 -
-  =1-1-
=1-1-  =-
=- 
 Задание 4: Вычислить и соединить стрелками те примеры, которые имеют одинаковый ответ, ответ выбрать и указать.
Задание 4: Вычислить и соединить стрелками те примеры, которые имеют одинаковый ответ, ответ выбрать и указать.
 |
|
|
|



 .
.
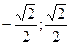 )
)
 )
)