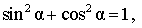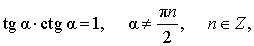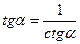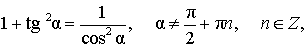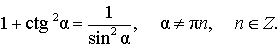 |
Тема 3. Знаки тригонометрических функций
|
|
|
|
Тема 3. Знаки тригонометрических функций
Знаки чисел
определяются тем, в каком квадранте (четверти) координатной плоскости Oxy лежит луч OM (рисунки 1, 2, 3).
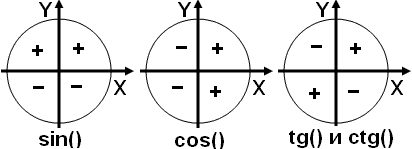
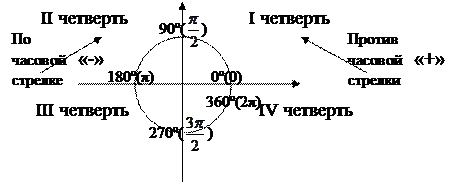
Задание 1: Заполнить таблицу:
| № | функция | четверть | знак |
| sin193º | IIIч. | - | |
| cos(-60º ) | IVч. | ||
| ctg17º | |||
| tg(-100º ) |
Пример: Определить знак произведения
· sin400º ∙ cos215º ∙ tg134º ∙ ctg140º =sin(Iч. )∙ cos(IIIч. )∙ tg(IIч. )∙ ctg(Iч. )=+ ∙ (-) ∙ (-) ∙ + = +
Задание 2: Найти ошибку:
Cos45º ∙ sin(-45º )∙ tg100º ∙ ctg(-100º )=cos(Iч. )∙ sin(Iч. )∙ tg(IIч. )∙ ctg(IIч. )=+ ∙ + ∙ (-) ∙ (-) = +
Задание 3: Определить знак произведения
1) cos370º ∙ tg15º ∙ ctg140º ∙ sin274º
2) sin(-3º )∙ ctg150º ∙ tg300º ∙ cos240º
Тема 4. Зависимость между тригонометрическими
функциями одного и того же аргумента
Задание 1: Заполнить таблицу:
| № | промежуток |  четверть
| Знак sinα | Знак cosα | Знак tgα | Знак ctgα |
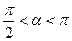
| IIч. | + | - | - | - | |
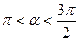
| IIIч. | |||||
| ||||||
|
Формулы:
|
| |||||
| 1(а) | 1(б) | 
|
| ||
|
| |||||
|
| |||||
|
| |||||
| 4(а) | 4(б) |
| 
| ||
|
| |||||
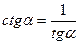
| 5(а) |
| ||||
|
| |||||
| 6(а) |
| ||||
Пример: С помощью основного тригонометрического тождества выяснить, могут ли одновременно выполняться равенства:
Sinα =0, 6 cosα =0, 8
sin2α +cos2α =(0, 6)2+(0, 8)2=0, 36+0, 64= 1 (выполняется)
Задание 2: С помощью основного тригонометрического тождества выяснить, могут ли одновременно выполняться равенства:
 | |||||
 | |||||
 | |||||
|
|
|
Пример: Вычислить cosα, tgα, ctgα, если sinα = 
,
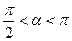
Решение:
| интервал | четверть | Знак sinα | Знак cosα | Знак tgα | Знак ctgα |
|
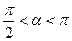
| IIч. | + | - | - | - |
Определим знак:
Формула 1б) 
Формула 2) Формула 3)
tgα =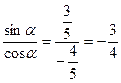 
ctgα =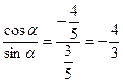 
Ответ: cosα = 
, tgα =-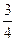 
, ctgα = 
Задание 3: Закончить решение:
1) Вычислить cosα, tgα, ctgα, если sinα =- ,
Решение:
| интервал | четверть | Знак sinα | Знак cosα | Знак tgα | Знак ctgα |
|
| IVч. | - | + | - | - |
Определим знак:
Формула 1б) 
Формула 2) Формула 3)
tgα = 
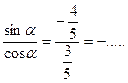ctgα =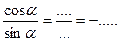 
Ответ: cosα = , tgα =-…, ctgα =-….
2) Вычислить sinα, tgα, ctgα, если cosα =-0, 6,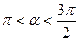
Решение:
| интервал | четверть | Знак sinα | Знак cosα | Знак tgα | Знак ctgα |
|
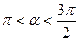
| IIIч. | - | - | + | + |
Определим знак:
Формула 1а) 
Формула 2) Формула 3)
tgα =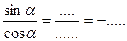 
ctgα =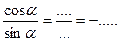
Ответ: sinα =…, tgα =-…, ctgα =-….
Пример: Вычислить sinα, cosα, tgα, , если ctgα =-3,
Решение:
| интервал | четверть | Знак sinα | Знак cosα | Знак tgα | Знак ctgα |
|
| IVч. | - | + | - | - |
Определим знак:
Формула 4а)
Формула 5а)
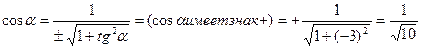
Формула 6а)
Ответ: sinα =- 
, cosα =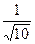 
, tgα =- 
Задание 4: Найти остальные тригонометрические функции, если:
1) sinα =0, 6
2) cosα =- 
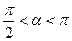
3) tgα =4
| ||
| ||
|
Задание 5: Упростить (по аналогии с решённым):
| № | Упростить | № | Решить самостоятельно |
| 1) |  (1-sinα )∙ (1+sinα )=
=1+sinα -sinα -sin2α =
=1-sin2α =sin2α +cos2α -sin2α =cos2α
| 1) | (1-cosα )∙ (1+cosα ) |
| 2) |  =1+tg2α -1=tg2α
| 2) | Cos2α +sin2α -ctg2α |
| 3) | 
| 3) | 1+tg2α +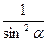 
|
Задание 6: Упростить (воспользоваться формулами: ( а + в )² = а² + 2ав + в²,
|
|
|
( а - в )² = а² - 2ав + в² )
(sinα -cosα )2+(sinα +cosα )2
Задание 7*: Известно, что tgα =8. Найти
1) 
2) 
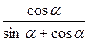
Тема 5. Четность и нечетность тригонометрических функций
Определение: Функция f(х) называется чётной, если для каждого х из области определения этой функции выполняется равенство:
f(-х)=f(х)
Свойство: График чётной функции симметричен относительно оси ординат.
Определение: Функция f(х) называется нечётной, если для каждого х из области определения этой функции выполняется равенство:
f(-х)=-f(х)
Свойство: График нечётной функции симметричен относительно начала координат.
Рассмотрим рисунок
На этом рисунке
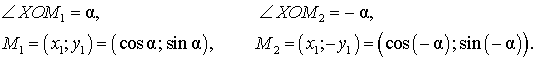
Следовательно, справедливы формулы:
откуда вытекают формулы:
Таким образом, косинус – чётная функция, а синус, тангенс и котангенс – нечётные функции.
cos(-α )=cosα
sin(-α )=-sinα
tg(-α )=-tgα
ctg(-α )=-ctgα
Задание 1: Заполнить таблицу:
| № | функция | упростить | Ответ |
| sin(-90º ) | -sin90º | -1 | |
 tg(-  )
| |||
| cos(-45º ) | |||
ctg(-  )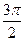
|
Задание 2: Вычислить:
· 2sin(-30º )=-2sin30º =-2∙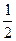 
=-1
· 3tg(-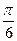 
)=-3tg 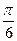=-3∙ ….
· 4cos(- 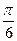)∙ sin(- 
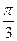)+tg(- )=4∙ 
∙ 
)+(-1)=- 
∙ -1=…..
· 2sin(- 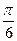)∙ cos(- 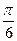)+tg(- 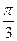)+sin2(- )=…..
Задание 3: Упростить (по аналогии с решённым):
| № |  Упростить
| № | Решить самостоятельно |
| 1) | Sin(-α )∙ cos(-α )∙ tg(-α )=
=-sinα ∙ cosα ∙ (-tgα )=
=sinα ∙ cosα ∙ tgα =
=sinα ∙ cosα ∙  =
=sinα ∙ sinα =sin2α
| 1) | Ctg(-α )∙ sinα +cos(-α ) |
| 2) | (1-sin(-α ))∙ (1-sinα )= =(1+sinα )∙ (1-sinα )= =1+sinα -sinα -sin2α = =1-sin2α =sin2α +cos2α -sin2α =cos2α | 2) | (1+tg(-α ))∙ (1-ctg(-α )) |
Периодичность тригонометрических функций
Определение: Функция f(х) называется периодической, если существует такое число Т≠ 0, что для любого х из области определения этой функции выполняется равенство:
f(х-Т)=f(х)=f(х+Т)
Число Т называют периодом функции f(х).
|
|
|
Рассмотрим рисунок 1, если луч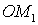 
, повернуть по ходу или против хода часов на полный угол (360 градусов или
радиан), то он совместится с самим собой. Следовательно, справедливы формулы:
а также формулы:
Поворачивая луч 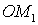на полный угол по ходу или против хода часов n раз ( 
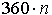градусов или 
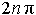радиан), получаем следующие формулы:
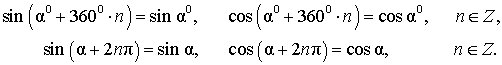
Таким образом, в случае, когда углы измеряются в градусах, периодами синуса и косинуса являются углы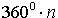 
, 
.
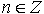В случае, когда углы измеряются в радианах, периодами синуса и косинуса являются числа , .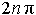
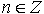В случае, когда углы измеряются в градусах, наименьшим положительным периодом синуса и косинуса является угол 
.
В случае, когда углы измеряются в радианах, наименьшим положительным периодом синуса и косинуса является число .
В случае, когда углы измеряются в градусах, периодами тангенса и котангенса являются углы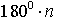 
,
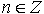
В случае, когда углы измеряются в радианах, периодами тангенса и котангенса являются числа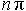 
, .
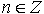В случае, когда углы измеряются в градусах, наименьшим положительным периодом тангенса и котангенса является угол 
.
В случае, когда углы измеряются в радианах, наименьшим положительным периодом тангенса и котангенса являются число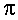 
.
Задание 1: Упростить по образцу:
370º =360º +10º =2π +10º
170º =180º -10º = π -10º
120º =90º 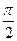+30º = 
+30º
400º =360º -….. =2π -…..
140º =180º -…..
220º =….
135º =…..
|
|
|
