 |
Тема 9.Функция у = sinх, её свойства и график
|
|
|
|
Тема 9. Функция у = sinх, её свойства и график
Основные свойства:
1) Область определения – множество R всех действительных чисел;
2) Множество значений – отрезок[-1; 1];
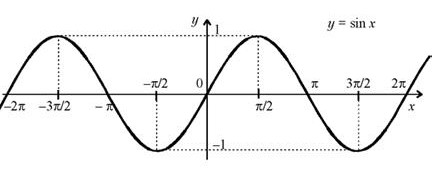
3) Функция у=sinх – периодическая с периодом 2π, т. е. sin(х+2π )=sinх
4) Функция у=sinх - нечётная, т. е. sin(-х)=-sinх
5) Функция у=sinх:
возрастает на отрезках 
убывает на отрезках 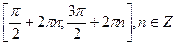
6) Функция у=sinх принимает
Наибольшее значение, равное 1, при х= 
Наименьшее значение, равное –1, при х=- 
Значение равное нулю, при х= 
Задание 1 : Изобразить график функции у=2+sinx
 |
Тема 10. Функция у = cosх, её свойства и график
Основные свойства:
1) Область определения – множество R всех действительных чисел;
2) Множество значений – отрезок[-1; 1];
3) Функция у=cosх – периодическая с периодом 2π, т. е. cos(х+2π )=cosх
4) Функция у=cosх чётная, т. е. cos(-х)=cosх
5) Функция у=cosх:
возрастает на отрезках 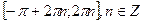
убывает на отрезках 
6) Функция у=cosх принимает
Наибольшее значение, равное 1, при х= 
Наименьшее значение, равное –1, при х= 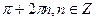
Значение равное нулю, при х= 

Задание 1 : Изобразить график функции у=cos2x
 |
Тема 10. Функция у = tgх, её свойства и график
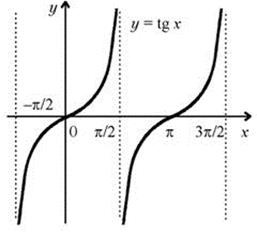 Основные свойства:
Основные свойства:
1) Область определения – множество R всех действительных чисел, кроме чисел  ;
;
2) Множество значений – множество R всех действительных чисел;
3) Функция у=tgх – периодическая с периодом π, т. е. tg(х+π )=tgх
4) Функция у=tgх нечётная, т. е. tg(-х)=-tgх
5) Функция у=tgх возрастает( убывает) на интервалах 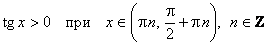 ,
, 
6) Функция у=tgх принимает значение равное нулю, при х= 
Функция у = сtgх, её свойства и график
 Основные свойства:
Основные свойства:
1) Область определения – множество R всех действительных чисел, кроме чисел  ;
;
|
|
|
2) Множество значений – множество R всех действительных чисел;
3) Функция у=сtgх – периодическая с периодом π, т. е. сtg(х+π )=tgх
4) Функция у=сtgх нечётная, т. е. tg(-х)=-tgх
5) Функция у=сtgх возрастает (убывает) на интервалах
 ,
, 
6) Функция у=сtgх принимает значение равное нулю, при х= 
Проверь себя!
1. Вычислить sinα, tgα, cos2α, если cosα =-  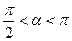
|
| 2. Найти значение выражения: |
| 1)cos135º |
2)sin 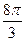
|
3) tg 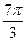
|
4)cos2  -sin2 -sin2 
|
| 3. Доказать тождество: |
| 1) 3cos2α -sin2α +cos2α =2cos2α |
2) 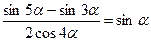
|
| 4. Упростить выражение: |
1)sin(α -β )-sin( 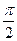 -α )sin(-β ) -α )sin(-β )
|
2)cos2(π -α )-cos2( 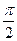 -α ) -α )
|
| 3)2sinα cosβ +cos(α +β ) |
Контрольная работа
Уровень А:
1) Найти значение выражения:
а) cos  +tg
+tg  -sin
-sin 
б) 2cos60º -tg45º
в) 2tg45º +5ctg270º -3sin180º
2) Найти остальные тригонометрические функции, если:
а) sinα =  , 0< α <
, 0< α < 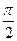
б) cosα =-0, 6, 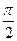 < α < π
< α < π
3) Упростить:
а) sin2α -tgα ∙ ctgα +cos2α
б) 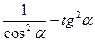
Уровень В:
1) Найти значение выражения:
а) 2cos 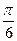 + 4sin
+ 4sin 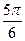 -3ctg
-3ctg 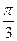
б) cos100º +cos80º
2) Найти остальные тригонометрические функции, если:
а) cosα =-  , π < α <
, π < α < 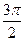
б) ctgα =5, 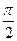 < α < π
< α < π
3) Упростить:
а) (tgα ∙ ctgα +tg2α )∙ sin2α
б) (1-cos2(-α ))∙ (1+tg2(-α ))
Уровень С:
1) Найти значение выражения:
а) sin155º -sin25º
б) sin20º ∙ cos10º +cos20º ∙ sin10º
в) cos20º ∙ cos40º -sin20º ∙ sin40º
2) Найти остальные тригонометрические функции, если tgα =-4, 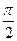 < α < π
< α < π
3) Упростить:
а) 
б) 
в) sin4(-α )+cos2(-α )- cos4(-α )
Подготовка к Единому Государственному экзамену (ЕГЭ)
Прототипы задания В7
Задания по теме «Тригонометрические функции» В ЕГЭ – задачи на преобразование и вычисление тригонометрических выражений. И

|
|

Тренировочная работа №1
Задание В7: Найти значение выражения
|
Выражение |
Ответ | ||||||||||||
 1. 1. 1. 1.
| 1. 1. | | |||||||||||
| 1. 2. | 1. 2. |
| |||||||||||
| 1. 3. | 1. 3. |
| |||||||||||
| 1. 4. | 1. 4. |
| |||||||||||
| 1. 5. | 1. 5. |
| |||||||||||
| 1. 6. | 1. 6. |
| |||||||||||
| 1. 7. | 1. 7. |
| |||||||||||
| 1. 8. | 1. 8. |
| |||||||||||
| 1. 9. | 1. 9. |
| |||||||||||
| 1. 10 | 1. 10 |
| |||||||||||
Тренировочная работа №2
Задание В7: Найти значение выражения
|
|
Ответ | ||||||||||
| 2. 1. | 2. 1. | | |||||||||
| 2. 2. | 2. 2. |
| |||||||||
| 2. 3. | 2. 3. |
| |||||||||
| 2. 4. | 2. 4. |
| |||||||||
| 2. 5. | Найдите значение выражения  , если , если 
| 2. 5. |
| ||||||||
| 2. 6. | 
| 2. 6. |
| ||||||||
| 2. 7. | 2. 7. |
| |||||||||
| 2. 8. | 2. 8. |
| |||||||||
| 2. 9. | 2. 9. |
| |||||||||
| 2. 10 | 2. 10 |
| |||||||||
Учебно – методическое обеспечение дисциплины
Учебники:
ü «Алгебра и начала анализа 10-11 класс» Алимов Ш. А., Колягин Ю. М., Сидоров Ю. В., Шабунин М. И., М: Просвещение;
ü «Алгебра и начала анализа 10класс» Колягин Ю. М., Сидоров Ю. В., Ткачёва М. В., Фёдорова Н. Е., Шабунин М. И., М: Мнемозина;
Дополнительные источники:
Башмаков М. И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.
Башмаков М. И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.
Башмаков М. И. Математика (базовый уровень). 10—11 кл. – М., 2005.
Башмаков М. И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.
Башмаков М. И. Математика: учебник для 10 кл. – М., 2004.
Колмогоров А. Н. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.
Колягин Ю. М. и др. Математика (Книга 1). – М., 2003.
Колягин Ю. М. и др. Математика (Книга 2). – М., 2003.
Луканкин Г. Л., Луканкин А. Г. Математика. Ч. 1: учебное пособие для учреждений начального профессионального образования. – М., 2004.
|
|
|
Пехлецкий И. Д. Математика: учебник. – М., 2003.
Смирнова И. М. Геометрия. 10 (11) кл. – М., 2000.
Интернет-ресурсы:
www. ege66. ru
www. edu. ru
www. uraledu. ru
www. minobraz. ru
www. mathtest. ru
www. allmatematika. ru
www. ega-math. narod. ru
www1. ege. edu. ru/online-testing/math/
www. mathnet. spb. ru
www. exponenta. ru/
 |
|
|
|



 Выражение
Выражение