 |
Тема 6. Формулы сложения. Формулы приведения. Тема 7.Тригонометрические функции двойного и . Тема 8.Преобразование суммы и разности
|
|
|
|
Тема 6. Формулы сложения

cos(α + β ) = cosα ∙ cosβ - sinα ∙ sinβ cos(α - β ) = cosα ∙ cosβ + sinα ∙ sinβ
sin(α + β ) = sinα ∙ cosβ + cosα ∙ sinβ sin(α - β ) = sinα ∙ cosβ - cosα ∙ sinβ
tg(α + β ) = 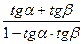
Задание 1: Вычислить по аналогии:

| 1) | Sin73º ∙ cos17º + cos73º ∙ sin17º = = sin(73º + 17º )=sin90º =1 | 1) | Sin73º ∙ cos17º - cos73º ∙ sin17º |
| 2) | cos  ∙ cos ∙ cos  - sin - sin  ∙ sin ∙ sin  =
= cos( =
= cos(  + +  )=cos )=cos  =
=cos2π =1 =
=cos2π =1
| 2) | cos  ∙ cos ∙ cos  + sin + sin  ∙ sin ∙ sin 
|
Задание 2: Упростить:
 1) cos (60° — α ) + cos (60° + α )=
1) cos (60° — α ) + cos (60° + α )=

2) cos (α + π / 6 ) — cos (α — π / 6 )=
Задание 3: Вычислить:
1) Вычислить cos 15°, представив 15° как разность 60° — 45°.

2) Вычислить cos 75°, представив 75° как сумму 30° + 45°.

3) Вычислить cosl05°, представив 105° как сумму 45° + 60°.

Задание 4: Дано: sin α = 0, 6; sin β = —0, 28; 0° < α < 90° и 180°< β < 270°.
Вычислить: 1) cos (α + β );
2) cos (α — β ).

Формулы приведения
Таблица приведения:
| α | 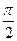 -α -α
| 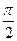 +α +α
| π - α | π + α | 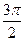 -α -α
| 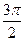 +α +α
| 2π - α | 2π + α |
| sinα | cosα | cosα | sinα | - sinα | - cosα | - cosα | - sinα | sinα |
| cosα | sinα | - sinα | - cosα | - cosα | - sinα | sinα | cosα | cosα |
| tgα | ctgα | - ctgα | - tgα | tgα | ctgα | - ctgα | - tgα | tgα |
| ctgα | tgα | - tgα | - ctgα | ctgα | tgα | - tgα | - ctgα | ctgα |
Пример: Вычислить:
Cos150º =cos(180º -30º )=cos (π -30º )=-cos30º =- 
Sin240º =sin(180º +60º )=sin(π +60º )=-sin60º =- 
Задание 1: Закончить решение:
· 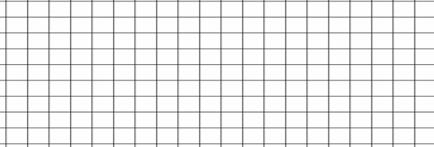 sin135º =sin(90º +45º )=sin(
sin135º =sin(90º +45º )=sin( 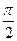 +45º )=cos45º =
+45º )=cos45º = 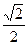
|
|
|
· cos120º =cos(180º -60º )=cos(π -60º )=….
· ctg240º =ctg(270º -30º )=ctg( 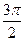 -30º )=…..
-30º )=…..
· sin315º =…..
Задание 2: Найти ошибку:
1) Sin(π – α )∙ cos( 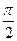 -α )-cos(π – α )∙ sin(
-α )-cos(π – α )∙ sin( 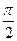 -α )=sinα ∙ sinα -(-cosα )∙ (-cosα )=
-α )=sinα ∙ sinα -(-cosα )∙ (-cosα )=
= sin2α +cos2α =1
2) 
Задание 3: Упростить, из предложенных ответов выбрать верный:
1)  3)
3) 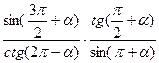
2) 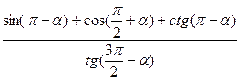 4)
4) 
а) –1 б)ctgα в)  г)1
г)1
Ответ записать в виде таблицы:
| Задание | ||||
| ответ |

 =
=

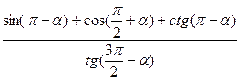 =
=
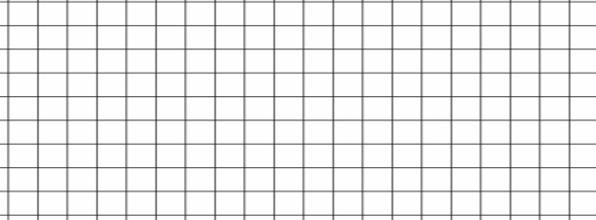
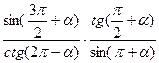 =
=
 =
=
Тема 7. Тригонометрические функции двойного и
половинного аргумента
 |  | ||
sin2α = 2∙ sinα ∙ cosα 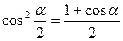
cos2α = cos² α - sin² α 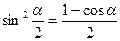
tgα = 
Задание 1: Выразить функции данного аргумента через функции половинного аргумента. Заполнить таблицу:
| № | функция | упростить | формула | ответ |
| sin50º | Sin2∙ 25º | sin2α = 2∙ sinα ∙ cosα | 2∙ sin25º ∙ cos25º | |
 cos36º cos36º
| Cos2∙ 18º | cos2α = cos² α - sin² α | ||
| tg100º | ||||
| Sin8º |
Задание 2: Заполнить таблицу (задание, обратное заданию1):
| № | функция | формула | упростить | ответ |
 2∙ sin15º ∙ cos15º 2∙ sin15º ∙ cos15º
| 2∙ sinα ∙ cosα =sin2α | Sin2∙ 15º | Sin30º = 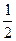
| |
| cos² 75º - sin² 75º | cos² α - sin² α =cos2α | Cos2∙ …º | Cos…º =… | |

|
 Задание 3: Упростить по аналогии:
Задание 3: Упростить по аналогии:
| Sin2α +(sinα -cosα )2= 2∙ sinα ∙ cosα +(sin2α -2∙ sinα ∙ cosα +cos2α )= =2∙ sinα ∙ cosα +sin2α -2∙ sinα ∙ cosα +cos2α = = sin2α +cos2α =1 | 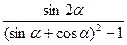 = =
|
Тема 8. Преобразование суммы и разности
тригонометрических функций в произведение
 |
sinα + sinβ = 2∙ sin  ∙ cos
∙ cos 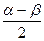 sinα - sinβ = 2∙ sin
sinα - sinβ = 2∙ sin 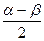 ∙ cos
∙ cos 
|
|
|
cosα + cosβ = 2∙ cos 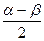 ∙ cos
∙ cos  cosα - cosβ = - 2∙ sin
cosα - cosβ = - 2∙ sin  ∙ sin
∙ sin 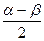
 Задание 1: Вычислить по аналогии:
Задание 1: Вычислить по аналогии:
| 1) | Cos105º +cos75º =
=2∙ cos 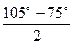 ∙ cos ∙ cos  =
= 2∙ cos 15º ∙ cos 90º =
= 2∙ cos 15º ∙ 0=0 =
= 2∙ cos 15º ∙ cos 90º =
= 2∙ cos 15º ∙ 0=0
| 1) | Sin105º - sin75º |
| 2) | Sin300º + sin60º =
=2∙ sin  ∙ cos ∙ cos 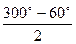 =
= 2∙ sin 180º ∙ cos120º =
=2∙ 0∙ cos120º =0 =
= 2∙ sin 180º ∙ cos120º =
=2∙ 0∙ cos120º =0
| 2) | Cos105º + cos165º |
 Задание 2: Упростить:
Задание 2: Упростить:
1) sin (30° + α ) + sin (30° — α )=
 2) sin( π / 3 + α )— sin( π / 3 — α )=
2) sin( π / 3 + α )— sin( π / 3 — α )=
Задание 3 : Упростить выражения.
1) sin 12° • cos 18° + sin 18° • cos 12°;
2) sin 65° • sin 55° + cos 65° • cos 55°;
3) sin 4, 25 • cos 1, 11 — sin 1, 11 • cos 4, 25;
4) sin 3π /7 • sin 5π /21 — cos 3π /7 • cos 5π /21
5) sin α — sin (α + β ) + cos α • cos (α + β );
6) sin (15° + α ) • cos (15° — α ) + sin (15° — α ) • cos (15° + α ).
Задание 4: Доказать тождества.
1) sin (α + β ) + sin (α — β ) = 2 sin α • cos β;
2) sin (α + β ) — sin (α — β ) = 2cos α • sin β.
3) cos (α — β ) + cos (α + β ) = 2 cos α • cos β;
4) cos (α — β ) — cos (α + β ) = 2 sin α • sin β.
5) sin (α + β ) • sin (α — β ) = sin2 α — sin2 β;
6) cos (α + β ) • cos (α — β ) = cos2 α — sin2 β.
Историческая справка
 Тригонометрические функции (получившие название от греч. trigonon – треугольник и meteo – измеряю) играют огромную роль в математике и ее приложениях.
Тригонометрические функции (получившие название от греч. trigonon – треугольник и meteo – измеряю) играют огромную роль в математике и ее приложениях.
Исследованием тригонометрических функций практически занимались ещё древнегреческие математики, изучая взаимное изменение величин в геометрии и астрономии. Соотношения между сторонами в прямоугольных треугольниках, по своей сути являющиеся тригонометрическими функциями, рассматривались уже в III в. до н. э. в работах Евклида, Архимеда, Аполлония и других ученых.
 Учения о тригонометрических величинах получило развитие в VIII-XV вв. в странах Среднего и Ближнего Востока. Так, в IX в. в Багдаде аль-Хорезми составил первые таблицы синусов. Аль-Бузджани в X в. сформулировал теорему синусов и с её помощью построил таблицу синусов с интервалом 15’, в которой значения синусов приведены с точностью до 8-го десятичного знака. Ахмад-аль-Беруни в XI в. вместо деления радиуса на части при определении значений синуса и косинуса, сделанного до него Птоломеем, начал использовать окружность единичного радиуса. В первой половине XV в. аль-Каши создал тригонометрические таблицы с шагом 1’, которые последующие 250 лет были непревзойдёнными по точности. Самым крупным европейским представителем той эпохи, внесшим вклад в развитие исследования тригонометрических функций, считается Региомонтан.
Учения о тригонометрических величинах получило развитие в VIII-XV вв. в странах Среднего и Ближнего Востока. Так, в IX в. в Багдаде аль-Хорезми составил первые таблицы синусов. Аль-Бузджани в X в. сформулировал теорему синусов и с её помощью построил таблицу синусов с интервалом 15’, в которой значения синусов приведены с точностью до 8-го десятичного знака. Ахмад-аль-Беруни в XI в. вместо деления радиуса на части при определении значений синуса и косинуса, сделанного до него Птоломеем, начал использовать окружность единичного радиуса. В первой половине XV в. аль-Каши создал тригонометрические таблицы с шагом 1’, которые последующие 250 лет были непревзойдёнными по точности. Самым крупным европейским представителем той эпохи, внесшим вклад в развитие исследования тригонометрических функций, считается Региомонтан.
|
|
|
В начале XVII в. в развитии тригонометрии наметилось новое направление – аналитическое. Если до этого учения о тригонометрических функциях строились на геометрической основе, то в XVII-XIX вв. тригонометрия постепенно вошла в состав математического анализа и стала широко использоваться в механике и технике, особенно при рассмотрении колебательных процессов и иных периодических явлений.
О свойствах периодичности тригонометрических функций знал ещё Ф. Виет. Швейцарский математик И. Бернулли (1642-1727) в своих работах начал применять символику тригонометрических функций. Однако близкую к принятой теперь ввел Л. Эйлер в 1748 г. в своей работе «Введение в анализ бесконечных». В ней он рассмотрел вопрос о знаках всех тригонометрических функций любого аргумента.
Тригонометрические функции Эйлер рассматривал как особые числа, называя их общим термином трансцендентные количества, получающиеся из круга.
В 19 в. дальнейшее развитие теории тригонометрических функций было продолжено в работах русского математика Н. Л. Лобачевского (1792-1856), а также в трудах других ученых, например в работах профессоров МГУ Д. Е. Меньшова и Н. К. Бари.
|
|
|


