 |
Классическое симметричное шифрование.
|
|
|
|
Для различных длин текстов и для различных требований к шифрованию разработан ряд режимов.
1) ECB Электронная кодовая книга - обычно применяется для текстов длинной в один блок, при этом все блоки шифруются независимо друг от друга на одном и том же ключе. (в отечественном стандарте ключ простой замены).
Ci = Ek(Pi)
Pi = Dk(Ci)
2) СВС Сцепление блоков шифра.
В этом режиме открытый текст P разбивается на N битные блоки, на следующем шаге первый блок суммируется по модулю два синхропосылкой 2С0, при этом синхропосылка это блок текстат который не несет полезной информации и при этом известен и источнику и приемнику данных, на каждом следующем шаге блок блок текста рассчитывается по формуле:
Ci = Ek(Pi +Ci-1) i от 1 до N
Pi = Ci-1 + Dk
Таким образом если заменить один блок шифротекста изменится расшифрованный блок и следующий за ним.

3) CFB Обратная связь по шифротексту.
Используется блочный шифр генерирующий для источника и приемника псевдослучайную последовательность бит зависящую от ключа и открытого текста. Открытый текст Р разбивается на Т битные блоки. N битный регистр cдвига инициируется значением синхропосылки C0 на каждом шаге Ci = Pi + Ri рассчитывается как сложенное по модулю Pi и Ri, где Ri обозначает Т старших бит шифрограммы функция Ek(Si-1), которые являются псевдослучайной последовательностью.
Регистр сдвига модифицируется следующим образом Т старших бит из Si отбрасывается, а справа присоединяется Сi, при этом Si=St
При расшифровании Si вычисляется по тем же формулам используется в качестве Ri T старших бит расшифрованного текста и открытый текст складывается как зашифрованное по модулю 2
Si = (2^t * Si-1 + Ci)mod2^n 1<=i<=N
Dk(si-1)
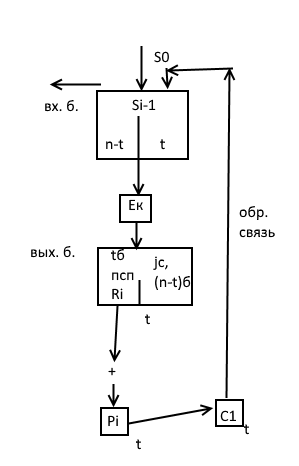
4) OFB Обратная связь по выходу.
|
|
|
Похож на предыдущий, использует блочный шифр для генерации случайной последовательности источником и приемником, переменный размер блока Т и регистр сдвига, инициализируется синхропосылкой на Со, но отличается от предыдущего изменением информации в регистре сдвига.
Si = (2^t *Si-1 +Ri)mod2^n или Si = Ek(Si-1) 1<=i<=N
Кроме того при каждом использовании системы нужно менять синхропосылку т.к. одинаковая синхропосылка генерирует одинаковые псевдослучайные последовательности.
Сравнительная характеристика для более менее распространенных алгоритмов
| Название алгоритма | Размер ключа в битах | Длина блока в битах | Число циклов | Основные операции |
| DES (DES-3) | Подстановка, перестановка, сложение по модулю 2(+) | |||
| ГОСТ 28147-89 | 232,сложение по модулю, подстановки, циклические сдвиги, перестановки | |||
| RCS | 8t, t<=255 | 32-64-128 | До 255 | (+), ЦС, 2длина блока пополам сложение по модулю 2, циклический сдвиг, сложение двух чисел с длинной половины блока |
RSA- разработка конца 70 года, американской безопасностью. Он щас практически стандартизован.
Математическое обоснование метода. Поиск делителей очень большого натурального числа, являющиеся произведением двух чисел задача очень трудоемкая и ограниченная возможностями современной техники.
Рис 6
1. Случайно выбираются два простых* очень больших 250-300 десячичных разрядов числа P.Q.
2. N = p * q
M =(p-1)(q-1)
3. Выбирается небольшое целое нечетное е, взаимно простое с m (не имеющее общих сомножителей) с М.
4. Находится такое D, которое давало бы нам следующую зависимость
(DE)modm = 1.
5. Отправитель шифрует сообщение, при необходимости разбивая его на блоки длинной не более N. Ci = Xi ^ E modn Ci = Xi ^ E modn
Зашифрованное сообщение преобразуется в => 9,1,29
6. Расшифровываем. Pi = Ci ^ D modn.
7. Еn- открытый ключ метода, Dn- закрытый.
Малая теорема ферма позволяет определить является ли число простым.
|
|
|
Для простого числа Р и любого целого К при К<Р справедливо тождество |КР-1| mod p=1
Ассиметричный алгоритм.
| Алгоритм | Описание |
| RSA | Стойкость зависит от сложности факторизации больших целых чисел. |
| Эль-Гамаля | Разновидность алгоритмов Диффи-Хелмана, который можно использовать как для шифрования так и для электронной подписи. На основе (DLP). По заданному простому числу Р основанию G*mod(P) |
| Алгоритмы на эллиптических кривых | Большая производительность, меньшая длинна ключа. Но серьезная математика |
| DSS(DSA) | С реального рынка ушел т.к. нашли слабые места. |
30.10.15
Контроль целостности программный средств и данных осуществляется путём вычисления некоторых характеристик и сравнении их с эталонными значениями. Контрольные характеристики вычисляются при каждом изменении файла по каждому алгоритму.
Метод контрольных сумм().
Под контрольной суммой понимается некоторое значение рассчитанное путём сложения всех чисел из входной последовательности. Если сумма всех входных чисел превышает максимально допустимое значение, заранее заданное для этой величины, то величина контрольной суммы равна остатку от деления итоговой суммы на максимально возможное значение контрольной суммы увеличенное на единицу 1.
CS=T mod (Vmax+1)
ПРИМЕР
36 211 163 4 109 192 58 247 47 92
Сумма всего этого = T= 1159
Если мы считаем что максимальная сумма должна быть величиной в один байт, тогда контрольная сумма равняется
CS = 1159 mod 256=135
|
|
|


