 |
Основные тригонометрические формулы
|
|
|
|
Основные формулы тригонометрии
Перевод градусной меры угла в радианную и обратно. Пусть a° - градусная мера угла, b - радианная, тогда справедливы формулы:

| 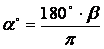
|
Формулы зависимости между функциями одного и того же аргумента.
| 1. | 
| 4. | 
|
| 2. | 
| 5. | 
|
| 3. | 
| 6. | 
|
Формулы сложения.

|

|

|
Формулы двойных и половинных углов.
| 1. | 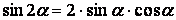
| 5. | 
|
| 2. | 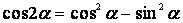
| 6. | 
|
| 3. | 
| 7. | 
|
| 4. | 
| 8. | 
|
Формулы преобразования суммы в произведение.

|
|

| |

| 
|

| 
|
Формулы преобразования произведения в сумму.
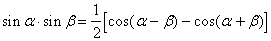
|

|

|
Формулы приведения.
| j | 
| 
| 
| 
| 
| 
| 
| 
| 
|
 j j
| -  a a
|  a a
|  a a
|  a a
| -  a a
| -  a a
| -  a a
| -  a a
|  a a
|
 j j
|  a a
|  a a
| -  a a
| -  a a
| -  a a
| -  a a
|  a a
|  a a
|  a a
|
 j j
| -  a a
|  a a
| -  a a
| -  a a
|  a a
|  a a
| -  a a
| -  a a
|  a a
|
 j j
| -  a a
|  a a
| -  a a
| -  a a
|  a a
|  a a
| -  a a
| -  a a
|  a a
|
Решение простейших тригонометрических уравнений
| Уравнение | Общее решение | Частные случаи | ||

| 
| 
| ||
 , ,

| 
| 
|
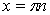
| 
|
 , ,

| 
|

| 
|

|
 , ,

| 
| 
|
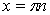
| 
|
 , ,

| 
| 
| 
| 
|
Для решения простейших тригонометрических неравенств 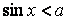 ,
,  ,
,  ,
,  (вместо знака
(вместо знака  могут стоять
могут стоять 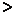 ,
, 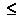 ,
, 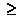 ) применяют графический способ. Находят точки пересечения графика соответствующей функции с прямой
) применяют графический способ. Находят точки пересечения графика соответствующей функции с прямой  , расположенные ближе к началу координат, и затем используют периодичность функции.
, расположенные ближе к началу координат, и затем используют периодичность функции.
Для решения более сложных тригонометрических неравенств их сводят к простейшим случаям с помощью упрощений. Графики и основные свойства тригонометрических функций.
|
| 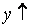 для для 
| ||
 для для 
| |||
 для для 
| |||
 для для 
| |||
| | |||
|
| 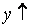 для для 
| ||
 для для 
| |||
 для для 
| |||
 для для 
| |||
| | |||
|
| 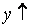 для для 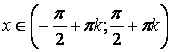
| ||
 для для 
| |||
 для для 
| |||
| | |||
|
|  для для 
| ||
 для для 
| |||
 для для 
| |||
|
| |||
Графики и основные свойства обратных тригонометрических функций.
|
| 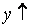 для для 
|
 для для 
| |
 для для 
| |
| Функция нечетная | |
| | |
|
|  для для 
|
 для для 
| |
 для для 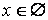
| |
| Функция ни четная, ни нечетная | |
| | |
|
| 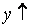 для для 
|
 для для 
| |
 для для 
| |
| Функция нечетная | |
| | |
|
|  для для 
|
 для для 
| |
 для для 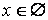
| |
| Функция ни четная, ни нечетная | |
| | |
Примеры решения задач.
1.  Найти значение следующих тригонометрических выражений:
Найти значение следующих тригонометрических выражений:
 ,
, 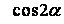
 , если
, если  .
.
Решение. Выпишем формулы для нахождения  ,
, 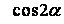
 :
:
 ,
,  ,
,  .
.
 .
.
Из основного тригонометрического тождества найдем  :
:


Далее найдем значения искомых выражений:


Ответ:  ,
, 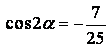 ,
, 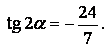
2.  Доказать тождество:
Доказать тождество:
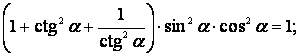
Решение. Приведем левую часть к 1:

 .
.
Тождество доказано.
3.  Вычислить значение выражения:
Вычислить значение выражения:

Решение. Используя формулы приведения, получим:

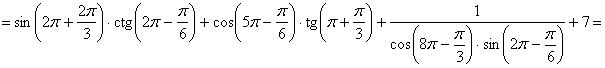

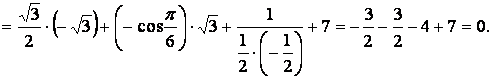
Итак, значение выражения 0.
 Пояснения к разделу: Решение тригонометрических уравнений и неравенств.
Пояснения к разделу: Решение тригонометрических уравнений и неравенств.
Для решения произвольных тригонометрических уравнений и неравенств применяют те же основные приемы, которые были описаны ранее для решения алгебраических уравнений: введение новой переменной и разложение на множители левой части уравнения или неравенства.
1. Уравнения, однородные относительно 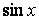 и
и  .
.
Каждое из уравнений:
 ,
,
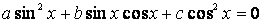 и т.д.
и т.д.
называется однородным относительно 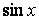 и
и  . Сумма показателей степеней у
. Сумма показателей степеней у 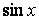 и
и  во всех членах такого уравнения одинакова. Эта сумма называется степенью однородного уравнения. Делением на
во всех членах такого уравнения одинакова. Эта сумма называется степенью однородного уравнения. Делением на  ,
,  степень однородного уравнения, оно приводится к уравнению, алгебраическому относительно
степень однородного уравнения, оно приводится к уравнению, алгебраическому относительно  .
.
Разделив, например, уравнение 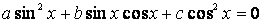 на
на  , получим уравнение:
, получим уравнение:
 .
.
При  эти уравнения эквивалентны, так как если
эти уравнения эквивалентны, так как если  , то из первого уравнения получим, что и
, то из первого уравнения получим, что и  , что невозможно (
, что невозможно ( 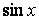 и
и  при одном и том же аргументе в нуль не обращаются). Далее из эквивалентного уравнения находим
при одном и том же аргументе в нуль не обращаются). Далее из эквивалентного уравнения находим  , решая квадратное уравнение относительно
, решая квадратное уравнение относительно  , а по значениям
, а по значениям  - соответствующие значения
- соответствующие значения  .
.
|
|
|
4.  Решить уравнение:
Решить уравнение:

Решение. Заменяя  и
и  , получим однородное уравнение:
, получим однородное уравнение:  ,
,
Или  .
.
Деля на  (
(  ), получим:
), получим:
 .
.
Вводим новую переменную 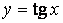 и получаем квадратное уравнение относительно нее:
и получаем квадратное уравнение относительно нее:
 .
.
Корни этого уравнения:  . Далее получаем равносильную совокупность уравнений:
. Далее получаем равносильную совокупность уравнений:


 2. Уравнения, левая часть которых раскладывается на множители, а правая часть равна нулю.
2. Уравнения, левая часть которых раскладывается на множители, а правая часть равна нулю.
Перенеся все члены любого уравнения в левую часть, его можно привести к виду  .
.
Если левая часть этого уравнения раскладывается на сомножители, то каждый из них приравнивается к нулю, и уравнение распадается на несколько простых уравнений. Очень важно при этом иметь в виду, что корнями первоначального уравнения будут только те из корней полученных уравнений, которые входят в область определения первоначального уравнения.
5.  Решить уравнение:
Решить уравнение:
 .
.
Решение. Здесь целесообразно использовать формулы преобразования произведения тригонометрических функций в сумму. Воспользовавшись этими формулами, получим уравнение:

или  .
.
Разность косинусов преобразуем в произведение  , которое равносильно совокупности уравнений:
, которое равносильно совокупности уравнений:


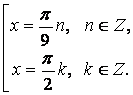
 3. Уравнения вида
3. Уравнения вида  .
.
Эти уравнения можно решать при помощи универсальной тригонометрической подстановки  , воспользовавшись формулами, выражающими
, воспользовавшись формулами, выражающими 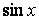 и
и  через
через  :
:
 и
и  .
.
Исходное уравнение сводится к дробно-рациональному алгебраическому уравнению, решение которого нами было рассмотрено ранее.
Такие уравнения рациональнее решать введением вспомогательного угла:  . Рассмотрим дальнейший ход решения уравнения путем эквивалентных преобразований левой части:
. Рассмотрим дальнейший ход решения уравнения путем эквивалентных преобразований левой части:
 .
.
Введем обозначения:
 и
и 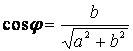 .
.
Заметим, что выражение в скобках в этом случае преобразуется в косинус разности аргументов:
 .
.
Таким образом, исходное уравнение приводится к эквивалентному простейшему тригонометрическому уравнению:
 , или
, или  ,
,
решение которого, суть


 ,
,  .
.
Задача решена в общем виде.
|
|
|
6.  Решить уравнение:
Решить уравнение:
 .
.
Решение. (первый способ) Заменив 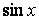 и
и  через
через  , получим:
, получим:

 .
.
Введем новую переменную:  и получим эквивалентное квадратное уравнение относительно
и получим эквивалентное квадратное уравнение относительно 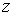 :
:
 ,
,
у которого дискриминант равен нулю и, следовательно, имеем единственный корень  . Задача свелась к решению уравнения:
. Задача свелась к решению уравнения:
 ;
;  ;
;  ,
,  .
.
Решение. (второй способ). Введем вспомогательный угол:  .
.
Тогда решение исходного уравнения сразу запишется в виде:


 =
= 
 ,
,  .
.
Иными словами, мы получили тот же ответ, что не удивительно.
|
|
|





 ,
,  ,
,  , период
, период  , нечетная
, нечетная
 ,
, 
 ,
,  , период
, период  , нечетная
, нечетная
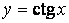 ,
,  ,
, 
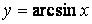 ,
,  ,
,  , непериодическая функция
, непериодическая функция
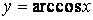 ,
,  , непериодическая функция
, непериодическая функция
 ,
,  , непериодическая функция
, непериодическая функция
 ,
,  , непериодическая функция
, непериодическая функция