 |
Простейшие тригонометрические неравенства
|
|
|
|
Простейшими тригонометрическими неравенствами называются неравенства вида:
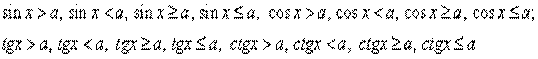
Тригонометрические неравенства могут быть решены по следующему общему правилу:
1. Найти область допустимых значений неизвестной (ОДЗ).
2. Записать соответствующее уравнение, заменив знак неравенства знаком равенства.
3. Решить уравнение, полученное в предыдущем пункте.
4. На числовой оси отметить ОДЗ, корнями уравнения разбить ОДЗ на промежутки.
5. На каждом интервале выбрать одну пробную точку и подставить ее в исходное неравенство. Если неравенство выполняется, то данный интервал необходимо включить в ответ. Если неравенство не выполняется, то интервал следует исключить из рассмотрения.
1. Сделать отбор характерных для неравенства точек – корней уравнения и концов промежутков ОДЗ. Если исходное неравенство нестрогое, то корни уравнения следует записать в ответ, в противном случае – отбросить. Концы промежутков ОДЗ проверить подстановкой в исходное неравенство. Подходящие из них включить в ответ.
Пример. Решить неравенство 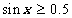 .
.
Решение. Нарисуем единичную окружность и отметим на ней точки, для которых ордината превосходит 0.5 (жирная синяя линия).
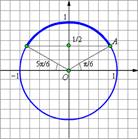
Решим данное неравенство на промежутке длины равной наименьшему периоду функции y= 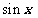 . Для
. Для 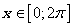 решением неравенства будут
решением неравенства будут 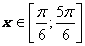 . Следовательно, все решения неравенства запишутся в виде
. Следовательно, все решения неравенства запишутся в виде 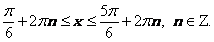
Для решения неравенств с тангенсом и котангенсом полезно использовать линии тангенсов и котангенсов. Таковыми являются прямые x = 1 и y = 1, соответственно, касающиеся единичной окружности.

Легко заметить, что если построить луч с началом в начале координат, составляющий угол α с положительным направлением оси абсцисс, то длина отрезка от точки (1;0) до точки пересечения этого луча с линией тангенсов в точности равна тангенсу угла, который составляет этот луч с осью абсцисс. Аналогичное наблюдение имеет место и для котангенса
|
|
|
Пример. Решите неравенство 
Решение. Сделаем замену 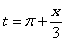 . Неравенство примет вид
. Неравенство примет вид  . Решим полученное неравенство на промежутке длины равной наименьшему периоду функции y=
. Решим полученное неравенство на промежутке длины равной наименьшему периоду функции y=  , а именно на промежутке
, а именно на промежутке 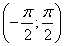 . С помощью линии тангенсов устанавливаем
. С помощью линии тангенсов устанавливаем 
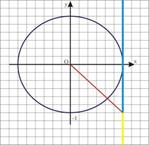
Следовательно, решение неравенства  можно записать в виде
можно записать в виде  . Возвращаясь к переменной x, получаем
. Возвращаясь к переменной x, получаем
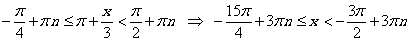 .
.
Ответ: 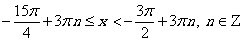 .
.
Упражнения для самостоятельной работы.

 1)
1)  ,
,
2)  ,
,
 3)
3)  ,
,
 4)
4) 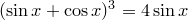 ,
,
 5)
5) 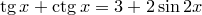 ,
,
 6)
6)  ,
,
 7)
7)  .
.
8) Решите уравнения
 9)
9)  ,
,
 10)
10)  .
.


 ,
,
11)  ,
,
Решите тригонометрические неравенства
 12)
12)  ,
,
 13)
13) 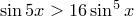 ,
,
 14)
14) 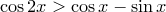 ,
,
 15)
15) 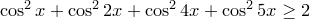 .
.
Список литературы
1.Пехлецкий И. Д. Математика, СПО. - М.: Академия, 2013.
2.Григорьев С.Г., Задулина С.В. Математика, СПО. - М.: Академия, 2014.
3.Спирина М.С., Спирин П.А. Теория вероятностей и математическая статистика, СПО. - М.: Академия, 2014.
4.Валуце И.И., Дилигул Г.Д. Математика для техникумов. - М.: Наука, 2014.
5.Подольский В. А., Суходский А.М. Сборник задач по высшей математике. - М.: Высшая школа, 194.
6.Башмаков М.И. Математика, 10 кл. - М.: Академия, 2013.
7.Башмаков М.И. Математика, 11 кл. - М.: Академия, 2013.
ПРАКТИЧЕСКАЯ РАБОТА № 4
«Функции, их свойства и графики»
Цели урока:
1) Обобщить теоретические знания по теме: «Функции, свойства и графики».
2) Рассмотреть алгоритмы решений заданий теме «Функции, свойства и графики», решить задачи.
3) Формировать умение самоконтроля, рассудительность, терпение, самостоятельность.
Теоретический материал
График линейной функции
Линейная функция задается уравнением 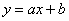 . График линейной функций представляет собой прямую. Для того, чтобы построить прямую достаточно знать две точки.
. График линейной функций представляет собой прямую. Для того, чтобы построить прямую достаточно знать две точки.
Пример 1
Построить график функции  . Найдем две точки. В качестве одной из точек выгодно выбрать ноль.
. Найдем две точки. В качестве одной из точек выгодно выбрать ноль.
|
|
|
Если 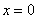 , то
, то 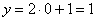
Берем еще какую-нибудь точку, например, 1.
Если  , то
, то 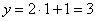
При оформлении заданий координаты точек обычно сводятся в таблицу:
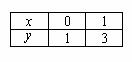
А сами значения рассчитываются устно или на черновике, калькуляторе.
Две точки найдены, выполним чертеж:

При оформлении чертежа всегда подписываем графики.
Не лишним будет вспомнить частные случаи линейной функции:

|
|
|


