 |
Тема исследовательской работы «Э кспертные оценки рисков и страхования»
|
|
|
|
Ход работы
Справка
Формула полной вероятности
Формула Байеса
Формула условной вероятности
1.4 Разбор решения практической задачи по теме варианта
Выполнение теста
Самостоятельная работа
- Справка
1.1 Формула полной вероятности
Допустим, что проводится опыт, об условиях которого можно заранее сделать взаимо исключающие друг друга предположения (гипотезы):
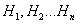
Мы предполагаем, что имеет место либо гипотеза 
, либо 
… либо 
. Вероятности этих гипотез известны и равны:
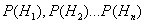
Тогда имеет место формула полной вероятности:
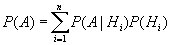
Вероятность наступления события А равна сумме произведений вероятности наступления А при каждой гипотезе на вероятность этой гипотезы.
1.2 Формула Байеса
Она позволяет пересчитывать вероятность гипотез в свете новой информации, которую дал результат А. Формула Байеса в известном смысле является обратной к формуле полной вероятности.
Условная вероятность
У словной вероятностью 
(два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.
Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.
В частности, отсюда получаем:
Рассмотрим следующие практические задачи.
Задача № 1. Предположим, произошла авиакатастрофа и эксперты заняты исследованием ее причин. Заранее известны 4 причины, по которым произошла катастрофа: либо причина , либо , либо 
, либо 
. По имеющейся статистике эти причины имеют следующие вероятности:
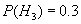
При осмотре места катастрофы найдены следы воспламенения горючего, согласно статистике вероятность этого события при тех или иных причинах такая:
|
|
|
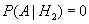
Вопрос: какая причина катастрофы наиболее вероятна?
Вычислим вероятности причин при условия наступления события А.
Отсюда видно, что наиболее вероятной является первая причина, так как ее вероятность максимальна.
Задача № 2. Страховая компания занимается страхованием жизни. 10% застрахованных в этой компании являются курильщиками. Если застрахованный не курит, вероятность его смерти на протяжении года равна 0.01 Если же он курильщик, то эта вероятность равна 0.05.
Какова доля курильщиков среди тех застрахованных, которые умерли в течение года?
Варианты ответов: (А) 5%, (Б) 20%, (В) 36 %, (Г) 56%, (Д) 90%.
Решение
Введём события:
- = {застрахованный – курильщик}
- = {застрахованный – не курильщик}
-
= {застрахованный умер в течение года}
Условие задачи означает, что
Кроме того, поскольку события и образуют полную группу попарно несовместимых событий, то 
.
Интересующая нас вероятность – это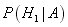 
.
Используя формулу Байеса, мы имеем:
,
поэтому верным является вариант (В).
Выполнение теста.
Самостоятельная работа.
Задача 4.
Рассмотрим посадку самолета в аэропорту. При посадке погодные условия могут быть такими: низкой облачности нет (), низкая облачность есть (). В первом случае вероятность благополучной посадки равна P1. Во втором случае – Р2. Ясно, что P1>P2.
Приборы, обеспечивающие слепую посадку, имеют вероятность безотказной работы Р. Если есть низкая облачность и приборы слепой посадки отказали, вероятность удачного приземления равна Р3, причем Р3<Р2. Известно, что для данного аэродрома доля дней в году с низкой облачностью равна 
.
Найти вероятность благополучной посадки самолета.
Задача 2.
Страховая компания продаёт договора страхования жизни трёх категорий: стандартные, привилегированные и ультрапривилегированные.
50% всех застрахованных являются стандартными, 40% - привилегированными и 10% - ультрапривилегированными.
Вероятность смерти в течение года для стандартного застрахованного равна 0.010, для привилегированного – 0.005, а для ультра привилегированного – 0.001.
|
|
|
Чему равна вероятность того, что умерший застрахованный является ультрапривилегированным?
Вариант.
|
|
|
