 |
Тема исследовательской работы «Парадокс Монти Холла»
|
|
|
|
Ход работы
Справка
Формула полной вероятности
Формула Байеса
Формула условной вероятности
1.4 Разбор решения практической задачи по теме варианта
Выполнение теста
Самостоятельная работа
- Справка.
1.1 Формула полной вероятности
Допустим, что проводится опыт, об условиях которого можно заранее сделать взаимо исключающие друг друга предположения (гипотезы):
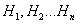
Мы предполагаем, что имеет место либо гипотеза 
, либо 
… либо 
. Вероятности этих гипотез известны и равны:
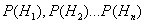
Тогда имеет место формула полной вероятности:
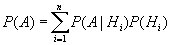
Вероятность наступления события А равна сумме произведений вероятности наступления А при каждой гипотезе на вероятность этой гипотезы.
1.2 Формула Байеса
Она позволяет пересчитывать вероятность гипотез в свете новой информации, которую дал результат А. Формула Байеса в известном смысле является обратной к формуле полной вероятности.
Условная вероятность
У словной вероятностью 
(два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.
Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.
.
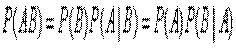В частности, отсюда получаем:
Рассмотрим следующую практическую задачу
Задача № 1
Студент из 20 билетов подготовил к экзамену 12. Студент взял билет, к которому он не подготовился. Преподаватель в виде исключения разрешил взять второй билет. Какова вероятность того, что студенту во второй попытке достанется один из подготовленных билетов.
|
|
|
Решение.
Обозначим событие «студент взял билет, к которому он не подготовился» через A. Обозначим событие «студенту достанется во второй попытке один из подготовленных билетов» через B.
Обозначим событие (А×В/A) – взять первый билет, к которому он не подготовился, и второй из подготовленных билетов при условии, что, что первое событие уже произошло. Вероятность взять первый билет, к которому студент не подготовился: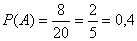 
. Вероятность взять второй из подготовленных билетов при условии, что студент взял первый билет, к которому он не подготовился: 
.
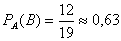В результате, вероятность того, что студенту достанется один из подготовленных билетов, вычисляется по формуле
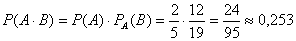
Выполнение теста.
Самостоятельная работа
Задача № 4.
Наиболее распространённая формулировка этой задачи, опубликованная в 1990 году в журнале ParadeMagazine, звучит следующим образом:
Представьте, что вы стали участником игры, в которой вам нужно выбрать одну из трёх дверей. За одной из дверей находится автомобиль, за двумя другими дверями — козы. Вы выбираете одну из дверей, например, номер 1, после этого ведущий, который знает, где находится автомобиль, а где — козы, открывает одну из оставшихся дверей, например, номер 3, за которой находится коза. После этого он спрашивает вас, не желаете ли вы изменить свой выбор и выбрать дверь номер 2. Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор?
Следует учесть,что участнику игры заранее известны следующие правила:
1.Автомобиль равновероятно размещён за любой из 3 дверей;
2.Ведущий в любом случае обязан открыть дверь с козой (но не ту, которую выбрал игрок) и предложить игроку изменить выбор;
3.Если у ведущего есть выбор, какую из 2 дверей открыть, он выбирает любую из них с одинаковой вероятностью.
Вариант.
Тема исследовательской работы «Выбор инновационной стратегии фирмы на основе оценки гипотез по Байесу»
|
|
|
Ход работы
Справка
|
|
|
