Согласно уравнению неразрывности для несжимаемой жидкости (29.1), объем, занимаемый жидкостью, остается постоянным, т. с.

Разделив выражение (30.5) на получим

где — плотность жидкости. Но так как сечения выбирались произвольно, то можем записать

(30.6)

Выражение (30.6) выведено швейцарским физиком Д. Бернулли (1700—1782; опуб­ликовано в 1738 г.) и называется уравнением Бернулли. Как видно из его вывода, уравнение Бернулли — выражение закона сохранения энергии применительно к устано­вившемуся течению идеальной жидкости. Оно хорошо выполняется и для реальных жидкостей, внутреннее трение которых не очень велико.

Величина в формуле (30.6) называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела), величина — динамическим давлением. Как

уже указывалось выше (см. § 28), величина представляет собой гидростатическое давление.

Для горизонтальной трубки тока выражение (30.6) принимает вид

(30.7)

где называется полным давлением.

Из уравнения Бернулли (30.7) для горизонтальной трубки тока и уравнения нераз­рывности (29.1) следует, что при течении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давле­ние больше в более широких местах, т. е. там, где скорость меньше. Это можно продемонстрировать, установив вдоль трубы ряд манометров (рис. 48). В соответствии с уравнением Бернулли опыт показывает, что в манометрической трубке В, прикреп­ленной к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С, прикрепленных к широкой части трубы.

Так как динамическое давление связано со скоростью движения жидкости (газа), то уравнение Бернулли позволяет измерять скорость потока жидкости. Для этого приме­няется трубка Пито — Прандтля (рис. 49). Прибор состоит из двух изогнутых под прямым углом трубок, противоположные концы которых присоединены к манометру. С помощью одной из трубок измеряется полное давление с помощью дру-

гой — статическое . Манометром измеряют разность давлений:

(30.8)

 

где 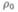— плотность жидкости в манометре. С другой стороны, согласно уравнению Бернулли, разность полного и статического давлений равна динамическому давле­нию:

(30.9) Из формул (30.8) и (30.9) получаем искомую скорость потока жидкости:

Уменьшение статического давления в точках, где скорость потока больше, положено в основу работы водоструйного насоса (рис. 50). Струя воды подается в трубку, открытую в атмосферу, так что давление на выходе из трубки равно атмосферному. В трубке имеется сужение, по которому вода течет с большей скоростью. В этом месте давление меньше атмосферного. Это давление устанавлива­ется и в откачанном сосуде, который связан с трубкой через разрыв, имеющийся в ее узкой части. Воздух увлекается вытекающей с большой скоростью водой из узкого конца. Таким образом можно откачивать воздух из сосуда до давления 100 мм рт. ст. (1 мм рт. ст.=133,32 Па).

Уравнение Бернулли используется для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жид­костью, в боковой стенке которого на некоторой глубине ниже уровня жидкости имеется маленькое отверстие (рис. 51).

Рассмотрим два сечения (на уровне свободной поверхности жидкости в сосуде и на уровне выхода ее из отверстия) и напишем уравнение Бернулли:

Так как давления в жидкости на уровнях первого и второго сечений равны

атмосферному, т. е. то уравнение будет иметь вид

Из уравнения неразрывности (29.1) следует, что где — площади

поперечных сечений сосуда и отверстия. Если то членом можно

Пренебречь и

 

Это выражение получило название формулы Торрачелли*.

Вязкость (внутреннее трение). Ламинарный и турбулентный режимы течения жидкостей

Вязкость (внутреннее трение) — это свойство реальных жидкостей оказывать сопротив- I ление перемещению одной части жидкости относительно другой. При перемещении одних слоев реальной жидкости относительно других возникают силы внутреннего трения, направленные по касательной к поверхности слоев. Действие этих сил проявля- ется в том, что со стороны слоя, движущегося быстрее, на слой, движущийся медлен- нее, действует ускоряющая сила. Со стороны же слоя, движущегося медленнее, на слой, движущийся быстрее, действует тормозящая сила.

Сила внутреннего трения F тем больше, чем больше рассматриваемая площадь I поверхности слоя 5 (рис. 52), и зависит от того, насколько быстро меняется скорость I течения жидкости при переходе от слоя к слою. На рисунке представлены два слоя, I отстоящие друг от друга на расстоянии и движущиеся со скоростями При I

этом Направление, в котором отсчитывается расстояние между слоями, I

перпендикулярно скорости течения слоев. Величина показывает, как быстро меняется I

скорость при переходе от слоя к слою в направлении х, перпендикулярном направле- I нию движения слоев, и называется градиентом скорости. Таким образом, модуль силы I внутреннего трения

(31.1)

где коэффициент пропорциональности зависящий от природы жидкости, называется динамической вязкостью (или просто вязкостью).

Единица вязкости — паскаль-секунда (Па - с): 1 Па с равен динамической вязкости среды, в которой при ламинарном течении и градиенте скорости с модулем, равным 1 м/с на 1 м, возникает сила внутреннего трения 1 Н на 1 м² поверхности касания слоев (1 Па. с= 1 Н • с/м²).

⇐ Предыдущая11121314151617181920Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: