 |
Силы и потенциальная энергия межмолекулярного взаимодействия
|
|
|
|
Модель идеального газа, используемая в молекулярно-кинетической теории газов, позволяет описывать поведение разреженных реальных газов при достаточно высоких температурах и низких давлениях. При выводе уравнения состояния идеального газа размерами молекул и их взаимодействием друг с другом пренебрегают. Повышение давления приводит к уменьшению среднего расстояния между молекулами, поэтому необходимо учитывать объем молекул и взаимодействие между ними. Так, в 1 м3 газа при нормальных условиях содержится 2,68.1025 молекул, занимающих объем примерно 10 -4 м3 (радиус молекулы примерно 10 -10 м), которым по сравнению с объемом газа (1 м3) можно пренебречь. При давлении 500 МПа (1 атм= 101,3 кПа) объем молекул составит уже половину всего объема газа. Таким образом, при высоких давлениях и низких температурах указанная модель идеального газа непригодна.
При рассмотрении реальных газов — газов, свойства которых зависят от взаимодействия молекул, надо учитывать силы межмолекулярного взаимодействия. Они проявляются на расстояниях < 10 -9 м и быстро убывают при увеличении расстояния между молекулами. Такие силы называются короткодействующими.
В XX в., по мере развития представлений о строении атома и квантовой механики, было выяснено, что между молекулами вещества одновременно действуют силы пратя-жеииа и силы отталкивания. На рис. 88, а приведена качественная зависимость сил межмолекулярного взаимодействия от расстояния г между молекулами, где Fo и Fa — соответственно силы отталкивания и притяжения, a F — их результиру-
|
|
ющая. Силы отталжнвания считаются положительными, а силы взаимного притяжения — отрицательными.
|
|
|
На расстоянии 
результирующая сила F=0, т. е. силы притяжения и оттал-
кивания уравновешивают друг друга. Таким образом, расстояние 
соответствует равновесному расстоянию между молекулами, на котором бы они находились в отсутствие теплового движения. При 
преобладают силы отталкивания (F>0), при 
— силы притяжения (F<0). На расстояниях 
м межмолекулярные силы взаимодействия практически отсутствуют 
Элементарная работа 
силы F при увеличении расстояния между молекулами на dr совершается за счет уменьшения взаимной потенциальной энергии молекул, т. е.
(60.1)
Из анализа качественной зависимости потенциальной энергии взаимодействия молекул от расстояния между ними (рис. 88, 6) следует, что если молекулы находятся друг от друга на расстоянии, на котором межмолекулярные силы взаимодействия не действуют 
то П=0. При постепенном сближении молекул между ними появляются силы притяжения 
которые совершают положительную работу 
Тогда, согласно (60.1), потенциальная энергия взаимодействия уменьшается, достигая минимума при 
При 
с уменьшением г силы отталкивания (F>0) резко возрастают и совершаемая против них работа отрицательна 
Потенциальная энергия начинает тоже резко возрастать и становится положительной. Из данной потенциальной кривой следует, что система из двух взаимодействующих молекул в состоянии устойчивого равновесия 
обладает минимальной потенциальной энергией.
Критерием различных агрегатных состояний вещества является соотношение между величинами 
— наименьшая потенциальная энергия взаимодействия молекул — определяет работу, которую нужно совершить против сил притяжения для того, чтобы разъединить молекулы, находящиеся в равновесии 
определяет удвоенную среднюю энергию, приходящуюся на одну степень свободы хаотического (теплового) движения молекул.
Если 
го вещество находится в газообразном состоянии, так как интенсив-
|
|
|
ное тепловое движение молекул препятствует соединению молекул, сблизившихся до расстояния 
т. е. вероятность образования агрегатов из молекул достаточно мала. Если 
то вещество находится в твердом состоянии, так как молекулы,
притягиваясь друг к другу, не могут удалиться на значительные расстояния и колеблются около положений равновесия, определяемого расстоянием 
Если 
то вещество находится в жидком состоянии, так как в результате теплового движения молекулы перемещаются в пространстве, обмениваясь местами, но не расходясь на расстояние, превышающее r0 .
Таким образом, любое вещество в зависимости от температуры может находиться в газообразном, жидком или твердом агрегатном состоянии, причем температура перехода из одного агрегатного состояния в другое зависит от значения 
для
данного вещества. Например, у инертных газов 
мало, а у металлов велико,
поэтому при обычных (комнатных) температурах они находятся соответственно в газообразном и твердом состояниях.
Уравнение Ван-дер-Ваальса
Как уже указывалось в § 60, для реальных газов необходимо учитывать размеры молекул и их взаимодействие друг с другом, поэтому модель идеального газа и уравне-
нне Клапейрона — Менделеева (42.4) pVm=RT (для моля газа), описывающее идеальный газ, для реальных газов непригодны.
Учитывая собственный объем молекул и силы межмолекулярного взаимодействия, голландский физик И. Ван-дер-Ваальс (1837—1923) вывел уравнение состояния реального газа. Ван-дер-Ваальсом в уравнение Клапейрона — Менделеева введены две поправки.
1. Учет собстииии объема молекул. Наличие сил отталкивания, которые проти
водействуют проникновению в занятый молекулой объем других молекул, сводится
к тому, что фактический свободный объем, в котором могут двигаться молекулы
реального газа, будет не Vm, a Vm—b, где b — объем, занимаемый самими молекулами.
Объем bравен учетверенному собственному объему молекул. Если, например, в сосуде находятся две молекулы, то центр любой из них не может приблизиться к центру другой молекулы на расстояние, меньшее диаметра d молекулы. Это означает, что для центров обеих молекул оказывается недоступным сферический объем радиуса d, т. е. объем, равный восьми объемам молекулы или учетверенному объему молекулы в расчете на одну молекулу.
|
|
|
2. Учет притяжения молекул. Действие сил притяжения газа приводит к появлению
дополнительного давления на газ, называемого внутренним давлением.По вычислени
ям Ван-дер-Ваальса, внутреннее давление обратно пропорционально квадрату моляр
ного объема, т. е.
(61.1)
где а — постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного притяжения, Vm — молярный объем.
Вводя эти поправки, получим уравнение Ван-дер-Ваальса для моля газа (уравнение состояния реальных газов):
(61.2)
Для произвольного количества вещества 
с учетом того, что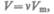 
|
|
|
