Давление под искривленной поверхностью жидкости

Если поверхность жидкости не плоская, а искривленная, то она оказывает на жидкость избыточное (добавочное) давление. Это давление, обусловленное силами поверхност­ного натяжения, для выпуклой поверхности положительно, а для вогнутой поверх­ности — отрицательно.

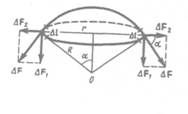
Для расчета избыточного давления предположим, что свободная поверхность жидкости имеет форму сферы радиуса R, от которой мысленно отсечен шаровой сегмент, опирающийся на окружность радиуса (ряс. 100). На каждый бес-

конечно малый элемент длины этого контура действует сала поверхностного натяжения касательная к поверхности сферы. Разложив на два компонента

видим, что геометрическая сумма сил равна нулю, так как эти силы на противоположных сторонах контура направлены в обратные стороны и взаимно уравновешиваются. Поэтому равнодействующая сил поверхностного натяжения, дей­ствующих на вырезанный сегмент, направлена перпендикулярно плоскости сечения внутрь жидкости и равна алгебраической сумме составляющих AF₁:

Разделив эту силу на площадь основания сегмента пг², вычислим избыточное давление на жидкость, создаваемое силами поверхностного натяжения и обусловленное кривиз­ной поверхности:

(68.1)

Если поверхность жидкости вогнутая, то можно доказать, что результирующая сила поверхностного натяжения направлена из жидкости и равна

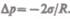(682)

Следовательно, давление внутри жидкости под вогнутой поверхностью меньше, чем в газе, на величину

Формулы (68.1) и (68.2) являются частным случаем формулы Лапласа*, опре­деляющей избыточное давление для произвольной поверхности жидкости двоякой кривизны:

(68.3) где — радиусы кривизны двух любых взаимно перпендикулярных нормальных

*П. Лаплас (1749—1827) — французский ученый.

 

Сечений поверхности жидкости в данной точке. Радиус кривизны положителен, если центр кривизны соответствующего сечения находится внутри жидкости, и отрицателен, если центр кривизны находится вне жидкости.

Для сферической искривленной поверхности выражение (68.3) перехо-

дит в (68.1), для цилиндрической 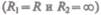- избыточное давление

В случае плоской поверхности силы поверхностного натяжения избыточ-

Юго давления не создают.

Капиллярные явления

Если поместить узкую трубку (капилляр) одним концом в жидкость, налитую в широ-сий сосуд, то вследствие смачивания или несмачивания жидкостью стенок капилляра кривизна поверхности жидкости в капилляре становится значительной. Если жидкость смачивает материал трубки, то внутри ее поверхность жидкости — мениск — имеет вогнутую форму, если не смачивает — выпуклую (рис. 101).

Под вогнутой поверхностью жидкости появится отрицательное избыточное давле­ние, определяемое по формуле (68.2). Наличие этого давления приводит к тому, что жидкость в капилляре поднимается, так как под плоской поверхностью жидкости в широком сосуде избыточного давления нет. Если же жидкость не смачивает стенки капилляра, то положительное избыточное давление приведет к опусканию жидкости в капилляре. Явление изменения высоты уровня жидкости в капиллярах называется капиллярностью. Жидкость в капилляре поднимается или опускается на такую высоту А, при которой давление столба жидкости (гидростатическое давление) уравновеши­вается избыточным давлением

где — плотность жидкости, — ускорение свободного падения.

Если - радиус капилляра, — краевой угол, то из рис. 101 следует, что откуда

(69.1)

В соответствии с тем, что смачивающая жидкость по капилляру поднимается, а несмачивающая — опускается, из формулы (69.1) при (cos0>O) получим

положительные значения Л, а при (cos0<O) — отрицательные. Из выражения

(69.1) видно также, что высота поднятия (опускания) жидкости в капилляре обратно пропорциональна его радиусу. В тонких капиллярах жидкость поднимается достаточно высоко. Так, при полном смачивании (0=0) вода (р=1000 кг/м^э, а= 0,073 Н/м) в ка­пилляре диаметром 10 мкм поднимается на высоту h=З м.

⇐ Предыдущая30313233343536373839Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: