 |
Правила округления при вычислениях
|
|
|
|
Результаты лабораторных измерений, а также справочные данные, используемые при обработке эксперимента, являются приближенным величинами. Приближенные величины, полученные в результате измерений, записываются приближенными числами.
При записи результатов измерений следует обязательно указывать величину абсолютной погрешности, или доверительный интервал, в который попадает истинное значение измеряемой величины с заданной доверительной вероятностью. Например,


Здесь же приводят и относительную погрешность
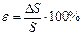
Полученный результат необходимо выделить - подчеркнуть или взять в рамку. Абсолютную погрешность выражают всегда в тех же единицах, что и измеряемую величину, например:
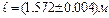

Общепринято и законодательно закреплено ГОСТ 8.011-72 правило, согласно которому абсолютная погрешность измерения определяется числом с количеством значащих цифр не более двух (значащими цифрами в числах принято называть все цифры 1,2,3,...,9, а также нуль, но только в тех случаях, если он стоит в середине или в конце, но не в начале).
Точность определения погрешности при элементарных методах обработки, которые излагаются студентам I курса, не превышает 30%. Это означает, что вторая значащая цифра абсолютной погрешности неверна и, следовательно, указывать погрешность с большей точностью не имеет смысла. Поэтому значение абсолютной погрешности следует округлять, оставляя одну значащую цифру. Только, если эта цифра равна единице, точность указания абсолютной погрешности одной цифрой окажется недостаточной (разница между 1 и 2 составляет уже 100%). В этом случае следует привести и вторую цифру, округлив её до 0 или до 5.
Другие двузначные числа, например, 2,5; 2,7; 3,5; и т.п. в записи погрешности не допускаются, так как такая запись претендует на неоправданную точность (при использовании более строгих методов обработки иногда удерживают и вторую цифру).
|
|
|
Напомним правило округления: округляя точное или приближенное число до определенного разряда, последнюю оставляемую значащую цифру не изменяют, если первая из отбрасываемых цифр меньше 5, и увеличивают на 1, если первая отбрасываемая цифра больше 5.
Если первая из отбрасываемых цифр равна 5, то последнюю из оставленных цифр сохраняют неизменной, если она четная и справа от неё стоит только цифра 5, последнюю из оставленных цифр увеличивают на единицу, если она нечетная и за ней стоит цифра 5. Как видно, этот случай не имеет обоснования и оправдывается лишь удобствами вычислительной практики. Например: требуется округлить числа 53,65 и 20,35 до первого знака после запятой. В результате получим: 53.6, 20.4.
Погрешность округления во всех случаях не превышает половины единицы разряда оставленной цифры.
В результате измерений или вычислений получают приближенное число, в котором различают цифры верные, не содержащие ошибок, и сомнительные, в которых содержатся ошибки. Принято приближенное число округлять и записывать в виде десятичной дроби, в которой все цифры, кроме последней, верные. Последней цифрой приближенного числа является сомнительная цифра. За её точность нельзя поручиться. Понятно, что порядок первой сомнительной цифры в приближенном числе определяется порядком первой значащей цифры абсолютной погрешности.
При записи относительной погрешности сохраняют не меньше двух Значащих цифр.
Приближенные величины такие, как π, e, √2, логарифмы чисел и т.п., приводимые в специальных таблицах, могут быть взяты, практически, с достаточной точностью. При вычислениях берут такие их значения, которые превышают на порядок точность других величин, входящих в данный расчет.
|
|
|
При использовании в расчетах табличных значений, для которых не указана погрешность, максимальную погрешность принимают равной 5 единицам разряда, следующего за порядком последней оставляемой значащей цифры.
Например, для табличного.значения коэффициента поверхностного натяжения воды при 20°С, равного σ = 72,53 10-3 Н/м. Результат записывается в виде:
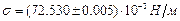
Погрешность, возникающую при округлении показаний приборов, называют погрешностью отсчитывания. Если показания прибора округляют к значению, соответствующему ближайшей отметке шкалы, то предел погрешности отсчитывания равен 0,5 цены деления шкалы прибора; если оценить на глаз десятую, пятую долю деления шкалы, то погрешность Отсчитывания не превышает 0,2 цены деления шкалы.
Чтобы получить результат косвенного измерения, выполняют математические операции, а затем округляют результат. Очевидно, нет необходимости выполнять математические операции с результатами прямых измерений, как с точными числами. Следует их округлять до определенного количества цифр. Это значительно облегчит работу, но при этом могут возникнуть дополнительные погрешности. Чтобы сам процесс вычисления не вносил дополнительной ошибки, все вычисления следует проводить с количеством значащих цифр, превышающих на единицу количество значащих цифр в самом неточном из исходных данных.
Так как значение абсолютной погрешности приводится с одной (реже с двумя) значащими цифрами, то все вычисления погрешностей следует производить не более, чем с двумя значащими цифрами. При этом может оказаться, что не все составляющие итоговой погрешности оказывают влияние на эту погрешность. Поэтому при вычислении итоговой погрешности некоторыми составляющими можно заранее пренебречь, если вклад их очень мал по сравнению с другими составляющими. Вышесказанное справедливо и в отношении итоговой относительной погрешности. Например: для измерения динамического коэффициента вязкости водного раствора глицерина по методу Стокса были выполнены измерения времени падения t стального шарика диаметра d и плотности с высоты h в цилиндрической трубе с водным раствором глицерина плотности ρ1.
|
|
|
Для расчета коэффициента вязкости используется формула
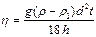
где g – ускорение свободного падения.
Были получены следующие результаты измерений с погрешностями после округления:
| t = (59,90 ± 0,15) c | 
|
| d = (1,010 ± 0,015) мм | 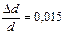
|
| h = (468,0 ± 0,5) мм | 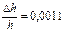
|
| ρ1 = (1,230 ± 0,007) г/см2 | 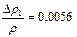
|
| ρ = (7,70 ± 0,5) г/см2 | 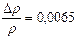
|
| g = (9,810 ± 0,005) м/с2 | 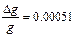
|
Относительная погрешность вязкости рассчитывается по формуле:

Из сравнения погрешностей результатов измерений видно, что наибольший вклад в погрешность косвенного измерения вносит погрешность измерения d. Тогда
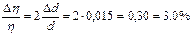
Строго говоря, отбрасывать все остальные погрешности можно, если выполняется неравенство


Проверяем:
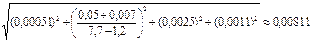
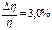
Следовательно,
Оформление графиков
При изучении зависимости одной величины от другой, результаты эксперимента могут быть представлены в виде графика.
Основное достоинство графиков – их наглядность. Построив график, экспериментатор сразу одним взглядом охватывает вид полученной зависимости, получает о ней качественное представление, отмечает наличие различных особенностей: максимумов, минимумов, точек перегиба, областей наибольшей и наименьшей скорости изменения, периодичности и т.п. График позволяет легко судить о соответствии экспериментальных данных той или иной теоретической зависимости, а также облегчает обработку измерений.
При построении графиков необходимо придерживаться следующих правил:
-графики должны выполнятся на миллиметровой бумаге или на бумаге со специальными координатными сетками;
-общепринято на оси абсцисс откладывать аргумент, т.е. ту величину, изменения которой являются причиной изменения другой, по оси ординат – функцию;
-масштабы по обеим осям выбирают независимо друг от друга. Однако, выбор масштаба для аргумента и функции должен быть сделан так, чтобы точность находимых графическим путем величин соответствовала точности измерений. Погрешность должна быть видна на графике и представляться отрезком достаточной длины, в противном случае график не отражает всех деталей эксперимента и не может быть использован для графической обработки данных без потери точности. При этом рекомендуется брать больший масштаб для той величины, погрешность измерений которой меньше.
|
|
|
Поясним это на примере. При измерении теплоты плавления записывают показания термометра Бекмана через каждую минуту в течение 20 минут. Цена деления термометра Бекмана равна 0,01 град. При достаточном навыке можно отсчитывать температуру с точностью до 0,002 град. Время измеряют по часам.
По результатам измерений на миллиметровой бумаге строят график. На оси абсцисс откладывают время, на оси ординат – температуру. Для оси времени достаточен масштаб 1 мин – 5 мм. Увеличение масштаба (например, до 1 мин – 1 см) будет бесполезным, только график станет более пологим. Для оси температур удобен масштаб 0,01 град – 2 мм. В этом случае точность отсчета температур по графику будет соответствовать точности измерений. Если выбрать меньший масштаб, например, 0,01 град – 1 мм, то отложить на графике величину 0,002 град, которую можно отсчитывать по термометру, не удастся. Больший масштаб, например, 0,01 град – 10 мм не нужен, так как ведя отсчет по графику, можно снять показания 0,5 мм = 0,0005 град, и ошибочно полагать, что такова точность полученного результата.
На графике приводится та область измерения измеренных величин, которая была исследована на опыте. Шкалы аргумента и функции должны начинаться с того значения, которое является ближайшим к наименьшему округленному, и кончаться ближайшим к наибольшему округленному значению данной величины. Так, если величина меняется в пределах от 0,53 до 0,97 единиц, то ось целесообразно слева ограничить 0,5, а справа 1,0. Не следует стремиться к тому, чтобы на графике обязательно поместилось начало координат (точка 0,0). Даже в том случае, когда требуется найти точку пересечения какой-либо прямой на графике с одной из координатных осей, нет необходимости, чтобы эта точка помещалась на графике. Точку пересечения легко найти расчетом, пользуясь подобием треугольников. Начало координат помещают на графике в том случае, когда это не требует большого увеличения его размеров и конечно тогда, когда (0,0) есть результат измерения (рис. 1).
При правильно выбранном масштабе построений угол наклона полученной кривой близок к 45º, а кривые занимают практически все поле чертежа. За единицы масштаба разумно выбирать числа, кратные 5, 10, 50, 100 мм, а также четные и нечетные числа. Не следует расставлять эти числа на осях графика слишком густо – достаточно нанести их через 2 или через 5 см. Не следует также проставлять экспериментальные точки. Около осей координат следует записать обозначение, единицы измерения, а иногда и название отложенных величин. Точки должны наноситься на график тщательно и аккуратно, чтобы график получился более точным. Это важно для дальнейшей графической обработки результатов. Если на координатной плоскости имеется несколько кривых, то каждой кривой присваивается номер, а на свободном поле чертежа указывается название, обозначение и единицы измерения параметра, соответствующего данному номеру. Точки, относящиеся к разным кривым, должны быть помечены различными символами (кружки, треугольники, квадраты и т.п.), чтобы не путать их.
|
|
|
Выносные линии на чертеже, как правило, не проводятся. Выносную линию можно нанести в виде исключения только в том случае, если хотят особо выделить на графике какую-либо точку (например, положение максимума).
Погрешность измерения изображают на графике с помощью отрезков, на середине которых находится экспериментальная точка. Длина отрезка равна удвоенной величине ошибки в данном масштабе. Отрезок сверху и снизу ограничивают черточками. Ошибку аргумента изображают горизонтальным отрезком, а ошибку функции – вертикальным.
В большинстве случаев можно заранее обеспечить желаемую точность аргумента. Кроме того, ошибка аргумента мала по сравнению с ошибкой в значении функции, поскольку в ошибку функции входят помимо ошибки аргумента еще и ошибки других величин. В таком случае на графике достаточно показать только ошибку функции с помощью вертикального отрезка (см. рис.2).
Кривую на графике проводят плавно, избегая изгибов и изломов. Кривая должна проходить насколько возможно ближе ко всем нанесенным точкам, но ни в коем случае не следует проводить её через каждую точку; экспериментальные точки должны располагаться по обе стороны от кривой.
Если на графике нанесены величины ошибок в виде вертикальных отрезков, то кривая, как правило, должна лежать в пределах этих отрезков.
Излом на кривой можно рисовать только в том случае, если его нельзя объяснить погрешностью измерений и если на его существование указывает большое число точек и отсутствие систематических ошибок. Следует помнить, что всякая особенность на кривой - излом, резкое изменение кривизны и пр. – требует либо специального экспериментального доказательства, либо теоретического объяснения.
Кривую на графике следует проводить от руки, карандашом. Готовый график снабжается заголовком, который должен содержать точное писание того, что показывает график.
Нахождение параметров теоретической или экспериментальной зависимости
Часто перед экспериментатором возникает задача: установить на основе опытных данных функциональную зависимость между измеряемыми физическими величинами. Например, представить найденную из опыта зависимость в виде полинома y = a + bx + cx2, показательной функции y = aebx и т.п. Вид уравнения можно подобрать произвольно или получить на основании каких-либо теоретических соображений. В обоих случаях необходимо проверить, пригодна ли данная формула для представления совокупности экспериментальных данных и подобрать как можно лучше значения неизвестных параметров a,b,c…, входящих в формулу. Для простых формул, содержащих один или два неизвестных параметра, удобно пользоваться графическим методом. Особенно просто решается задача для линейной функции y = a + bx, так как в этом случае график – прямая линия. Значение b находится как угловой коэффициент прямой («тангенс угла наклона» прямой к оси абсцисс), а значение a – как величина отрезка, отсекаемого прямой на оси ординат.
Если функция y = f(x) нелинейная, то в этом случае удобно использовать функциональный масштаб, т.е. график перечерчивается в новых координатах, выбранных так, чтобы получить линейную зависимость.
Так зависимость вида y = axn можно исследовать на графике 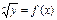 , если n известно. Если же n, как и a, неизвестные величины и их следует определить из экспериментальных данных, то применяется логарифмический масштаб lg y = f(lg x). В этом случае подбираемая функция представляется на графике прямой lg y = lg a + nlg x; параметры функции легко определяются из наклона и начальной ординаты прямой. Функция вида y = a + bx2 подбирается на графике y = f(x2), т.е. по оси абсцисс откладывают значения x2. Экспоненциальная функция вида y = ax2e-b/x изобразится прямой в координатах lg y/x2 и 1/x (
, если n известно. Если же n, как и a, неизвестные величины и их следует определить из экспериментальных данных, то применяется логарифмический масштаб lg y = f(lg x). В этом случае подбираемая функция представляется на графике прямой lg y = lg a + nlg x; параметры функции легко определяются из наклона и начальной ординаты прямой. Функция вида y = a + bx2 подбирается на графике y = f(x2), т.е. по оси абсцисс откладывают значения x2. Экспоненциальная функция вида y = ax2e-b/x изобразится прямой в координатах lg y/x2 и 1/x (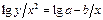 ).
).
Обычно при таком методе обработки результатов измерений строят два графика – график в функциональном масштабе для количественной обработки и график в натуральном масштабе для наглядного представления функции.
Метод наименьших квадратов
При эмпирическом (экспериментальном) изучении функциональной зависимости одной величины  от второй
от второй 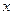 , проводят ряд измерений величины
, проводят ряд измерений величины 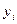 при разных значениях
при разных значениях 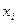 , т.е. получают набор
, т.е. получают набор 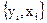 . Результаты могут быть представлены в виде таблицы или графика (рис.1).
. Результаты могут быть представлены в виде таблицы или графика (рис.1).

|
Задача заключается в аналитическом воспроизведении функциональной зависимости между этими величинами, т.е. в подборе функции  , которая описывает результаты измерений. Особенность задачи заключается в том, что наличие случайных погрешностей измерения (или, как говорят, наличие “шума” в эксперименте) делает неразумным подбор такой формулы, которая бы точно описывала экспериментальные значения. Другими словами, график воспроизводимой зависимости не должен проходить через все точки на рис. 1, а должен по возможности сглаживать “шум”. Конечно, сглаживание “шума” будет тем точнее, чем большее количество измерений.
, которая описывает результаты измерений. Особенность задачи заключается в том, что наличие случайных погрешностей измерения (или, как говорят, наличие “шума” в эксперименте) делает неразумным подбор такой формулы, которая бы точно описывала экспериментальные значения. Другими словами, график воспроизводимой зависимости не должен проходить через все точки на рис. 1, а должен по возможности сглаживать “шум”. Конечно, сглаживание “шума” будет тем точнее, чем большее количество измерений.
Эмпирические формулы обычно выбирают из зависимостей определенного типа (наиболее простых), например,
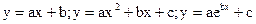 и т.д.
и т.д.
Другими словами, задача сводится к определению параметров 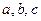 ... на основе полученных экспериментальных данных, в то время как вид зависимости выбрано заранее, из каких-либо теоретических соображений или интуитивно.
... на основе полученных экспериментальных данных, в то время как вид зависимости выбрано заранее, из каких-либо теоретических соображений или интуитивно.
Если все измерения величин 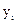 и
и 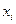 проведенные с одинаковой точностью, то параметры
проведенные с одинаковой точностью, то параметры  находятся из условия, что сумма квадратов отклонений экспериментальных значений
находятся из условия, что сумма квадратов отклонений экспериментальных значений 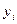 от рассчитанных
от рассчитанных  , т.е. величина
, т.е. величина
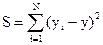 , (1)
, (1)
принимала наименьшее значение (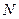 - число измерений).
- число измерений).
Поиск значений 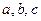 ..., которые приводят к наименьшему значению функции
..., которые приводят к наименьшему значению функции 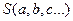 , сводится к решению системы уравнений:
, сводится к решению системы уравнений:
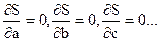 (2)
(2)
Рассмотрим решение этой задачи на примере линейной аппроксимации
 . (3)
. (3)
Тогда (3) принимает вид
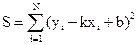 . (4)
. (4)
Применим условие (2) к (4):
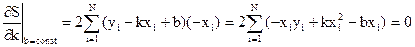 .
.
Откуда:
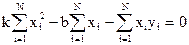 . (5)
. (5)
Аналогично:
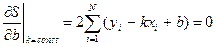 ,
,
т.е.
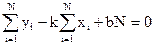 . (6)
. (6)
Уравнение (5) – (6) представляют собой систему уравнений с двумя неизвестными 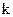 и
и 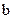 . Решив ее, получим:
. Решив ее, получим:
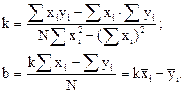 (7)
(7)
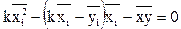
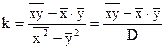 ,
,
где D – дисперсия.
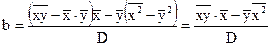 .
.
Лабораторная работа № 1
|
|
|


