Изучение броуновского движения. Определение постоянной Больцмана.

Цель работы: на примере непосредственного наблюдения броуновского движения проверить уравнение Эйнштейна, ознакомиться c методом наблюдения броуновского движения твердых частиц в жидкости.

Теоретический материал.

Броуновское движение. Теория Эйнштейна-Смолуховского. Определение числа Авогадро. Флуктуации и средние плотности в частях объема их зависимость от величины этих частей. Статистический характер второго начала термодинамики. Связь энтропии и термодинамической вероятности. Объективный характер статистической закономерности. Пример флуктуации макроскопических параметров. Границы применимости второго закона термодинамики.

 

Взвешенные в жидкости очень мелкие твердые частицы находятся в состоянии непрестанного беспорядочного движения, называемого броуновским движением. Причина его заключается в том, что при достаточно малых размерах частиц импульсы, сообщаемые частице ударяющимися о нее с разных сторон молекулами, оказываются некомпенсированными. О частицу заметных размеров ударяется одновременно большое число молекул, так что суммарный результат ударов достаточно хорошо усредняется. При малых размерах частицы начинают проявляться отклонения скоростей отдельных молекул и числа ударяющихся молекул от средних значений. Поскольку отклонения от средних значений (флуктуации) обычно бывают кратковременными, то через короткий промежуток времени направление равнодействующей силы изменится, а вместе с ней изменится и направление перемещения частицы. Следовательно, движение частицы будет хаотичным, беспорядочным, отражающим хаотичность молекулярного движения.

Долгое время броуновское движение являлось лишь качественным подтверждением молекулярно-кинетической теории.

Статистическое истолкование и установление количественных соотношений для броуновского движения было дано лишь в начале двадцатого столетия в работах Эйнштейна и, независимо от него, Смолуховского(1905г).

Ниже приводится более простой, чем у этих авторов, вывод основного соотношения этой теории.

Если скорость или число молекул, ударяющихся о частицу с одной стороны, окажется иной, чем для молекул, ударяющихся с другой стороны, то результирующий импульс, сообщаемый частице, будет отличен от нуля, и частица начнет двигаться в соответствующем направлении. В следующий момент времени результирующий импульс будет иметь иное направление. Следовательно, частица будет все время перемещаться беспорядочным образом.

Вследствие неполной компенсации импульсов от ударов молекул на броуновскую частицу действует некоторая результирующая сила F, под действием которой частица и движется. Кроме этой силы на частицу действует сила трения, вызванная вязкостью среды и направленная против силы F.

Если предположить, что частицы имеют форму сферы, то есть, что сила f определяется формулой Стокса f= 6 , то уравнение движения частицы запишется в виде:

m = (1)

Здесь m – масса частицы, - ее радиус, - радиус-вектор относительно произвольной системы координат, - скорость частицы.

Рассмотрим проекцию радиус-вектора на одну из координатных осей, например на ось х. Для этой составляющей уравнение движения перепишется в виде:

(2)

Найдем смещение х броуновской частицы, которое она получит под действием ударов молекулы. Поскольку смещения с равной вероятностью могут иметь и положительный, и отрицательный знак, то среднее смещение . Но не будет равным нулю среднее значение квадрата смещения . Преобразуем поэтому уравнение (2) так, чтобы в него входила величина . Для этого обе части уравнения умножим на х

(3)

Используем очевидные тождества

и

Подставив эти выражения в (3), получим:

(4)

Это равенство справедливо для любой частицы и поэтому оно справедливо также и для средних значений, входящих в него величин, если усреднение вести по достаточно большому числу частиц. Поэтому можно написать

где - среднее значение квадрата перемещения частицы вдоль оси х;

- среднее значение квадрата ее скорости по оси х;

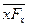=0, так как для большого числа частиц 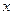и одинаково часто принимают как положительные, так и отрицательные значения.

Из хаотичности движения следует, что средние значения квадратов составляющих скоростей по всем трем координатным осям равны друг другу. Из того, что

следует, что

(5)

Можно записать, что средняя кинетическая энергия броуновской частицы . Достаточно малые частицы вовлекаются в совершаемое молекулами тепловое движение. Обмениваясь энергией с молекулами жидкости, они находятся в тепловом равновесии со средой, в которой они движутся, то есть средняя кинетическая энергия броуновской частицы равна средней кинетической энергии молекул жидкости и, следовательно,

(6)

То, что средняя кинетическая энергия броуновской частицы равна имеет принципиальное значение. Выражение для энергии одинаково независимо от того рассматриваются ли отдельные молекулы или броуновские частицы, содержащие миллиарды молекул.

Броуновскую частицу можно рассматривать как гигантскую молекулу.

Вернемся к уравнению движения, которое с учетом (6) запишем в виде

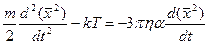
Это уравнение легко интегрируется. Обозначив , получаем и после разделения переменных

Интегрируя левую часть этого уравнения в пределах от 0 до z, и правую от 0 до t, получаем

или

отсюда

Величина в обычных условиях опыта ничтожно мала. Действительно, размеры броуновских частиц не превышают см, вязкость воды приблизительно пуаз, плотность вещества порядка единицы, следовательно масса броуновской частицы г.

Показатель степени при таков, что величиной можно пренебречь.

Следовательно, если отрезок времени между последовательными наблюдениями за частицей превышают с, что всегда имеет место, то

(7)

Для конечных промежутков времени и соответствующих перемещениях можно записать

и (8)

то есть среднее значение квадрата перемещения броуновской частицы за промежуток времени вдоль оси х, или любой другой оси, пропорционально этому промежутку времени. Формула (8) дает возможность определить постоянную Больцмана и число Авогадро. Одной из задач работы является проверка соотношения (8), которое носит название закона Эйнштейна-Смолуховского.

Экспериментальная установка.

Броуновское движение хорошо наблюдать на почти сферических частицах гуммигута, взвешенных в воде. Размер таких частиц очень мал (порядка 10^-5 см) и поэтому их удобнее наблюдать в рассеянном свете. Для этого свет от источника направляют в препарат с помощью конденсора темного поля. На рисунке 1 показан ход лучей в параболоиде конденсора. Параллельный пучок лучей падает на плоско-выпуклое стеклянное тело Р, боковая поверхность которого является параболоидом вращения. Центральные лучи малой апертуры задерживаются заслонкой В, а боковые лучи с большей апертурой отражаются от боковой поверхности параболоида, проходят через иммерсионный слой F, предметное стекло, препарат и покровное стекло. На верхней поверхности последнего лучи претерпевают полное внутреннее отражение, благодаря чему выходят наружу через ту же нижнюю грань конденсора, через которую вошли.

Рис. 2

Если на своем пути в препарате лучи встретят частицу, размеры которой соизмеримы с длиной волны, то они рассеиваются на ней, благодаря чему часть их энергии попадает в микроскоп и образует в нем дифракционное изображение в виде светящейся точки или системы светлых колец. Форма этого изображения, вообще говоря, не будет отображать в точности форму самой частицы. Однако, если отказаться от желания получить хотя бы приблизительно сходное изображение предмета и стремиться только обнаружить его существование и положение, то описанный прием позволит установить наличие частиц и их положение.

Для зарисовки пути частиц в данной работе используется рисовальный аппарат, который укрепляется на тубусе микроскопа. Схема его дана на рис.2. Над окуляром микроскопа помещен стеклянный кубик abcd, диагональное сечение которого ac посеребрено со стороны, обращенной к глазу. В центре сечения оставлен непосеребренный зрачок. Через него лучи из микроскопа попадают в глаз. Параллельно с ним в глаз попадает изображение листа бумаги А после отражения от зеркала В и посеребренного сечения ac. Зрачок кубика значительно суживает поле зрения микроскопа. Этот недостаток частично устраняется тем, что кубик может перемещаться над окуляром с помощью специальных винтов. Изменение яркости изображения бумаги производится поворотом колпака кубика, имеющего На боковой поверхности шесть окошек, пять из которых снабжены дымчатыми стеклами различной степени затемнения. Яркость изображения объекта регулируется с помощью фильтров, вставленных в шайбу, которая располагается между кубиком и тубусом микроскопа. Кубик с затемняющими приспособлениями может быть отведен в сторону. В работе проверяется выполнение закона Эйнштейна-Смолуховского (8).

 

Порядок выполнения работы.

 

В луночку предметного стекла пипеткой наносят 3-4 капли суспензии гуммигута. Препарат накрывают сверху чистым покровным стеклом. При этом нужно следить, чтобы под покровным стеклом не оставались пузырьки воздуха. Избыток жидкости, выступающий из-под стекла, удаляют фильтровальной бумагой. Свет осветителя с помощью зеркала направляется так, чтобы поле зрения было центрировано и освещено равномерно и наиболее интенсивно. После этого на верхнюю линзу конденсора наносится капля иммерсионной жидкости. На предметном столике закрепляют препарат. Конденсор поднимается вверх до тех пор, пока капля иммерсионной жидкости не коснется предметного стекла и расползется в тонкий слой. Необходимо следить за тем, чтобы предметное стекло лежало на столике, а не на конденсоре, так как последний легко повредить.

Фокусировку микроскопа производят при отведенном кубике рисовального аппарата. При этом следует соблюдать осторожность, чтобы не раздавить покровное стекло. Под зеркало рисовального аппарата на столике помещают лист бумаги и добиваются того, чтобы через рисовальный аппарат были хорошо видны одновременно частицы гуммигута и острие карандаша на бумаге. Выбрав хорошо заметную движущуюся частицу, совмещают кончик карандаша с ее изображением и включают секундомер. Все время следя глазом за частицей, соединяют карандашом положение частицы в момент включения секундомера с ее положениями через 5 секунд, через 10 секунд и т.д. Так как требуется установить статистическую закономерность, то результат получается тем точнее, чем больше будет снято точек. Опыт следует повторить для 2-3 частиц. После окончания каждого опыта следует точки пронумеровать.

 

Обработка результатов измерений.

В опытах необходимо получить не менее 20 последовательных положений броуновской частицы через каждые 5 секунд. Однако необходимо учитывать, что полученное изображение получается увеличенным.

Для проверки закона Эйнштейна-Смолуховского необходимо определить средние квадраты перемещения частицы за 5, 10 и 15 секунд, то есть средний квадрат расстояний между двумя последовательными положениями изображений частицы через соответствующие промежутки времени. Затем строят график, на оси абсцисс которого откладывают промежутки времени n (n=1,2,3; =5 c), а на оси ординат значения для соответствующих промежутков времени в удобном масштабе. Если нанесенные таким образом точки можно соединить прямой линией, проходящей через начало координат, то эксперимент полностью подтверждает теорию (см. формулу 8).

Для определения последовательных перемещений броуновской частицы поступают следующим образом: сначала концы раздвижного циркуля-измерителя совмещают с отмеченными на бумаге нужными точками, а затем циркуль-измеритель переносится на миллиметровую линейку, по которой и определяется перемещение с точностью 0,5 мм. Результаты подобных измерений перемещений частицы заносятся в таблицу.

 

t = 5с	t = 10с	t = 15с
Сполучення точок			Сполучення точок			Сполучення точок
1–2			1–3			1–4
2–3			2–4			2–5

 

Затем вычисляются , и

И окончательно , , .

Контрольные вопросы:

1. Какое движение называют броуновским? Приведите примеры броуновского движения? В чем причина такого характера движения?

2. Что такое флуктуации? От чего зависит величина флуктуации? Флуктуацией какого параметра системы вызвано движение броуновской частицы?

3. Почему теория броуновского движения, разработанная Эйнштейном-Смолуховским, позволила использовать это явление для подтверждения молекулярно-кинетической теории? Дайте вывод уравнения Эйнштейна.

4. Зависит ли броуновское движение от рода вещества частиц? от плотности вещества? от формы и размера частиц? от вязкости среды? от температуры?

5. Почему средняя сила, действующая со стороны молекул на покоящуюся частицу, равна нулю, а на движущуюся – не равна нулю? Почему эта сила, пропорциональна первой степени скорости и направлена против скорости?

6. Объясните, почему более мелкие броуновские частицы движутся быстрее, а более крупные медленнее. Означает ли это, что средний квадрат перемещения броуновской частицы зависит от ее массы и будет тем больше, чем меньше ее масса?

7. В чем заключается метод, позволяющий наблюдать столь мелкие частицы как броуновские? Можно ли путем прямых измерений определить размер броуновской частицы?

8. Объясните, почему в метрологии броуновское движение рассматривают как основной фактор, ограничивающий точность чувствительных измерительных приборов. Когда можно считать, что предел точности измерений достигнут?

9. Объясните, с помощью какого устройства можно наблюдать вращательное броуновское движение?

10. Во II начале термодинамики утверждается о невозможности вечного двигателя II рода и о возрастании энтропии в изолированной системе. Наблюдаемое броуновское движение частиц находится в противоречии с приведенными утверждениями, так как броуновская частица получает энергию от молекул окружающей среды, температура которой не выше, чем температура самой броуновской частицы. Объясните, какое из приведенных двух утверждений II начала остается в силе, а какое требует уточнения, т.е. имеет ограниченную область применения.

 

Литература:

1. Физический практикум под редакцией В.И. Ивероновой. Механика и молекулярная физика. -М., 1967.

2. А.Н. Матвеев. Молекулярная физика, -М.; Высшая школа, 1981, гл.1.

3. А.К. Кикоин, И.К. Кикоин. -М., 1976, гл. I, §7.

4. Д.В. Сивухин. Общий курс физики. Термодинамика и молекулярная физика, т. II, гл.V.

 

Лабораторная работа № 3

Определение коэффициента диффузии водяных паров в воздухе.

 

Цель работы: определить коэффициент диффузии паров воды в воздухе по испарению капли.

Теоретический материал: явления переноса, кинематические характеристики молекулярного движения, длина свободного пробега, экспериментальное определение поперечного сечения столкновений, диффузия, теплопроводность, вязкость идеального газа.

 

Основное уравнение явлений переноса.

Равновесное состояние газа в молекулярно-кинетической теории рассматривается как состояние полной хаотичности движения молекул, распределение которых по скоростям подчиняется закону Максвелла. Любое нарушение равновесия всегда связано с нарушением хаотичности движения и максвелловского распределения по скоростям. Основной особенностью неравновесных состояний является стремление газа самопроизвольно переходить к равновесному состоянию. Это обусловлено хаотическим тепловым движением молекул и непрерывными их столкновениями, которые приводят к постоянному перемешиванию молекул, изменению их скоростей и энергий.

Переход газа в равновесное состояние всегда связан с направленным переносом массы, импульса и энергии. Поэтому соответствующие процессы объединены под общим названием явлений переноса.

Каждое явление переноса бывает обусловлено неодинаковостью значений некоторой физической величины (концентрации, температуры) в разных точках пространства. Если в различных частях объёма газа, его плотность неодинакова, то с течением времени происходит выравнивание плотностей. Это явление называют диффузией. В этом случае переносимой физической величиной является масса. Из области газа с большей плотностью молекулы диффундируют в область с меньшей плотностью.

Если в разных частях объема различна температура, то происходит постепенное её выравнивание за счет переноса молекулами энергии. Соответствующее явление называется теплопроводностью.

Наконец, при ламинарном течении газа между отдельными его слоями в результате теплового хаотического движения молекул происходит перенос молекулами своего импульса. В результате, между слоями газа возникает внутреннее трение. Поскольку механизм перечисленных процессов одинаков, то и уравнение, описывающее эти процессы, будет общим.

Выведем общее уравнение переноса, не конкретизируя, какую именно величину переносят молекулы. Обозначим эту величину через φ, то есть φ – это может быть и масса, и импульс, и энергия молекулы. В случае равновесного состояния φ постоянна по объему газа. При наличии неоднородностей в газе, например, по концентрации или температуре, возникает градиент величины φ и имеет место поток этой величины в направлении его уменьшения.

Рис. 1

Выделим в газе площадку dS, перпендикулярную оси x, вдоль которой поддерживается, например, постоянная разность концентраций или температуры, или, в общем случае, градиент физической величины φ. Поскольку обмен значениями φ(х) происходит только при взаимодействии молекул, то есть на расстоянии порядка средней длины свободного пробега λ, то и значение φ(х) можно считать неизменным лишь на расстоянии λ слева и справа от площадки dS. Поскольку λ – величина достаточно малая, то φ(х) можно разложить в ряд по степеням этой величины и, ограничившись членом первой степени малости, записать:

В предположении, что тепловые скорости молекул не зависят от направления и их средние значения равны , можно записать, что поток молекул в направлении оси х равен , где n₀ – равновесная концентрация молекул.

Следовательно поток физической величины φ через площадку dS в направлении отрицательных значений х равен:

а в направлении положительных значений

Полный поток в положительном направлении оси х в любой точке будет равен:

(1)

Это уравнение является основным уравнением процессов переноса.

Если в некотором объеме газа имеется неоднородность плотности, то возникает диффузия. Переносимой физической величиной в этом случае является масса молекулы m. С учетом из уравнения (1), получаем уравнение стационарной диффузии или закон Фика:

(2)

Величину называют коэффициентом диффузии.

При фиксированной температуре , a , следовательно, Если постоянно давление, то , a . Значит . Соотношение , которое удобно записать в виде DP = Const, соблюдается в достаточно широком интервале давлений для не очень плотных газов с точностью до нескольких десятков процентов. В зависимости от температуры D растет несколько быстрее, чем Т^3/2.

Значения коэффициентов диффузии газов необходимо знать для расчета различных диффузионных процессов в физико-химической гидродинамике. Например, для расчета процессов горения жидких и твердых топлив, процессов смешения газов и т.п.

Расчет испарения капли в неподвижной среде. Изучение кинетики испарения капель различных жидкостей позволяет экспериментально определить коэффициенты диффузии паров.

Пусть сферическая капля воды с начальным радиусом R₀ находится в воздухе с относительной влажностью f при температуре Т. Скорость испарения капли определяется скоростью диффузии пара из приповерхностного слоя и количества тепла, поступающего к капле извне благодаря теплопроводности и расходуемого на ее исчерпание. Будем считать процесс испарения квазистационарным. На поверхности капли ее пар является насыщенным, температура капли постоянна. Тогда масса dm пара, диффундирующего через произвольную сферическую поверхность радиуса r, концентрическую с поверхностью капли, равна:

(3)

где ρ – плотность пара.

Так как процесс квазистационарный, то эта величина не будет зависеть от r. Это приводит к уравнению

, где

После интегрирования получим , где - плотность пара на бесконечном удалении от капли.

Величину А можно найти, приняв во внимание, что на поверхности капли пар насыщенный, то есть, что при r=R и, следовательно, ρ=ρ_нас,

А=R(ρ_{нас -} ρ_∞)

Тогда

С другой стороны радиус капли R меняется в процессе ее испарения и поэтому

(ρ_ж – плотность жидкости).

Сопоставляя эти два выражения для dm/dt, получим

Пренебрегая зависимостью ρ_нас от кривизны поверхности капли, то есть для достаточно крупных капель, найдем после интегрирования

или, если известна относительная влажность,

Таким образом, процесс испарение капли описывается линейным законом изменения ее площади поверхности с течением времени. Этот закон впервые установил Срезневский.

Комплекс называется константой скорости испарения.

Задачей теоретического анализа процесса испарения является выявление зависимости К от свойств жидкости, среды и условий испарения. Мы ограничимся экспериментальным определением константы скорости испарения в простейшем случае неподвижной среды для вычисления коэффициента диффузии водяного пара.

 

Методика проведения эксперимента.

В соответствии с линейным законом испарения капли квадрат ее диаметра

(4)

Таким образом, если экспериментально проследить за изменением диаметра испаряющейся капли во времени и построить график зависимости d²=f(t), то из графика легко получить значение константы скорости испарения по тангенсу угла наклона прямой d²(t) к оси абсцисс. Определив температуру среды и капли и измерив относительную влажность воздуха, можно рассчитать коэффициент диффузии водяного пара в воздухе

(5)

Определим из таблиц давление насыщенных паров при температуре Т, тогда, используя соотношения

выражение (5) можно записать в виде

μ - молярная масса воды, R – универсальная газовая постоянная, Т – температура капли.

Экспериментальная установка представляет собой камеру с прозрачными стенками, внутри которой на спае термопары с помощью пипетки подвешивается капля воды. С помощью микроскопа следят за уменьшением диаметра капли в процессе испарения.

 

Эксперимент выполняется в следующем порядке.

1. По термометру, находящемуся в камере, определяют температуру среды Т_∞

2. Относительную влажность воздуха в камере регистрируют по показаниям гигрометра.

3. С помощью пипетки на спай термопары подвешивают каплю воды.

4. По показаниям термопарного гальванометра определяют разность температур среды и капли (Т_∞ - Т).

5. С помощью микроскопа определяют начальный диаметр капли. Увеличение микроскопа определяют перед началом опыта.

6. Включают секундомер и через равные промежутки времени регистрируют диаметр испаряющейся капли. Данные заносят в таблицу. В опытах необходимо получить не менее 10 значений диаметра d для 5 различных капель.

 

T	0	t1	t2	t3	t4	t5
D	D0	d1	d2	d3	d4	d5

 

7. По результатам экспериментов строят зависимости d²=f(t) для каждой капли и определяют константу скорости испарения, используя закон Срезневского (4).

8. Формулы (5) и (6) позволяют рассчитать коэффицинты диффузии паров воды по скоростям испарения каждой капли.

9. По полученным для каждой капли коэффициентам диффузии определяют погрешность серии экспериментов в соответствии с теорией погрешностей.

10. В заключение необходимо рассчитать коэффициент диффузии паров воды по формуле и сравнить с экспериментально найденным.

Лабораторная работа №4

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: