 |
Внутреннее трение в жидкостях. Температурная зависимость коэффициента вязкости жидкости. Определение энергии активации
|
|
|
|
Цель работы: методом капиллярного вискозиметра определить зависимость коэффициента вязкости жидкости
a) от концентрации раствора,
b) от температуры;
оценить точность эксперимента.
Теоретический материал: Физическая сущность процессов переноса – диффузии, теплопроводности и внутреннего трения. Стационарные и нестационарные процессы и их уравнения. Элементарная теория явлений переноса. Выражение коэффициента вязкости через величины, характеризующие молекулярное движение. Характеристика жидкого состояния. Модели жидкости. Ближний и дальний порядок. Молекулярное взаимодействие и тепловое движение. Вязкость жидкости. Течение в тонких трубах, формула Пуазейля.
Основные представления.
Молекулы жидкости не связаны с неподвижными центрами колебаний, как в кристаллах, и движутся не так свободно, как в газах. Каждая молекула жидкости окружена со всех сторон тесным кольцом других молекул, которые отстоят от нее в среднем на расстоянии, равном ее диаметру. Если соседние молекулы разойдутся на достаточное расстояние или молекула при столкновении получит энергию, достаточную для того, чтобы раздвинуть соседние молекулы, то она перейдет на новое место. Здесь она будет совершать колебания до тех пор, пока снова не создадутся условия для ее перемещения на другое место.
Частота колебаний молекул жидкости в среднем равна 
Гц. Она не постоянна. Со временем изменяется энергия и амплитуда колебаний молекул. Поступательное движение молекул среди других таких же молекул называется самодиффузией. Минимальная энергия, необходимая для того, чтобы молекула жидкости(или твердого тела) могла переместиться из одного временного положения равновесия в другое, называется энергией активации самодиффузии. Величина этой энергии 
зависит от степени упорядоченности размещения молекул и от величины межмолекулярных сил. Так как упорядоченность в жидкости меньше и межмолекулярные силы слабее, чем в кристалле, то и энергия активации самодиффузии в жидкости меньше, чем в твердом состоянии. Это обуславливает более частые переходы с места на место в жидкостях. Ежесекундно молекула жидкости успевает переменить место около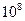 
раз, совершая между двумя последовательными переходами 
колебаний.
|
|
|
Ежесекундно число 
активированных скачков молекулы, очевидно, тем больше, чем больше частота колебаний 
, чем меньше энергия активации и чем выше температура 
. Зависимость частоты скачков молекулы от температуры можно выразить приближенной формулой
(1)
Здесь 
учитывает размещение ближайших соседей, так как для скачка молекулы нужна не только энергия активации, но еще и благоприятное расположение ближайших соседей. Такие скачки молекул объясняют значительное возрастание коэффициента диффузии в жидкости по сравнению с его значением в твердых телах. Типичный порядок коэффициента диффузии 
в жидкостях 
, а в твердых телах 
. В этом смысле жидкости ближе к газам, для которых D имеет порядок 
С этим же связано появление текучести жидкости - основного свойства, отличающего ее от твердого тела. Текучесть характеризуется величиной обратной вязкости: чем меньше вязкость, тем больше текучесть. Текучестью, естественно, обладают и газы, имеющие вязкость меньшую, чем жидкости.
Однако, механизмы подвижности молекул жидкостей и газов различны. Это видно при сопоставлении температурной зависимости вязкости веществ в обоих этих состояниях: вязкость газов растет с температурой, а вязкость жидкостей уменьшается. В газе молекулы большую часть времени находятся в свободном, прямолинейном и равномерном движении и только при столкновениях изменяют свою скорость. Поэтому можно считать, что вязкость газа обусловлена выравниванием скоростей молекул в разных слоях в результате взаимных столкновений. Для газов коэффициент вязкости 
, являющийся мерой этого выравнивания, пропорционален коэффициенту диффузии и поскольку 
, то и 
.
|
|
|
Механизм возникновения вязкости в жидкостях не удается представить столь просто, как в разреженных газах, когда картина сводится к переносу импульса упорядоченного движения газа при переходе из одного слоя в другой в результате молекулярного движения. Если принять эту картину и применить механизм скачков молекулы из оседлого положения в одном слое в оседлое положение молекулы в другом слое, то для динамической вязкости получается противоречащая эксперименту зависимость от температуры, а именно 
, в то время как эксперимент показывает зависимость вида 
.
Картина "скачков" молекулы из одного оседлого положения в другое может быть в определенных пределах сохранена. Молекулы жидкости участвуют, главным образом, в колебательном движении и только время от времени совершают скачки на расстояние, равное диаметру молекулы. Эти перескоки необходимо рассматривать в направлении, перпендикулярном градиенту скорости. При этом процесс оказывается зависимым от конкретных особенностей межмолекулярных сил. Молекуле приходится вырываться из своего окружения, чтобы передвинуться в направлении действия силы.
Если внешняя сила постоянна, то в направлении этой силы молекула будет совершать перемещение со скоростью
(2)
где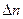 
- разность чисел ежесекундных скачков в направлении силы и в противоположном направлении, а 
- длина одного скачка.
Допустим, что один слой жидкости движется со скоростью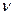 
относительно соседнего, находящегося на расстоянии от него. Тогда градиент скорости 
,
а величина сдвигового напряжения
(3)
На молекулу, площадь сечения которой 
, действует сила 
. Допустим, что эта сила действует на пути 
, пока молекула преодолевает потенциальный барьер, полуширина которого . Тогда работа совершаемая силой при перемещении молекулы
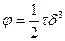(4)
Энергия активации уменьшается на величину этой работы при скачке молекулы в направлении силы и настолько же увеличивается при скачке в противоположном направлении. Поэтому, согласно (1) числа скачков молекулы в прямом и обратном направлениях определяются выражениями
|
|
|
Это обуславливает суммарный перенос молекул в направлении действия силы
(5)
Величина в скобках есть удвоенный гиперболический синус, то есть
Гиперболический синус можно представить в виде ряда
При 
то есть когда работа 
, совершаемая молекулой, гораздо меньше энергии теплового движения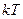 
молекулы можно приближенно положить, что
Тогда (5) преобразуется к виду
(6)
Или, если воспользоваться значением из (4)
(7)
Подставляя (7) в (3), находим (8)
(8)
Первый множитель в (8) при повышении температуры меняется гораздо медленнее, чем второй. Поэтому в не слишком большом интервале температур первый множитель в (8) можно считать постоянным, не зависящим от температуры. Тогда (8) можно записать в следующем виде
Эту формулу для температурной зависимости вязкости жидкости предложил Я.И.Френкель.
Из (9) следует, что коэффициент вязкости жидкости при повышении температуры уменьшается. Зависимость логарифма вязкости 
от 
, согласно(9), является линейной.
Экспериментальные исследования действительно приводят к такому результату, однако только в небольшом температурном интервале.
Цель лабораторной работы.
Изучить температурную зависимость коэффициента вязкости жидкости и определить энергию активации самодиффузии.
Работа выполняется с использованием капиллярного вискозиметра.
Порядок выполнения работы.
1.С помощью капиллярного вискозиметра определяют коэффициент вязкости исследуемой жидкости при комнатной температуре, а затем, нагревая жидкость в термостате, определяют ее коэффициент вязкости через каждые 
. Нагрев осуществляется до 
С.
2. Провести вычисление коэффициентов вязкости при разных Т, воспользовавшись зависимостью
(10)
полученной из формулы Пуазейля. Здесь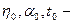 
коэффициент вязкости, плотность, время истечения определенного объема известной жидкости (например, воды). Значения 
берутся из таблиц. Отношение 
есть параметр прибора и не зависит от того, с помощью какой жидкости оно находится.
|
|
|
Измерения 
выполнить 7 раз и провести расчеты 
по средним значениям с нахождением доверительного интервала.
3. Построить графическую зависимость (Т) с указанием на графике доверительного интервала.
4. Из полученной зависимости (Т) можно определить энергию активации q. Для этого прологарифмируем выражение (9)
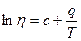(11)
Построить по полученным значениям графическую зависимость от . Если температурный интервал мал, то, очевидно, эта зависимость будет линейной. Тангенс наклона этой прямой дает значение 
5. Определить погрешность, определенной таким образом, Энергии активации.
Контрольные вопросы:
1. Что такое вязкость? Объясните механизм возникновения вязкости в жидкостях. Сравните с механизмом вязкости в газах. Запишите общее уравнение переноса применительно к явлению вязкости.
2. Как зависит вязкость жидкости от температуры? Какой формулой достаточно хорошо описывается зависимость динамической вязкости жидкости от температуры? Чем объяснить различную зависимость вязкости жидкостей и газов от температуры?
3. На чем основан метод измерения вязкости жидкости в данной работе? Для какого течения жидкости выполняется закон Пуазейля? Запишите формулу Пуазейля. Применим ли этот метод для очень вязких жидкостей?
4. Как устроен капиллярный вискозиметр? Чем создается разность давлений на концах капилляра? Почему в вискозиметр необходимо наливать одинаковые объемы как исследуемой, так и стандартной жидкости?
5. С какой целью коэффициент вязкости определяет относительным методом? Как изменяется при этом точность измерений? Получите расчетную формулу для коэффициентов вязкости жидкости капиллярным вискозиметром. Какое условие должно быть выполнено, чтобы к моменту начала измерений течение жидкости, вытекающей из определенного объема, приобрело стационарный характер?
6. Оцените точность измерений. Какие из величин, входящих в расчетную формулу, будут вносить наибольший вклад в ошибку результата?
Литература:
1. Физический практикум под редакцией В.И. Ивероновой. Механика к молекулярная физика. -М., Наука, 1967.
2. А.Н.Матвеев. Молекулярная физика. -М.. Высшая школа, 1961, §50, 51, 52, 56.
3. И.К. Кикоин, А.К. Кикоин. Молекулярная физика. -М.; Наука, 1976, гл. III, §48, 49; гл. VII, §96.
4. С.Э. Хайкин. Физические основы механики. -М., Физматгиз, 1963, §127
Лабораторная работа №8
|
|
|
