Модели нестационарных случайных процессов электропотребления

 

Нестационарные случайные графики нагрузки некоторых электроприемников, участвующих в технологическом процессе, имеют особенности, упрощающие их анализ и моделирование. Эти особенности обусловлены повторяемостью технологических или суточных циклов, сезонными изменениями и др. Результаты измерений таких графиков нагрузки или временные ряды электропотребления можно представить нестационарным случайным процессом, все реализации которого имеют общий детерминированный тренд. Для описания таких процессов не всегда требуется усреднение по ансамблю реализаций, а многие важные свойства можно оценить по одной реализации, как в случае эргодических стационар­ных процессов.

Некоторые типы нестационарных случайных процессов можно моделировать с помощью мультипликативной и аддитивной моделей.

(1.19)

Мультипликативная модель нестационарного случайного процесса представляется следующим образом:

Y(t)=B(t)X(t),

где B(t)- детерминированная функция; X(t)- стационарный случайный процесс с независящим от времени нулевым средним значением и единичной дисперсией.

(1.20)

Аддитивная модель нестационарного случайного процесса имеет вид.

Y(t)=A(t)+X(t),

где A(t) - детерминированная функция (тренд), которая может быть представлена суммой элементарных слагаемых :

A(t)= ;

X(t) - стационарный случайный процесс с независящим от времени нулевым средним значением.

(1.21)

В других работах используется также модель, объединяющая свойства моделей (1.18) и (1.19),

Y(t)=A(t)+B(t)X(t),

где A(t) и B(t) имеют тот же смысл, что и в (1.19), (1.20).

Наиболее широко в электроэнергетике применяется аддитивная модель (1.20), модели же (1.19) и (1.21) имеют ограниченное применение.

Аддитивная модель используется для описания суточных, недельных, годовых графиков электрической нагрузки в прогнозных моделях. Для выделения и моделирования трендовой составляющей используются раз­ложения A(t) в ортогональном базисе.

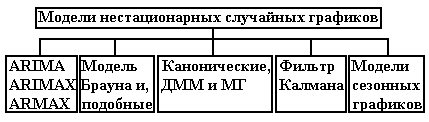
Рисунок 3.3 Классификация моделей нестационарных графиков электрической нагрузки

Классификация моделей нестационарных графиков электрической нагрузки представлена на рис. 1.6. В работе используются три типа из представленных в данной классификации моделей, а именно, модели временных рядов (ARIMA, ARIMAX, ARMAX); канонические ортогональные разложения, в частности, декомпозиционный метод моделирования (ДММ), методы типа “Гусеница” и модели типа Брауна (экспоненциального сглаживания (модель Брауна), модель Хольта и др.).

(1.22)

В задачах прогнозирования и управления широко используются параметрические модели авторегрессии-скользящего среднего (АРСС или ARMA - Auto Regression Middle Average), которые также называются моделями Бокса-Дженкинса:

где ^_ среднее значение процесса (математическое ожидание); - параметры процесса (модели).

Данная модель используется при решении задач прогнозирования электропотребления в системах электроснабжения и в энергетических системах. Для исключения нестационарного тренда из процесса в модель (1.22) вводится также разностный оператор. Такая модель называется моделью авторегрессии - проинтегрированного скользящего среднего (АРИСС или ARIMA - Auto Regression Integrated Middle Average).

Для учета внешних факторов, влияющих на процесс Y(t), в модель вводится вектор внешних факторов X (модели ARMAX, ARIMAX). Модель типа (1.22) используется также при моделировании псевдослучайных последовательностей с заданными характеристиками (КФ и спектральной плотностью).

Для повышения качества и устойчивости, прогнозных АРИСС-моделей путем снижения порядка разностного оператора применяется прием вычитания тренда, получаемого по коэффициентам ортогонального разло­жения.

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: