Многомерное моделирование на основе метода главных компонент

 

Многомерное моделирование на основе метода главных компонент (МГК) можно разделить на следующие этапы:

1. Представление исходных данных наблюдений.

Пусть имеется матрица наблюдений Х, порядка (n N), в которой N столбцов соответствует N исследуемым объектам, а n строк соответствует n переменным, характеризующим эти объекты:

(2.5)

переменные (признаки)

объекты

Будем обозначать через i -ю строку матрицы X, т.е. i -й N -мерный вектор-строку (i=l,2,...,n). Следовательно, - это вектор строка, соответствующая i- й переменной для N объектов.

Столбцы матриц X размерности (nxN), представленной в виде (2.5), есть координаты N точек (объектов) в n- мерном пространстве переменных (признаков). Эти N точек в n -мерном пространстве можно рассматривать как выборку из распределения случайного n -мерного вектора X. Таким образом, j -й столбец матрицы X - это n -мерный вектор (j=l,2,...,N).

Исследуются реализации случайных графиков электрической нагрузки (t), в которых j является номером реализации, a P_j(t_i)=p_ij представляет значение мощности в сечениях (рис. 2.1). Таким образом, в качестве объектов выступают реализации графиков, а параметрами являются значения мощности в сечениях t. решетчатой модели (рис. 2.1,а) или ординаты ступенчатой модели (рис. 2.1,6). Результаты измерений и моделирования можно представить в виде матрицы наблюдений:

сечение ;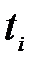

реализации

(2.6)

,j=1,2,…,N.

Рис. 3.4 Представление графиков электрической нагрузки в моделях многомерного статистического анализа: а - реализация решетчатых моделей графиков 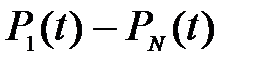;б – ступенчатые модели графиков

 

Столбцы матрицы Р являются дискретными реализациями j -ro графика нагрузки (t), а строки - это совокупности значений реализаций для i -ro сечения. Следовательно, совокупность N решетчатых или ступенчатых моделей графиков нагрузки с n ступенями (n сечениями) можно представить как векторное пространство L_n /11/, элементами (точками) которого являются значения реализаций графиков в сечениях (строки матрицы P), т.е. параметры графиков.

В зависимости от целей исследования матрицы исходных данных X, Р используются непосредственно, либо преобразуются в матрицы центрированных Y /4/ или нормализованных Z /11/ данных.

В матрице Y элемент определяется следующим образом:

где - среднее значение i -й переменной для N объектов (i=1,2,…,n).

В матрице нормализованных данных Z элементы определяются:

(2.7)

Где - дисперсия i -й переменной для N объектов.

Нормализация данных используется в тех случаях, когда размерности компонент векторов X_i различны /4/.

2) Ортогональное преобразование для центрированных данных.

(2.8)

Ковариационная матрица K_Y для матрицы центрированных данных Y определяется следующим образом:

K_Y=YY^T/(N-1),

где Y^T - транспонированная матрица Y.

Для перехода к отображению N объектов в новом n -мерном пространстве с ортогональными переменными, которые называют также факторами /11,13/, необходимо выполнить ортогональное преобразование (вращение в n -мерном пространстве факторов). Предварительно необходимо определить собственные числа и собственные векторы ковариационной матрицы К_у /11/.

Далее собственные числа упорядочиваются в порядке убывания следующим образом:

.

В таком же порядке располагаются соответствующие собственным числам собственные векторы в матрице собственных векторов U.

(2.9)

По полученным собственным векторам выполняется следующее ортогональное преобразование:

Y=UF, ,

где U - матрица (n п) собственных векторов ковариационной матрицы K_Y; F - матрица новых ортогональных переменных для N объектов.

Для любого элемента вектора Y_j или матрицы Y можно записать следующее выражение:

если Y_j- это n -мерный случайный вектор, то матрица U является детерминированной и состоит из n линейно независимых векторов-столбцов. Матрица U является орто-нормированной, т.е.:

U=E, U =E,

где Е - диагональная единичная матрица.

По матрице U и диагональной матрице собственных чисел :

можно воспроизвести ковариационную матрицу K_Y:

или

(2.10)

откуда

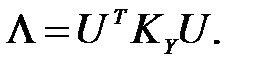
Сумма диагональных элементов матрицы или ее след равен следу матрицы К_у, в соответствии с выражением (2.10). И этот след равен суммарной дисперсии всех n переменных (векторов) Y_j, т.е. сумме дисперсий строк матрицы Y:

(2.11)

Произведение собственных чисел матрицы равно определителю матрицы :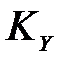

(2.12)

.

В матрице F(n N) N столбцов соответствуют N объектам в новом n -мерном пространстве переменных (факторов, признаков).

(2.13)

новые ортогональные переменные .

Объекты

Новые переменные матрицы (2.13) являются взаимно некоррелированными, т.е. ковариационная матрица является диагональной:

(2.14)

(2.15)

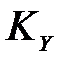Между ковариационными матрицами: , полученной в соответствии с (2.10), и , полученной в соответствии с (2.14), существуют следующие соотношения:

Выражение (2.15) описывает преобразование подобия симметричной матрицы 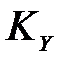путем ее диагонализации.

(2.16)

Элементы матрицы F получаются из обратного преобразования:

Для любого элемента вектора или матрицы F можно записать следующее выражение:

Эффективность каждого признака , т.е. его полезность с точки зрения моделирования Y_j, определяется соответствующим собственным числом . Если некоторый признак (i -я строка в матрице F или i -я компонента вектора F _j) исключается из разложения (2.3), то квадрат среднеквадратической ошибки моделирования Y_j увеличивается на .

Если выполнить разложение (2.3) по m<n компонентам, то абсолютная (m)и относительная среднеквадратические ошибки разложения будут равны:

(2.17)

Собственные векторы ковариационной матрицы 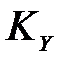дают наименьшее значение среднеквадратической ошибки (m)среди всех возможных ортонормированных базисных векторов.

Собственные векторы являются новыми координатными осями, а векторы - проекциями векторов Y_j на эти новые оси.

Если в качестве ортогональных функций выбираются функции разложения Фурье, для нестационарных и непериодических процессов ко­эффициенты разложения Фурье становятся линейно-зависимыми, что уменьшает их информативность в смысле классификации и требует увеличения размерности признакового пространства.

Как известно, ковариационная матрица 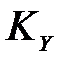является положительно полуопределенной или неотрицательно определенной, т.е. ее собственные числа неотрицательны и могут иметь нулевые значения. Нулевые значения X_i имеют вырожденные матрицы 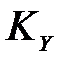, т.е. матрицы с определителем, равным нулю, det(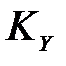)=0 (см. (2.12)).

Характеристическое уравнение, определяющее значения собственных чисел det( E- 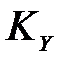)=0, может иметь r<n нулевых корней, а ранг матрицы 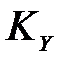соответственно равен n-r.

Собственные числа и соответствующие им собственные векторы упорядочиваются по описанному выше правилу:

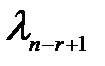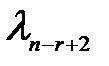> >…> > = =…= =0

В этом случае векторы объектов Y_j, j=1,2,...,N после преобразования (2.3) отображаются в подпространство размерности (n-r): L_n-r<L_n с базисными векторами , j=1,2,...,n-r, которые соответствуют ненулевым собственным числам матрицы 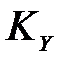, ,…, [4]. Векторы новых переменных (факторов) имеют n-r компонент.

3) Преобразование для матрицы нормализованных данных Z.

Для матрицы нормализованных данных Z, элементы которой определяются по формуле (2.7), вычисляется корреляционная матрица R_z порядка (n n):

(2.18)

Для матрицы R_z, имеющей вид (2.18), вычисляются диагональная матрица собственных чисел и матрица собственных векторов U. Числа и соответствующие им векторы упорядочиваются , ,…, .

(2.19)

Векторы матрицы Z можно разложить по ортогональным составляющим (главным компонентам), аналогично разложению (2.9) матрицы центрированных данных Y, следующим образом:

Z=UF,

где F - матрица ненормированных главных компонент. Для перехода к нормированным компонентам необходимо выполнить преобразование матрицы F в матрицу нормированных главных компонент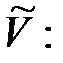

= F,F=

Тогда выражение (2.19) примет вид:

(2.20)

Z=U = A или = A

(2.21)

где

А=U

—матрица, называемая факторной структурой.

(2.22)

Из (2.20) и (2.21) можно получить выражение для нормированных главных компонент:

= или = Z,

где - матрица новых переменных (факторов) для N объектов, элементы которой, имеют тот же физический смысл, что и переменные в разложении (2.9).

Для любого элемента вектора или матрицы в соответствии с (2.22) можно записать следующее выражение:

i=l,2,...,n; j=1,2,...,N.

Элемент матрицы Z в соответствии с (3.20) можно представить следующим образом:

В данном выражении - это вес k -й компоненты в i -й переменной.

Можно также сказать, что А - это матрица коэффициентов корреляции между главными компонентами _; и переменными Z_k (i=1,2,...,n; k=1,2n), т.е. - это коэффициент парной корреляции переменной (фактора) Z_k и
компоненты f_i: a_ki = .

Следовательно, с помощью элементов факторной структуры А определяются переменные (факторы, признаки) Z_k, наиболее тесно связаны с главными компонентами .

Вклад i -й компоненты в общую дисперсию n компонент определяется как норма вектора А _i и равен собственному числу :

(2.23)

По матрице модели А можно воспроизвести матрицу коэффициентов корреляции R_z и диагональную матрицу собственных чисел :

.

Из (2.23) следует, что столбцы матрицы А ортогональны, но не ортонормированы.

Так как на главной диагонали матрицы R_z стоят единицы, то формула (2.11) в данном случае примет вид:

(2.24)

tr(R_z)=tr()=n.

В соответствии с (2.24) сумма диагональных элементов всегда равно целому числу n.

Таким образом, применение разложения (2.9) в виде (2.19) к матрице Z дает другие собственные векторы U и, следовательно, другие признаки F и V, чем при применении этого же разложения (2.9) к матрицам X или Y.

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: