Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы

Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы

Основные источники:

1. Сетков, В. И. Техническая механика для строительных специальностей [Текст]: учеб. пособие / В. И. Сетков. - 3-е изд., стер. - М.: Академия, 2011. - 384 с.

2. Сетков, В. И. Сборник задач по технической механике [Текст]: учеб. пособие / В. И. Сетков. -6-е изд., стер. - М.: Академия, 2011. - 224 с.

Вереина, Л. И. Техническая механика [Текст]: учебник / Л. И. Вереина, М. М. Краснов. - 3-е изд. - М.: Академия, 2011. - 288 с.

3. Олофинская, В. П. Техническая механика: Курс лекций с вариантами практических и тестовых заданий [Текст]: учеб. пособие / В. П. Олофинская. -3-е изд. – М.: Форум: Инфра-М, 2010. - 349 с.

4. Сафонова, Г. Г. Техническая механика [Текст]: учебник / Г. Г. Сафонова, Т. Ю. Артюховская, Д. А. Ермаков. - М.: ИНФРА-М, 2010. - 320 с.

5. Мовнин, М. С. Основы технической механики [Текст]: учебник / М. С. Мовнин; под ред. П. И. Бегуна – 4-е изд. перераб. и доп. – СПб: Политехника, 2007. - 286 с.

Дополнительные источники:

1. Олофинская, В. П  Детали машин. Краткий курс и тестовые задания: [Текст] учеб. пособие / В. П. Олофинская. -2-е изд., испр. и доп. – М. Форум, 2008. - 208 с.

2. Олофинская, В. П. Техническая механика. Сборник тестовых заданий [Текст]: учеб. пособие для СПО / В. П. Олофинская – М.: Форум: Инфра-М, 2002. - 132 с.

3. Эрдеди, А. А. Техническая механика. Теоретическая механика. Сопротивление материалов [Текст]: учеб для машиностроит. спец. техн. / А. А. Эрдеди, Ю. А. Медведев, Н. А. Эрдеди. -3-е изд. перераб. и доп. – М.: Высш. шк., 1991. -304 с.

4. Техническая механика, основы технической механики [Электронные ресурс]. – http: //www. ostemex. ru

Последовательность решения задачи

1. Определяют опорные реакции балки (см. порядок решения задачи практической работы 2).

2. Обозначают характерные сечения (точки) балки. Ими явля­ются концевые сечения балки, опоры, точки приложения сосре­доточенных сил и моментов, начало и конец распределенной на­грузки.

3. Строят эпюру поперечных сил Q_x. Для этого определяют значения поперечных сил в характерных точках. Напомним, что поперечная сила в сечении равна сумме проекций всех сил, рас­положенных только слева или только справа от рассматриваемо­го сечения, на ось, перпендикулярную оси элемента. Силу, рас­положенную слева от рассматриваемого сечения и направ­ленную вверх, считают положительной (со знаком «плюс»), а на­правленную вниз — отрицательной (со знаком «минус»). Для правой части балки — наоборот.

В сечениях, соответствующих точкам приложения сосредото­ченных сил, в том числе в точках приложения опорных реакций, необходимо определить два значения поперечной силы: чуть ле­вее рассматриваемой точки и чуть правее её. Поперечные силы в этих сечениях обозначаются соответственно Q^леви Q^прав.

Найденные значения поперечных сил в характерных точках от­кладываются в некотором масштабе от нулевой линии. Эти значе­ния соединяются прямыми линиями по следующим правилам:

а) если к участку балки нет распределенной нагрузки, то под этим участком значения поперечных сил соединяются прямой линией, параллельной нулевой линии;

б) если на участке балки приложена распределенная нагруз­ка, то под этим участком значения поперечных сил соединяются прямой, наклонной к нулевой линии. Она может пересекать или не пересекать нулевую линию.

Соединив все значения поперечных сил по указанным прави­лам, получим график изменения поперечных сил по длине бал­ки. Такой график называется эпюрой Q_x.

4. Строят эпюру изгибающих моментов М_х. Для этого опреде­ляют изгибающие моменты в характерных сечениях. Напомним, что изгибающий момент в рассматриваемом сечении равен сум­ме моментов всех сил (распределенных, сосредоточенных, в том числе и опорных реакций, а также внешних сосредоточенных моментов), расположенных только слева или только справа от этого сечения. Если любое из перечисленных силовых воздейст­вий стремится повернуть левую часть балки по часовой стрелке, то оно считается положительным (со знаком «плюс»), если про­тив — отрицательным (со знаком «минус»), а для правой части наоборот.

В сечениях, соответствующих точкам приложения сосредото­ченных моментов, необходимо определить два значения изги­бающего момента: чуть левее рассматриваемой точки и чуть пра­вее её. Изгибающие моменты в этих точках обозначаются соот­ветственно М^лев и М^прав. В точках приложения сил определяется одно значение изгибающего момента.

Полученные значения откладываются в некотором масштабе от нулевой линии. Эти значения соединяются в соответствии со следующими правилами:

а) если на участке балки нет распределенной нагрузки, то под этим участком балки два соседних значения изгибающих момен­тов соединяются прямой линией;

б) если к участку балки приложена распределенная нагрузка, то под этим участком значения изгибающих моментов для двух соседних точек соединяются по параболе.

Парабола имеет выпуклость в сторону действия нагрузки (при действии нагрузки сверху парабола обращена выпуклостью вниз). При этом, если эпюра Q_x на рассматриваемом участке не пересе­кает нулевую линию, то эпюра М_х (она является параболой) мо­жет быть построена по двум точкам, так как все значения изги­бающих моментов в промежуточных точках находятся между зна­чениями в характерных сечениях. Если эпюра Q_x пересекает нуле­вую линию, то под этим сечением эпюра М_х будет иметь экстре­мальное (максимальное или минимальное) значение или вершину параболы. Положение этой точки находят по эпюре из подобия треугольников (см. пример 9). Затем находят значение из­гибающего момента в этом сечении и строят эпюру М_х на участке с распределенной нагрузкой по трем точкам.

Соединив все значения изгибающих моментов по указанным правилам, получают график изменения изгибающих моментов по длине балки. Такой график называется эпюрой М_х.

Приведенный способ построения эпюр Q_x и М_х назовем спо­собом построения эпюр по характерным сечениям. Такой спо­соб является частным случаем более общего, хотя и более трудо­емкого способа, который называется способом построения эпюр по участкам. Порядок построения эпюр при этом способе сле­дующий. Балку разбивают на участки. Границами участков явля­ются характерные сечения. Для каждого участка записывается закон изменения усилий Q_x и М_х и определяются их величины при граничных значениях. По найденным величинам усилий строят соответствующие эпюры.

Существует несколько способов проверки правильности по­строения эпюр. Наиболее простой способ проверки заключается в том, что суммы моментов всех левых и всех правых сил, взятые отдельно, в любой точке балки должны быть равны между собой.

5. Подбирают сечение стальной балки в следующем порядке:

а) определяют требуемый момент сопротивления сечения балки:

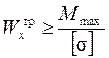
где  М_max — наибольший по абсолютному значению изгибающий момент, принимаемый по эпюре М_х;

[σ ] — допускаемое нормальнее напряжение для материала балки;

б) по ГОСТам прил. I подбираем номер двутавровой стальной балки, которая должна иметь момент сопротивления W_x, наибо­лее близкий по значению к требуемому моменту сопротивления

6. Проверяют прочность принятой двутавровой балки по нормальным напряжениям. Такую проверку выполняют для сечения с наибольшим изгибающим моментом:

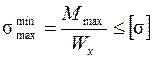
где W_x — момент сопротивления принятого сечения.

Если условие удовлетворено, прочность балки по нормальным сечениям считается обеспеченной, и наоборот.

7. Строят эпюру нормальных напряжений σ . Для этого вычерчивают крупно поперечное сечение балки и проводят на отдельном рисунке нулевую линию перпендикулярно нейтральной оси. Затем на уровне крайних точек сечения (верхней и нижней) от­кладывают найденные ранее значения σ _mах и σ _min и соединяют эти значения прямой линией. Полученный график называется эпюрой σ. Значения σ _mах и σ _min откладывают по разные стороны от нулевой линии.

8. Проверяют прочность принятой двутавровой балки по каса­тельным напряжениям. Наибольшие касательные напряжения возникают в том сечении по длине балки, в котором действует наибольшая поперечная сила (по абсолютному значению), а по высоте сечения — на уровне нейтрального слоя.

Для определения этих напряжений действительное сечение двутавровой балки упрощают: полка и стенка принимаются пря­моугольными: полка с размерами b и t, а стенка — d и (h — 2t). Размеры b, t и h берутся по ГОСТу (прил. I). Таким образом, се­чение двутавровой балки теперь состоит из трех прямоугольни­ков.

Касательные напряжения на уровне нейтрального слоя опре­деляют по формуле Журавского:

,

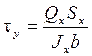где Q_x — поперечная сила в рассматриваемом сечении балки;

S_x — статический момент сечения, расположенного выше или ниже нейтральной оси:

;

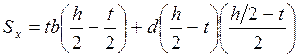J_x — момент инерции всего сечения, принимается по табл. 3 прил. I;

b — ширина сечения балки на уровне нейтрального слоя (см. там же).

Проверяют прочность балки по касательным напряжениям

τ _у ≤ [σ ]

где [σ ] — допускаемое нормальнее напряжение для материала балки.

9. Строим эпюру касательных напряжений. Касательные напря­жения изменяются по высоте балки по криволинейному закону и имеют скачок в месте соединения полки и стенки. Поэтому эпю­ру τ строят по значениям, найденным в пяти точках сечения: крайних точках, на уровне нейтральной оси и на уровне сопря­жения стенки и полки — чуть ниже и чуть выше этого сопряже­ния.

Напряжение в этих точках определяется по формуле Журавского. При этом статический момент S_x и ширина сечения b оп­ределяются для каждой точки сечения. Касательные напряжения в крайних точках сечения равны нулю

Пример 15. Для балки на двух опорах, показанной на рис. 33, а, определить  опорные реакции, проверить правильность определения реакций. Определить значения внутренних поперечных сил в характерных сечениях балки. Построить эпюру поперечных сил. Определить значения внутренних изгибающих моментов в характерных сечениях балки. Построить эпюру изгибающих моментов. Подобрать рациональное сечение двутавровой балки, если [σ ] = 160 МПа. Проверить прочность выбранного сечения по нормальным и касательным напряжениям. Построить эпюру касательных напряжений.

⇐ Предыдущая14151617181920212223Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: