 |
Решение.. Составление отчёта
|
|
|
|
Решение.
1. Определим опорные реакции балки. Составим уравнения:

Из первого уравнения найдем VB:


или –15· 2 + 20· 6· 2 - VB · 7 -25 = 0,
откуда  кН.
кН.
Из второго уравнения найдем VA:

или –15· 9 – 20· 6· 5 + VА · 7 – 25 = 0,
откуда  кН.
кН.
Выполним проверку:

или 108, 6 + 26, 4 – 15 – 20 · 6 = 0,
откуда 135 – 135 = 0.
2. Обозначим характерные сечения балки С, D, А, Е, В, К.
3. Строим эпюру Qx. Определим значения поперечных сил в характерных сечениях:
QC = –F = –15 кН;
QD = –F = –15 кН;
 кН;
кН;
 кН;
кН;
 кН;
кН;
 кН;
кН;

Соединим полученные значения прямыми линиями (рис. 33, б) и получим эпюру Qx. Эпюра Qx на участке АЕ пересекает нулевую линию. Определим положение точки, в которой эпюра Qx пересекает нулевую линию. Рассмотрим подобие треугольников HRL и HNS (см. рис. 33, б), откуда HR/HN = HL/HS, или х0/5 = = 73, 6/100, откуда
 м.
м.
Это сечение считается также характерным для эпюры Qx и Мх.
4. Строим эпюру Мх. Определим изгибающие моменты в характерных точках:
 кН м;
кН м;
 кН м;
кН м;
 кН м;
кН м;

= –15 · 5, 68 – 20 · 4, 68 · 2, 34 + 108, 6 · 3, 68 = 95, 4 кН м;
МВ = М = 25 кН м (рассмотрена правая часть балки ВК);
МК = М = 25 кН м.
5. Строим эпюру Мх на участках между характерными точками:
а) на участке CD нагрузки нет, поэтому эпюра Мх — прямая линия, соединяющая значения МС =0и МD = –15 кН м;
б) на участке DA действует распределенная нагрузка, поэтому эпюра Мх — парабола. Так как эпюра Qx на этом участке не пересекает нулевую линию, то парабола не имеет экстремального значения, поэтому величины изгибающих моментов в сечениях D и А соединим кривой, значения которой находятся в интервале –15 кН м... – 40 кН м;
|
|
|
в) на участке АЕ действует распределенная нагрузка, поэтому эпюра Мх — парабола. Так как эпюра Qx на этом участке пересекает нулевую линию, то парабола имеет экстремальное значение (вершину), поэтому эпюру Мх строим по трем значениям:
МА = – 40 кН м; Мх0= 95, 4 кН м и МЕ = 78 кН м;
д) на участке ВК нет нагрузки, поэтому эпюра Мх — прямая линия, соединяющая значения МВ = 25 кН м и МК =25 кН м.
Эпюра Мх построена (рис. 33, в).
В качестве проверки возьмем сумму моментов всех сил относительно точки, расположенной на расстоянии х0 от левой опоры, но рассмотрим правую часть балки:
Mх0= q(c – х0)(с – х0)/2 + VB(с – х0+ d)+ М =
= –20 · 1, 32 · 0, 66 + 26, 4 · 3, 32 + 25 = 95, 3 кН.
Разница в значениях Мх при рассмотрении левых и правых сил возможна из-за округления величин опорных реакций и расстояния х0.
6. Подберем сечение стальной двутавровой балки по наибольшему изгибающему моменту
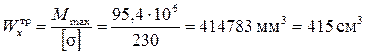 .
.
По табл. 3 прил. I принимаем двутавровую балку №30 с Wx =472 см3, что больше, чем Wxтp =415 см3.
7. Проверим прочность принятого сечения:
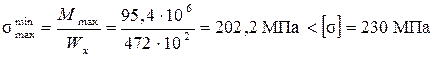 .
.
Прочность сечения по нормальным напряжениям обеспечена.
8. Строим эпюру нормальных напряжений. Отложим от нулевой линии 0—0 (рис. 34, б) значение σ mах = 202, 1 МПа и σ min = 202, 1 МПа и соединим полученные точки. Верхняя часть испытывает сжатие, нижняя — растяжение, так как по эпюре Мх видно, что балка прогибается (обращена выпуклостью) вниз.

Рис. 33
9. Проверим прочность балки по касательным напряжениям. Заменим действительное сечение упрощенным (рис. 34, в). Размеры d =6, 5 мм; t =10, 2 мм; b = 135 мм приняты по табл. 3 прил. I.
Определим наибольшее касательное напряжение
 ,
,
где Qmax = 73, 6 кН;

Jx = 7080 см3;
d = 0, 65см.

Рис. 34
Подставим числовые значения в формулу для τ mах (сечение 1—1):

Проверим прочность сечения по касательным напряжениям:
|
|
|
τ mах = 42, 1 МПа < [τ ] = 130 МПа,
т. е. прочность обеспечена.
В прокатных балках, которые не несут больших сосредоточенных сил в приопорных участках, это условие обычно соблюдается с большим запасом.
6. Построим эпюру τ. Напряжение в сечении 2—2
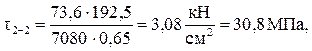
где 
Напряжение в сечении 3—3

где b = 13, 5 см, так как сечение 3—3 проходит по полке.
Напряжение в сечении 4—4 равно нулю, так как Sх = 0. По найденным значениям строим эпюру τ у (рис. 34, г).
Задание для практической работы 11. Для балки на двух опорах, показанной на рис. 7, определить опорные реакции, проверить правильность определения реакций. Определить значения внутренних поперечных сил в характерных сечениях балки. Построить эпюру поперечных сил. Определить значения внутренних изгибающих моментов в характерных сечениях балки. Построить эпюру изгибающих моментов. Подобрать рациональное сечение двутавровой балки, если [σ ] = 160 МПа. Проверить прочность выбранного сечения по нормальным и касательным напряжениям. Построить эпюру касательных напряжений.
Составление отчёта
Практическая работа выполняется в рабочей тетради для оформления практических работ по технической механике. Рисунок и расчётная схема выполняется карандашом. Записи ведутся чётко и грамотно чернилами чёрного или синего цвета. При выполнении практической работы рекомендуется использовать микрокалькулятор. Вариант задания выдаётся преподавателем по списку учебного журнала.
|
|
|


