Последовательность решения задачи

Последовательность решения задачи

К решению задачи рекомендуется приступить после выполне­ния практической работы 4.

1. Определяют положение центра тяжести сечения (см. поря­док решения задачи для практической работы 4).

2. Проводят центральные оси для каждого профиля проката или простой геометрической фигуры. Эти оси называются центральными осями. Для первой фигуры проводят оси х₁и у₂, для второй — х₂и у₂и т. д.

3. Проводят главные центральные оси. Они проходят через центр тяжести всего сечения. Одну из осей совмещают с осью симметрии (в задании все сечения имеют такую ось), а вторую проводят через центр тяжести сечения перпендикулярно первой. Вертикальная ось обозначается v, а горизонтальная — и.

4. Находят моменты инерции сечения относительно главных центральных осей. В общем виде моменты инерции сечения определяют по формулам:

относительно оси и

;

относительно оси v

,

где J_u и J_v — моменты инерции сечения относительно главных центральных осей и и v (главные центральные моменты инер­ции);

J_u^I, J_u^II, …, J_uⁿ — моменты инерции простых фигур (1, 2, ..., п) относительно главной центральной оси и;

J_v^I, J_v^II, …, J_vⁿ — то же, относительно оси v.

Моменты инерции простых фигур относительно осей и и v определяются по формулам:

относительно оси и

;

относительно оси v

,

где J_x1, J_x2, …, J_xn — моменты инерции простых фигур (1, 2, ..., п) относительно собственных центральных осей х₁, х₂,..., х_п. Они определяются по таблицам ГОСТов (см. прил. I) для профи­лей прокатной стали;

J_y1, J_y2, …, J_yn — то же, относительно осей y₁, y₂,..., y_п;

а₁, а₂, ..., а_п -— расстояние от главной центральной оси и до центральных осей х₁, х₂,..., х_п;

b₁, b₂, ..., b_п -— то же, от оси v до осей y₁, y₂,..., y_п;

A₁, A₂, …, A_n, — площади сечений профилей про­катной.

Если главная центральная ось совпадает с собственной цен­тральной осью какого-нибудь профиля или фигуры, то момент инерции ее относительно главной центральной оси равен мо­менту инерции относительно собственной оси, так как расстоя­ние между ними равно нулю.

При определении геометрических характеристик необходимо учитывать, что профили проката на заданном сечении могут быть ориентированы иначе, чем в ГОСТах. Например, верти­кальная по ГОСТу ось у на заданном сечении может оказаться горизонтальной, а горизонтальная ось х — вертикальной. Поэто­му необходимо внимательно следить за тем, относительно каких осей следует брать геометрические характеристики. На это будет обращено особое внимание в рассматриваемых примерах.

Пример 11. Определить моменты инерции сечения, составлен­ного из прокатных профилей, относительно главных централь­ных осей (рис. 27). Сечение состоит из двутавра №33, швеллера №27, двух уголков 90 × 56 × 6 и листа сечением 12 × 180 мм.

Решение.

1. Положение центра тяжести определено в приме­ре 6: у_C = 2, 33 см, если ось проходит через центр тяжести дву­тавра.

2.  Проводим центральные оси для каждого профиля проката х₁, х₂, х₃, х₄и х₅.

3.  Проводим главные центральные оси. Вертикальную ось v со­вмещаем с осью симметрии, а горизонтальную и проводим через центр тяжести сечения С перпендикулярно оси v.

4. Определим момент инерции сечения относительно оси и:

.

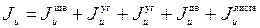Учитывая, что уголки одинаковые и расположены на одинако­вом расстоянии от оси и, получим:

.                                       (а)

Определим величину каждого слагаемого. Момент инерции швеллера №27 относительно оси и

см⁴,

где J_x1^шв = J_у^шв_табл = 262 см⁴ — момент инерции швеллера №27 от­носительно центральной оси х₁, совпадающей с осью у (см. табл. 4 прил. I);

а₁= у₁ – у_С = 14, 63 – 2, 33 = 12, 3 см — расстояние между осями х₁и и;

А_шв = 35, 2 см².

Момент инерции уголка 90× 56× 6 относительно оси и:

см⁴,

где J_х2^уг = J_у^уг_табл = 21, 2 см⁴ — момент инерции уголка 90 × 56 × 6 относительно центральной оси, совпадающей с осью у (см. табл. 2 прил. I);

а₂= у₂ – у_С = 8, 88 – 2, 33 = 6, 55 см — расстояние между осями х₂и и;

А_уг = 8, 54 см².

Момент инерции двутавра №33 относительно оси и:

см⁴,

Рис. 27

где J_х4^дв = J_х^дв_табл = 9840 см⁴ — момент инерции двутавра №33 от­носительно центральной оси х₄, которая совпадает с осью х (см. табл. 1 прил. I);

а₄= у_С = 2, 33 см — расстояние между осями х₄и и;

А_дв = 53, 8см².

Момент инерции листа 12× 180 мм относительно оси и:

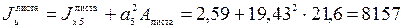см⁴,

где см⁴ — момент инерции листа относительно оси х₅ (см. прил. II);

а₅ = у₅ + у_С = 17, 1 + 2, 33 = 19, 43 см — расстояние между осями х₅и и;

А_листа = 18 · 1, 2 = 21, 6 см².

Подставим полученное значение в формулу (а):

J_u = 5587 + 2 · 388 + 10132 + 8157 = 24652 см⁴.

5. Определим момент инерции сечения относительно оси v:

.                                  (б)

Момент инерции швеллера №27 относительно оси v:

J_v^шв = J_у1^шв = J_х^шв_табл = 4160 см⁴ (см. таб. 4 прил. 1).

Момент инерции уголка 90 × 56 × 6 относительно оси v:

см⁴,

где J_у2^уг = J_х^уг_табл = 70, 6 см⁴ — момент инерции уголка относитель­но центральной оси у₂, которая совпадает с осью х (табл. 2 прил. I);

см — расстояние между осью у₂и осью v;

А_уг = 8, 54 см².

Момент инерции двутавра №30 относительно оси v:

J_v^дв = J_у4^дв = J_у^дв_табл = 419 см⁴ (см. табл. 3 прил. I).

Момент инерции листа 12 × 180 мм относительно оси v:

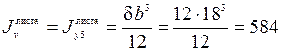см⁴.

Подставим полученные значения в выражение (б):

J_v = 4160 + 2 · 2382 + 419 + 583 = 9926 см⁴.

Ответ: J_u = 24652 см⁴; J_v = 9926 см⁴.

Пример 12. Определить главные моменты инерции сечения, показанного на рис. 28. Сечение состоит из двух уголков 56× 4 и швеллера №18.

Рис. 28

⇐ Предыдущая10111213141516171819Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: