Собственные и примесные полупроводники

Собственными называют полупроводники, не содержащие донорных и акцепторных примесей. Зонная диаграмма таких полупроводников представлена на рис. 4.3,а, где Е_с – нижний энергетический уровень зоны проводимости, называемый дном зоны проводимости; Е_v – верхний энергетический уровень валентной зоны, называемый потолком валентной зоны; DЕ₀ – ширина запрещенной зоны.

Практически чаще пользуются энергетической схемой, изображенной на рис. 4.3,б, где представлены лишь потолок валентной зоны и дно зоны проводимости. Стрелкой обозначен энергетический переход электрона из валентной зоны в зону проводимости, который может быть осуществлен за счет энергии тепловых колебаний решетки или энергии внешнего воздействия на полупроводник. С уходом электрона в зону проводимости в валентной зоне полупроводника остается свободным энергетическое состояние, называемое дыркой, а сама валентная зона становится не полностью заполненной.

Рис. 4.3. Зонная диаграмма собственного полупроводника

В качестве примера собственного полупроводника рассмотрим монокристалл кремния, являющегося элементом IV группы таблицы Д.И. Менделеева. В кристаллической решетке кремния у каждого атома с каждым из четырех ближайших к нему соседей существует ковалентная связь. Плоская модель кристаллической решетки кремния представлена на рис. 4.4, где имеется изображение символа ковалентной связи, в которой участвуют два электрона. При разрыве ковалентной связи между атомами кремния образуются свободный электрон и незавершенная связь, которой на зонной диаграмме соответствует возможное, но не занятое электроном состояние в валентной зоне – дырка. При отсутствии внешнего электрического поля дырка, как и электрон, будет совершать хаотическое движение в пределах кристалла. Происходит это вследствие того, что электрон соседней ковалентной связи за счет энергии тепловых колебаний решетки может заполнить незавершенную ковалентную связь, в результате чего дырка из положения 1 перейдет в положение 2. По этим же причинам она может перейти в положение 3,4 и т.д. Таким образом, движение дырки осуществляется за счет перемещения электрона, участвующего в ковалентной связи.

Итак, в результате разрыва ковалентной связи образуется пара свободных носителей заряда – электрон в зоне проводимости и дырка в валентной зоне, которые и создают собственную электропроводность полупроводника. Энергия, необходимая для разрыва ковалентной связи, определяется шириной запрещенной зоны полупроводника. Для кремния она составляет 1,12 эВ. Свободные носители заряда при комнатной температуре возникают вследствие флюктуаций тепловых колебаний решетки, так как средней тепловой энергии решетки при комнатной температуре для разрыва ковалентной связи в кремнии недостаточно.

 

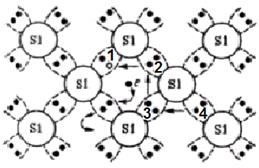
Рис. 4.4. Плоская модель кристаллической решетки собственного полупроводника (кремния)

Примесными называют полупроводники, содержащие донорные и (или) акцепторные примеси.

Если в кремний или германий в качестве примеси ввести элемент V группы таблицы Менделеева, например мышьяк, то атому примеси для завершения ковалентных связей с атомами основного вещества необходимо четыре валентных электрона (рис. 4.5). Пятый валентный электрон атома примеси в ковалентной связи не участвует. Со своим атомом он связан силой кулоновского взаимодействия. Энергия этой связи невелика. Для фосфора, мышьяка, сурьмы она порядка 0,01 эВ в германии и 0,05 эВ в кремнии. Так как при 300 К тепловая энергия kT~0,03 эВ, то очевидно, что при комнатной температуре будет происходить ионизация примесных атомов мышьяка вследствие отрыва пятого валентного электрона, который становится свободным. В германии при 300 К все примесные атомы мышьяка ионизованы. Образовавшиеся при этом положительные ионы примеси принимать участие в электропроводности не могут, так как они локализованы. Находясь в узле кристаллической решетки полупроводника, они являются ее структурными элементами.

 

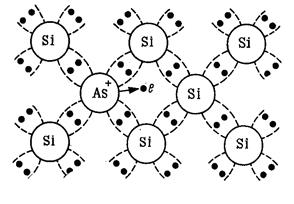
Рис. 4.5. Плоская модель кристаллической решетки полупроводника n-типа (кремния, легированного мышьяком)

Примесь, имеющую валентных электронов больше, чем необходимо для завершения связей между ближайшими атомами основного вещества, и в результате этого способную отдавать электроны, называют донорной, а полупроводник с такой примесью – полупроводником с электронной электропроводностью (или n-типа).

Для того чтобы пятый валентный электрон стал свободным (на энергетической схеме перешел в зону проводимости), необходимо затратить энергию, значительно меньшую, чем для разрыва ковалентной связи. В соответствии с этим энергетический уровень пятого валентного электрона на зонной диаграмме должен располагаться в запрещенной зоне вблизи дна зоны проводимости (рис. 4.6)

 

Рис. 4.6. Зонная диаграмма полупроводника n-типа

При температуре абсолютного нуля и в отсутствие внешнего воздействия на полупроводник его валентная зона полностью заполнена, зона проводимости пуста, локальные энергетические уровни донорной примеси Е_Д заняты электронами. По мере повышения температуры сначала часть электронов, а затем все электроны с локальных уровней Е_Д перейдут в зону проводимости (переходы 1, рис. 4.6). Наряду с этим будут происходить и переходы 2, обусловленные разрывом ковалентных связей, в результате чего образуется пара свободных носителей заряда: электрон и дырка.

Так как для ионизации донорной примеси требуется энергия значительно меньшая, чем для разрыва ковалентной связи (DЕ_Д), то при температурах, при которых собственная электропроводность проявляется слабо, электропроводность полупроводника определяется в основном электронами, образовавшимися при ионизации донорной примеси. Поэтому электроны в полупроводнике n-типа называют основными носителями заряда, а дырки – неосновными носителями.

Если в полупроводник IV группы таблицы Менделеева ввести в качестве примеси элемент III группы, например алюминий, то все три валентных электрона примесного атома будут участвовать в образовании ковалентных связей. При этом одна из четырех связей с ближайшими атомами основного вещества окажется незавершенной.

Примесь, имеющую валентных электронов меньше, чем это необходимо для завершения связей между ближайшими атомами основного вещества, и вследствие этого способную захватить электроны, называют акцепторной, а полупроводник с такой примесью – полупроводником с дырочной электропроводностью (или p-типа).

Незавершенная связь в результате тепловых колебаний решетки может быть заполнена электроном соседней связи, которая в свою очередь окажется незавершенной (рис. 4.7). Незавершенная связь – дырка за счет тепловых колебаний решетки будет совершать хаотическое движение в пределах кристалла. Атом акцепторной примеси, принявший четвертый электрон для завершения ковалентной связи, становится отрицательным ионом. Такой ион называют ионизированным атомом акцепторной примеси. Принимать участие в электропроводности он не может, так как является структурным элементом кристалла.

 

Рис. 4.7. Плоская модель кристаллической решетки полупроводника
р-типа (кремния, легированного алюминием)

Для того чтобы образовалась свободная дырка, необходима энергия меньшая, чем для разрыва ковалентной связи (DЕ_а). В германии и кремнии для бора, алюминия, галлия, индия эта энергия составляет 0,01¸0,07 эВ. Значит, локальные энергетические уровни акцепторной примеси Е_а расположены в запрещенной зоне полупроводника вблизи потолка валентной зоны.

При температуре абсолютного нуля и в отсутствие внешнего воздействия на полупроводник акцепторные уровни свободны от электронов. По мере повышения температуры электроны валентной зоны будут заполнять эти локальные уровни при одновременном образовании в валентной зоне соответствующего числа дырок (рис. 4.8, переходы 1). Вместе с тем возможны и переходы 2, при которых образуется пара свободных носителей: электрон–дырка.

 

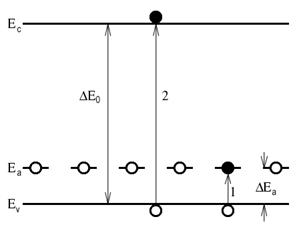
Рис. 4.8. Зонная диаграмма полупроводника р-типа

В полупроводнике р-типа основными носителями заряда являются дырки, неосновными – электроны.

Отметим, что в полупроводниках могут быть примеси, энергетические уровни которых расположены в запрещенной зоне далеко от краев разрешенных зон. Такие уровни называют глубокими. У кремния и германия глубокие уровни возникают при наличии в них примесных атомов золота, меди, кислорода, железа и др.

Рассмотренные зонные модели собственных и примесных полупроводников являются упрощенными, хотя в большинстве случаев они применимы для объяснения физических процессов в полупроводниках и полупроводниковых приборах. Однако есть явления, которые можно объяснить лишь с помощью модели структуры зон, основанной на представлениях квантовой механики с учетом волновых свойств микрочастиц.

4.4. Зависимость концентрации свободных носителей заряда в полупроводниках
от температуры

Как отмечалось, концентрация свободных носителей заряда в полупроводниках увеличивается под влиянием температуры, электромагнитного, ионизирующего излучений и других внешних факторов. Если температура постоянна и никакие другие внешние факторы на полупроводник не воздействуют, то такое состояние называют термодинамически равновесным. В этом случае скорость генерации свободных носителей заряда равна скорости их рекомбинации. Такие носители заряда получили название равновесных. Их концентрации обозначают через n₀ и p₀ (для электронов и дырок соответственно).

Концентрации свободных равновесных носителей заряда в полупроводнике (электронов в зоне проводимости и дырок в валентной зоне) определяются эффективной плотностью энергетических состояний в разрешенных зонах и их фактическим заполнением [2, 5]. Значение эффективной плотности разрешенных состояний определяется с позиций квантовой механики соотношениями неопределенностей Гейзенберга, а вероятность их заполнения – статистической вероятностной функцией Ферми – Дирака [5].

Теория показывает, что в общем виде концентрация свободных электронов в зоне проводимости полупроводника при любой температуре

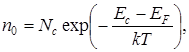(4.1)

а концентрация свободных дырок в валентной зоне

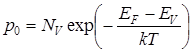, (4.2)

где N_c и N_V – эффективные плотности разрешенных состояний в зоне проводимости и валентной зоне соответственно; E_F – уровень (энергия) Ферми полупроводника (вероятностная характеристика материала), при пересечении уровня Ферми с каким–либо энергетическим уровнем в запрещенной зоне полупроводника вероятность заполнения этого уровня равна 0,5; k – постоянная Больцмана; Т – температура.

Для собственного полупроводника n₀=p₀=n_i. С учетом закона действующих масс

n₀p₀=n_i², (4.3)

концентрация собственных носителей заряда определяется как квадратный корень из произведения (4.1) и (4.2):

. (4.4)

Из (4.1) – (4.3) следует, что концентрация свободных носителей заряда как собственных, обусловленных нарушением ковалентных связей, так и примесных, возникших в результате ионизации атомов примеси, возрастает при увеличении температуры по экспоненциальному закону. Предэкспоненциальные множители N_c и N_v также зависят от температуры, но зависимость эта более слабая – степенная:

. (4.5)

Температурную зависимость концентрации свободных носителей заряда, изображенную на рис. 4.9, рассмотрим на примере полупроводника n-типа. Зависимость в общем виде имеет три участка: 1– примесной проводимости; 2– истощения примеси; 3 – собственной проводимости.

При температуре абсолютного нуля валентная зона полупроводника полностью заполнена, донорные примеси не ионизированы (донорные уровни заняты электронами), зона проводимости пуста. При повышении температуры начинается ионизация донорных атомов и электроны с донорных уровней переходят в зону проводимости (участок 1 рис. 4.9). Чем выше температура, тем больше концентрация свободных электронов в зоне проводимости.

При температуре Т_S все донорные атомы оказываются ионизированными. Повышение температуры от Т_S до T_i на участке 2 рис. 4.9 (участке истощения примеси) не приводит к росту концентрации свободных носителей, поскольку тепловая энергия кТ>DЕ_Д, но еще недостаточна для возбуждения значительной собственной проводимости – нарушения ковалентных связей полупроводника и перехода электронов из валентной зоны в зону проводимости.

 

Рис. 4.9. Температурная зависимость концентрации свободных носителей заряда в полупроводнике n-типа: N_Д1<N_Д2<N_Д3

При температуре T_i на участке 3 рис. 4.9 концентрация электронов, приобретающих энергию, достаточную для перехода из валентной зоны в зону проводимости, превышает концентрацию имеющихся в ней электронов, обусловленных ионизацией донорной примеси. При температурах, больших T_i, в полупроводнике наблюдается собственная проводимость.

Из рис. 4.9 видно, что чем выше концентрация примеси, тем выше концентрация электронов на участках 1 и 2 и тем больше значения температур, соответствующих началу истощения примеси и собственной проводимости. Кривая, изображенная на рис. 4.9 для наибольшей концентрации примеси N_Д3, характерна для так называемых вырожденных полупроводников. У таких полупроводников концентрация свободных носителей заряда вплоть до перехода к собственной проводимости не зависит от температуры, а уровень Ферми находится не в запрещенной зоне, а в зоне проводимости.

Установлено, что в области примесной проводимости (на участке 1 рис. 4.9) от температуры абсолютного нуля до T_S температурная зависимость концентрации свободных электронов имеет следующий вид:

, (4.6)

где N_Д – концентрация донорной примеси; DЕ_Д=Е_с - Е_Д – энергия ионизации донорной примеси; .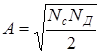

Логарифмируя (4.6), получаем

. (4.7)

Выражение (4.7) является уравнением прямой с отрицательным угловым коэффициентом, пропорциональным DЕ_Д.

На участке 3 при температурах, больших T_i (рис. 4.9), в области собственной проводимости справедливо соотношение (4.4). Если обозначить , после логарифмирования (4.4) получим

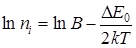. (4.8)

Выражение (4.8) так же, как (4.7), является уравнением прямой с отрицательным угловым коэффициентом. Тангенс угла наклона прямой пропорционален ширине запрещенной зоны полупроводника DЕ₀. Температурная зависимость концентрации свободных носителей заряда в полупроводниках, построенная в координатах , наглядно показывает характер физических процессов, происходящих при изменении температуры, и позволяет рассчитать параметры полупроводникового материала: энергию ионизации донорной примеси DЕ_Д и энергию, необходимую для разрыва ковалентных связей, – ширину запрещенной зоны DЕ₀.

Отметим, что температурная зависимость концентрации свободных носителей заряда – дырок для полупроводника р-типа выглядит аналогично изображенной на рис. 4.9. Интерпретация зависимости на участке примесной проводимости проводится на основе представлений о захвате акцепторными атомами электронов из валентной зоны и об образовании в ней свободных дырок.

Экспоненциальный закон изменения концентрации свободных носителей заряда при изменении температуры обусловливает принципиальное различие между температурной зависимостью проводимости полупроводников и металлов (рис. 4.1). У последних концентрация свободных носителей от температуры практически не зависит.

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: