Приложения определенного интеграла: вычисление площади плоской фигуры (вывод формулы в полярной системе), длины дуги (вывод формулы в ДСК), объема тела вращения относительно Ox (вывод формулы)

Условие интегрируемости функций.

Необходимый признак интегрируемости функции. Если функция f(х) интегрируема на [a,b], то она ограничена на [a,b]. Следствие (достаточное условие интегрируемости): Если функция ограничена и непрерывна на [a,b], всюду кроме конечного числа точек разрыва первого рода, то она интегрируема на этом отрезке [a,b].

2. Свойства определенного интеграла. Теорема о среднем (без док.) Геометрический смысл. Среднее значение функции.

Основные свойства определенного интеграла.

Ø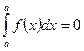

Ø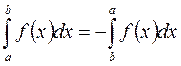

Ø 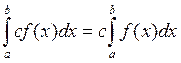,где c-const,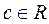

Ø Определенный интеграл от 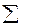функций:

Ø Адитивность определенногоинтеррала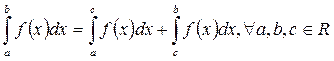

Ø Если 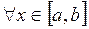, то

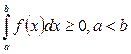
Ø Монотонность определенного интеграла. если , то

Ø Ограниченность.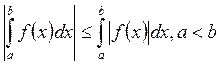

Ø Оценка определенного интеграла. Пусть f(х) интегрируема на [a,b], a<b, ,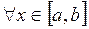

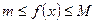
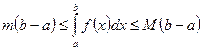
Ø Теорема о среднем: Если f(х) непрерывна на [a,b], то существует точка 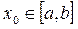, такая что , где 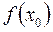-среднее значение.

 

 

3. Классы интегрируемых функций (три теоремы без док.)

Классы интегрируемых функций.

Теорема №1

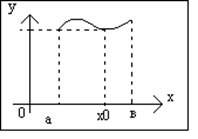
Если 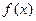определена на [a,в] и непрерывна, то 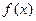интегрируема [a,в].

Теорема №2

Если функция 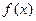монотонна и ограничена на [a,в], то 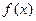интегрируема на [a,в].

Теорема №3

Если ограниченная функция 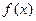на [a,в] имеет конечное число точек разрыва, то 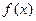интегрируема на [a,в].

4. Теорема об определенном интеграле с переменным верхним пределом (доказать)

Теорема(Борроу): определенный интервал с переменным верхним пределом интегрирования от непрерывной функции f(x) на является первообразной для интегрируемой функции, т.е.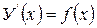

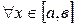
Док-во: дадим аргументу х приращение ,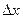

тогда =>/ По Теореме о среднем / ;

то т.д.

 

ГЕОМ.ИЛЛЮСТРАЦИЯ ТЕОРЕМЫ:

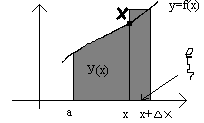
Приращение 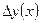= = S криволинейной

трапеции с осями 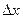, а производная 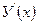=f(х)= длине отрезка х Х.

СЛЕДСТВИЕ: всякая непрерывная функция имеет первообразную.

 

5. Теорема Ньютона-Лейбница (доказать)

Теорема (Ньютона-Лейбница, формула) Если F(х)- есть какая-либо первообразная от непрерывной функции f(х), то справедлива формула: .

Док-во:

С одной стороны F(х) первообразная f(х). С другой стороны по Теореме об определенном интеграле с переменным верхним пределом, 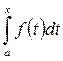- первообразная f(х).

Но любые 2 первообразные от f(х) отличаются на постоянное слагаемое с=const.

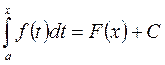
Если х=а, то , но т.к. интеграл с одним пределом равен нулю, => 0=F(a)+C .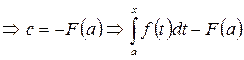

Если х=b,то

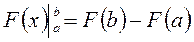,то т.д.

Замечание: Теорема справедлива и для кусочно-непрерывной функции

Теорема об интегрировании по частям (доказать)

Пусть U(x)и V(x) – имеют некоторые первообразные на [a,b], тогда

Док-во: На [a,b] имеет место равенство (UV)’=U’V+UV’

(UV) – первообразная для непрерывной ф-ии (U’V+UV’), тогда по формуле Ньютона-Лейбница:

Теорема об интегрировании методом подстановки (доказать)

Пусть f(x) – непрерывная на [a,b], ф-ия x=φ(t) – непрерывно дифференцируема на [t₁,t₂], причем φ: [t₁,t₂] → [a,b] и φ(t₁)=a φ(t₂)=b тогда

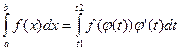
Док-во: Пусть F(x) первообразная для f(x) на [a,b], тогда по формуле Ньютона-Лейбница

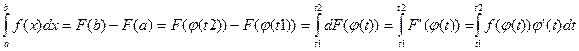
Приложения определенного интеграла: вычисление площади плоской фигуры (вывод формулы в полярной системе), длины дуги (вывод формулы в ДСК), объема тела вращения относительно Ox (вывод формулы)

Площадь в полярной:

За базовую фигуру в полярной системе принимается криволинейный сектор, ограниченный ρ=ρ(φ), φ=α φ=β. Предполагаем, что ρ=ρ(φ) – непрерывна на [α,β]. Для вычисления площади примем алгоритм составления интегральной суммы к последующим предельным переходом к определенному интегралу.

1. Разобьем отрезок [α,β] на n элементарных отрезков α= φ₀< φ₁< φ₂<… < φ_n= β

Δ φ_k = φ_k-1- φ_k

2. На каждом из отрезков [φ_k-1- φ_k] k=1,n выбираем произвольную точку Θ_k и найдем ρ_k=ρ(Θ_k) k=1,n

Каждый криволинейный сектор заменим на круговой сектор с радиусом ρ_k

3. Площадь кругового сектора S_k= 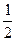ρ²(Θ_k)Δ φ_k

S= 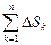= 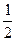ρ²(Θ_k)Δ φ_k

4. За точное значение S_OAB примем интегральную сумму при λ=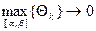

S=

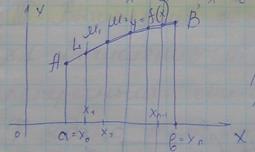Длина дуги в ДСК:

 

Пусть ф-ия y=f(x) определена и непрерывна на [a,b] и кривая L – график этой ф-ии. Требуется найти длину плоской кривой L, заключенной между вертикальными кривыми x = a, x = b

1. Рассмотрим произвольное разбиение [a,b] точками x₀=a, x₁, x₂,…, x_n=b на n частей. Через точку x_k, k=1,n проведем вертикальные линии параллельные O_y до пересечения с кривой L. Дуга AB разбивается на n частей. Соединим соседние точки отрезками и получим ломанную, вписанную в дугу AB.

2. l_n = 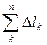l ≈ l_n - ломаная

3. M_k-1M_k – длина стягивающей хорды. Т.к. M_k-1 (x_k-1; f(x_k-1)), Mk (x_k; f(x_k))

Δl = | M_k-1 + M_k| = по теореме Лагранжа

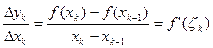ξ_k 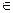[x_k-1, x_k]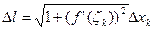

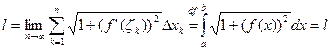
Вычисление объема тела вращения: Рассмотрим тело, образованное вращением вокруг оси Ox криволинейной трапеции aABb ограниченной кривой y=f(x), осью O_x и x = a, y = b

1. Рассмотрим произвольное разбиение [a,b] x₀ = a < x₁< x₂<… < x_n = b

обозначим Δx_k = x_k-x_k-1

2. Пересекаем тело вращения плоскостями перпендикулярными Ox и получи круги, радиусы которых равны |yk|=|f(xk)| На каждом [x_k-1- x_k] выберем произвольным образом ξ_k S(ξ_k)= πf²(ξ_k) (S=πR²)

3. Предположим на любом частном отрезке ф-ия S=S(x) совпадает с S(ξ_k). Тогда объем частичного цилиндра: ΔV_k = S(ξ_k)Δx_k = πf²(ξ_k)Δx_k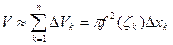

4.

1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: