Понятие частной производной ФНП. Геометрический и физический смысл.

Определение.

Частной производной z'_x функции z=f(x;y) по независимой переменной x называется предел отношения частного приращения функции Δ_xz по переменной x к приращению аргумента Δx при условии, что Δx→0

Геометрический смысл частных производных.

Пусть функция z=f(x,y) определена на плоском открытом множестве G и имеет частный предел (x₀,y₀).

По определению частной производной (x₀,y₀)

_{Частная производная} (x₀,y₀) – есть тангенс угла касательной к графику функции в точке (x₀,y₀,f(x₀,y₀)).

Аналогично геометрический смысл (x₀,y₀) -_{тангенс угла наклона касательной к графику функций}

в точке (x₀,y₀,f(x₀,y₀)).

 

 

Физический смысл частной производной.

Физический смысл состоит в том, что она определяет скорость изменения функции z=f(x,y) в т. (x₀,y₀) в направлении оси х и у.

Понятие дифференцируемой ФНП в точке

Функция у=f(х) называется дифференцируемой в т. x₀, если

Пусть u=f() определена на множестве D и М ()–внутренняя точка D.

Пусть ∆u= – полное приращение функции u=f(u) в т. , отвечающие приращениям

Определение

Функция u=f(M) называется дифференцируемой в т. U () –если ее полное приращение в этой точке имеет вид , где -числа(1,2..n), -бесконечно малое высшего порядка малости, чем .

Понятие полного приращения и полного дифференциала. Геометрическая интерпретация

Полное приращение функции z=f(x;y) в точке (, ) называется разность

Геометрически частные производные можно изобразить отрезками:

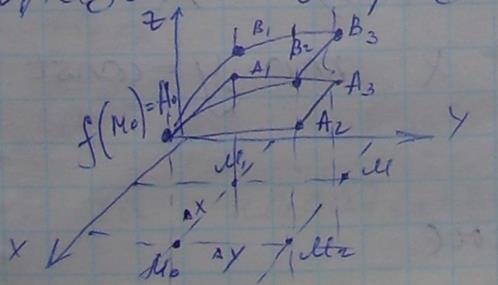
Дифференциалом функции u=f() в т. называется линейная относительно приращений аргументов часть приращения функции.

Обозн.:

С геометрической точки зрения дифференциал представляет приращение ампликаты касательной плоскости (n=2).

 

Свойства дифференцируемой ФНП в точке: теорема о непрерывности дифференцируемой функции и теорема о необходимом условии дифференцируемой функции (2 теоремы – доказать), теорема о достаточном условии дифференцируемости функции и следствие (без док.)

Теорема1(о нопрерывности дифференцируемой функции):

Всякая дифференцируемая функция непрерывна.

Док-во:

Пусть функция z=f(x,y) дифференцируема. Тогда существует

Но , а по определению непрерывности и означает непрерывность z=f(x,y).

Теорема2(необходимое условие дифференцируемости):

Если функция z=f(x,y) дифференцируема в точке (x₀,y₀), то в этой точке существуют частные производные по всем переменным и они равны: ;

Док-во:

Пусть функция z=f(x,y) дифференцируема, т.е.

Вычислим:

Аналогично: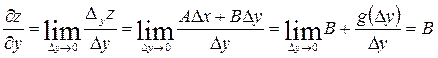

Теорема 3 (достаточное условие дифференцируемости )

Пусть в области D функция z=f(x,y) имеет непрерывные частные производные, тогда функция дифференцируема.

Следствие.

Если функция z=f(x,y) имеет непрерывные частные производные в т. , то она имеет полный дифференциал в т. и в некоторой ее окрестности выполняется равенство:

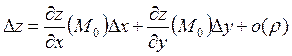,т. е. ; Если ∆х=dx, ∆y=dy, то

24. Понятие неявно заданной функции. Теорема о дифференцируемости неявно заданной функции (без док.) (×)

Функция z=f(x,y) называется неявной, если она задается уравнением F(x;y;z)=0, неразрешенным относительно z. Чтобы найти частные производные дz/дx и дz/дy неявной функции z, заданной уравнением F(x;y;z)=0, нужно подставить вместо z функцию f(x,y), получим тождество F(x;y;f(x;y)) 0. Частные производные по х и по у функции, тождественно равной нулю, также равны нулю.

Теорема1(О существовании, непрерывности, единственности, дифференцируемости неявной функции одного аргумента)

Пусть 1) F(x,y)=0 определена и непрерывна вместе со своими частными производными в некоторой окрестности т. М₀(х₀,у₀)

2) F(x₀,y₀)=0

3) F′_y(x₀,y₀)≠0

Тогда найдется окрестность точки х₀ U(x₀,δ) в этой окрестности существует неявно заданная функция y=f(x) определенная уравнением f(x,y)=0 и такая, что 1)y₀=f(x₀)

2) y=y(x) непрерывна вместе со своими частными производными

F′_x(x,y)

y′= -----------

F′_y(x,y)

Теорема2 (о существовании, единственности, непрерывности и дифференцируемости неявной функции многих переменных):

Пусть выполняется:

1) F(x₁,x₂,x₃,…..,x_n,U) определена и непрерывна вместе со своими частными производными в окрестности M₀т. М₀(x⁰₁,x⁰₂,….,x⁰_n)

2) F(M₀)=0

3) F′_U(M₀)≠0

Тогда найдется такая окрестность M₀ в пределах которой существует неявно заданная функция U(x₁,x₂,x₃,…..,x_n), которая определяется уравнением F(x₁,x₂,x₃,…..,x_n,U)=0, такая что

1) U⁰(x₁⁰,x₂⁰,…..,x_n⁰)

2) U=U(x₁,x₂,x₃,…..,x_n) непрерывна вместе со своими частными производными при чем выполняется:

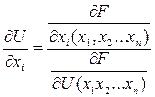
⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: