 |
Три свойства (о линейной комбинации членов) сходящихся рядов (теоремы доказать)
|
|
|
|
Теорема2
Если ряд 
- сходящийся и его сумма равна S,то ряд 
(
0) сходящийся и 
= S
Если ряд 
- расходится,то 
-расходится.
Док-во: Пусть 
- сходящийся. 
= 
= 
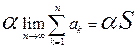
Пусть 
-расходится 
= 
-расходится.
Теорема3
Если ряды 
и 
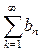- сходится и их суммы соответственно равны 
и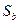 
, то ряд 
также сходится и 
= 
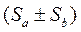
Док-во: 
= 
= 
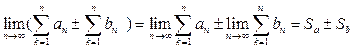
Теорема 4
Если у сходящегося ряда 
отбросить конечное число первых членов,присоединить конечное число членов ряда или произвести перестановку членов ряда, то это не повлияет на сходимость ряда.
Опр-е: Для ряда 
выражение вида 
называется остатком данного ряда после n-го слагаемого.
Если остаток ряда сходится,то 
= 
Теорема 5 (Сходимость ряда 
сходимости его остатка)
Если ряд сходится,то и любой его остаток сходится.Если какой-то остаток ряда сходится,то сам ряд сходится,причем если:
, 
, 
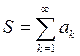,то 
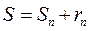
Док-во:
Пусть 
и 
-частичная сумма ряда 
и 
соответственно 
, 
,тогда 
. Для произвольного фиксированного n.
(сходится к ) и 
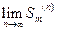(сходится к )сущ-ют и несущ-ют одновременно.
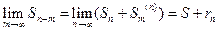
Ряды с неотрицательными членами. Критерий сходимости рядов с неотрицательными членами (теор. док.)
Ряды с неотрицательными членами: Ряд 
все члены которого неотрицательны 
называется знакоположительным.
Критерий сходимости:
Н: Для того, чтобы знакоположительный ряд 
сходился, необходимо и достаточно, чтобы его частичные суммы ограничены сверху (т.е.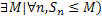 
Доказательство: П. знакоположительный ряд сходится. Это значит 
.
{Sn}- последовательность ч.с. – возрастающая. Тогда Sn<S, т.е. {Sn} – огранич., S=M.
Д: Члены последовательности ч.п.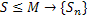 
огранич. сверху. Кроме того 
– возрастающая, монотонно. Поэтому, по теореме Вейерштрасса (всякая монотонная возрастающая, ограниченная сверху последовательность имеет предел): 
– сходится.
|
|
|
Первый признак сравнения (теор. док.)
Если начиная с некоторого номера N (для 
) выполняется неравенство 
, то из сходимости ряда B => сходимость ряда A; из расходимости ряда A => расходимость ряда B.
Доказательство:
Не умаляя общности положим , с n=1. Если ряд B сходится => числовые суммы ограничены (по критерию сх-ти знакопол. рядов), значит ч.с. ряда A и подавно ограничены (т.к. ) => ряд A – сходится. Ряд A расходится, тогда (по критерию сх-ти знакопол. рядов) ч.с. неогранич. => ч.с. ряда B тем более неогранич. => ряд B – расходится.
Предельный признак сравнения (теорему док.)
Пусть имеется два знакоположительных ряда 1) 
2) 
.
Если существует конечный предел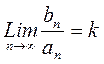 
, то
1) если ряд (1) сходится, 
,то ряд (2) сходится
2) если ряд (1) расходится, ,то (2) расходится.
В частности получаем, если 
, то (1) и (2) либо вместе сходятся, либо расходятся.
Доказательство:
1) По условию теоремы 
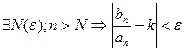
Рассматривая модуль, получим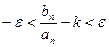 
; 
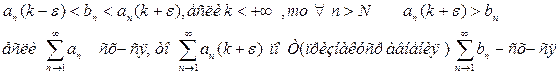
2) k>0, выбираем значения 
,если (1) расходится, то 
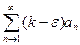, где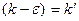 
, 
-расходится (по признаку сравнения).
Признак Даламбера, радикальный и интегральный Коши(3 теоремы док.).
Признак Даламбера.
Пусть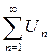 
- ряд с неотрицательными членами.
Если 
, то
а) 
- ряд 
-сходится;
б) 
- ряд 
- расходится;
в) 
- о сходимости ничего нельзя сказать.
3 Эталон: обобщенный гармонический 
; 
Доказательство:
По условию теоремы,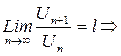 
, начиная с 
будет выполняться условие 
;
а) Пусть 
начиная с :
; 
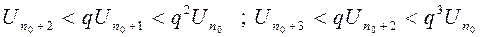
члены исследуемого ряда 
меньше членов геометрической прогрессии 
; Геометрическая прогрессия сходится.
б) ; пусть 
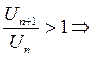для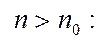 
ряд сходится.
Радикальный признак Коши.
Дан ряд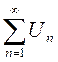 
,если 
, то при
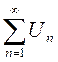а) - ряд -сходится;
б) - ряд 
- расходится;
в) - о сходимости ничего нельзя сказать, предполагается что предел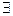 
Доказательство:
По условию теоремы, 
, начиная с 
будет выполняться условие 
; 
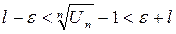
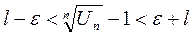
а) 
- убывающая геометрическая прогрессия Þ по признаку сравнения 
- сходится, начиная с .
|
|
|
б) аналогично предыдущему.
|
|
|
