Экстремум ФНП. Теорема о необходимом условии существования экстремума (доказать)

Функция z=f(x,y) имеет max в точке М₀(х₀,у₀), если f(x0,y0)>f(x,y) для любого(х,у), достаточно близких к (.)(х₀,у₀) и отличных от нее.

Функция Z=f(x,y) имеет min в точке М₀(х₀,у₀), если F(x₀,y₀)<f(x,y) выполняется для любых точек (х,у), достаточно близких к точке (х₀,у₀), но отличных от нее.

Точки максимума и минимума функции называются экстремумами функции z=f(x,y); точки в которой частные производные dz/dx=0 dz/dy=0 или не существуют называются критическими.

Т. Если функция z=f(x,y) достигает экстремума при х=х₀, у=у₀, то каждая частная производная первого порядка от Z либо обращается в нуль при этих значениях, либо не существует.

Дадим переменному у определенное значение, именно у=у₀. Тогда функция f(x,y0) будет функцией одного пременного х. Т.к при х=х₀ она имеет экстремум (max или min), то следовательно (dz/dx)_{x=x0 y=y0} или равно нулю или не существует. Аналогично можно доказать, что (dz/dy)_{x=x0 y=y0} или рано нулю или не существует. Замечание: Данное условие не является достаточным условием экстремума в т. Х₀, у_0.

Достаточное условие: Пусть дана функция z=f(x,y)? введем следующие обозначения: a₁₁=d²z/dx² a₁₂=d²z/dxdy a₂₂=d²z/dy² δ=

 

Пусть в некоторой области, содержащей (.) М0(х0,у0) функция z=f(x,y) имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того точка М0 является критической точкой функции z=f(x,y), т.е: (df(x0,y0))/dx=0; (df(x0;y0))/dy=0, тогда при х=х₀, у=у₀:

1) f(x,y) имеет минимум, если a₁₁>0, δ>0 (d²f(x₀,y₀)>0)

2) f(x,y) имеет максимум, если a₁₁<0, δ>0 (d²f(x₀,y₀)<0)

3) функция F(x,y) не имеет ни максимума ни минимума, если δ<0 (d²f(x₀,y₀) меняет знак)

4) если δ=0, то экстремум в точке (х₀,у₀) может существовать, а может и нет

33. Квадратичные формы. Положительно определенная, отрицательно определенная, квазизнакоопределенная, неопределенная квадратичная форма. Достаточное условие существования экстремума в терминах квадратичной формы (сформулировать).

Некоторые сведения о квадратичных формах [к.ф.]

Опр. К.ф. от n-переменных называется функция вида Q(x₁,x₂,…,x_n)=a₁₁x₁²+a₁₂x₁x₂+…+a_1n+x₁x_n+ a_2nx₂x₁+a₂₂x₂²+…+a_2n+x₂x_n+…+a_n1x_nx₁+a_n2x_nx₂+…+a_nnx_n², где а_i,j – действительные числа a_ij=a_ji

Краткая запись

а_i,j – это коэффициенты квадратичной формы и из этих коэффициентов составляют матрицу

матрица квадратичной формы.

Опр. Миноры матрицы образованные строками и столбцами с одинаковыми номерами на главными (угловыми) минорами

Обозначаются , …

Виды квадратичных форм.

		Определение	Примеры
Знако - енные	Положительно определенные	Если для любых значений х1,…,хn≠0 одновременно к.ф. принимает положительные значения	Q(x1,xn)=2x12+3x22
Отрицательно определенные	||~|| Отрицательные значения	Q(x1,xn)=- x12+x1x2- x22
квазизнакоопределенная	Неотрицательная	Если к.ф. принимает неотрицательные значения, но при этом обращается в 0, не только при х1=x2=…=xn=0	Q(x1,x2)=(x1+x2)2 Q=0, при x1= -x2 M(1;-1)
Неположительная	Если к.ф. принимает неположительные значения, но при этом обращается в 0, не только при х1=x2=…=xn=0	Q(x1,x2)=-(x12+2x1x2+x22)= -(x1+x2)2 Q=0, при x1= -x2; M(2;-2)
Квазизнакопеременая	||~||	Если к.ф. принимает как положительные, так и отрицательные значения.	Q(x1,x2)=x12+x22 Q(2,1)=3>0 Q(1,2)=-3<0

Т3. Достаточный признак (условие) локального экстремума (в форме дифференциалов)

Пусть задана функция U=f(x₁,…,x_n) дифференцируема в некоторой окрестности т. М₀ и дважды дифференцируема в т. М₀, и М₀ – стационарная точка du(M₀)=0

Тогда если

1) d²u|_Mo положительно отрицательный к.ф., то М₀ – точка локального минимума

2) если d²u|_Mo – отрицательно определенная квадратичная форма, то М₀ – точка локального максимума.

3) d²u|_Mo – знакопеременная к.ф. то экстремум в точке М₀ отсутствует.

4) d²u|_Mo – квазизнакопеременная к.ф. то в т. М₀ может быть экстремум, может и не быть.

34. Понятие дифференциального уравнения первого порядка, решение ДУ, интегральная кривая, частное решение, начальные условия, задача Коши.

Определение: Дифференциальным уравнением называется уравнение в котором неизвестная функция входит под знак производной или дифференциала.

Если неизвестная функция зависит от одной переменной то диф. ур. называется обыкновенным. Если от нескольких, то диф. ур. частных производных.

Общий вид обыкновенного диф. ур. n-го порядка:

где, F – заданная функция связывающая независимую переменную x, независимую функцию и её производные .

Порядок старшей производной входящей в диф. ур. называется порядком этого уравнения.

Пример:

1. - об.диф.ур. первого порядка относительно неизвестной функции .

2. - об.диф.ур. III порядка относительно неизвестной функции .

3. – диф.ур. 2-го порядка относительно неизвестной функции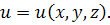

Общий вид обыкн.диф.ур. I-го порядка:

 

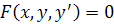
Общим решением диф.ур.(1) 1-го порядка называется функция 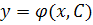(2). От и произвольной постоянной , д.у. (1) в тождество.

Общее решение, заданное в неявном виде 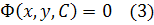называется общим интегралом.

Геометрическое общее решение (общий интеграл) представляет собой семейство интегральных кривых на плоскости, зависящих от .

График решения называется интегральной кривой. Процесс нахождения решения д.у. называется интегрированием д.у.

 

Определение: Частным решением д.у. (1) называется решение полученное из общего решения (2) при фиксированном значении : .

Частный интеграл получается из уравнения (3) при фиксированном значении : .

 

Задача Коши: Найти решение диф.ур. (1) удовлетворяющее заданным начальным условиям при .
35. Теорема о существовании и единственности решения задачи Коши(без док). Определение общего решения ДУ. Особое решение.

Теорема(Коши): (о существовании и единственности решения д.у.):

Пусть заданно д.у. . Если функция и частная производная по 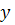непрерывна в некоторой области 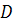плоскости содержащей точку , то найдется интервал на котором существует единственное решение , д.у. (1), удовлетворяющее условию .

– начальные условия. - начальные числа.

Геометрически теорема означает, что через каждую внутреннюю точку проходит единственная интегральная кривая. Т.о. вся область 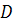, где и - непрерывны, покрыта интегральными кривыми которые никогда не пересекаются.

Определение: Общее решение д.у.(1) называется функция 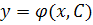, если

1. она является решением д.у.(1) при любом значении ;

2. каковы бы ни были начальные условия можно найти единственное значение такое, что удовлетворяет (1).

Найти решение д.у. значит найти частное решение (интеграл) или общее решение (интеграл).

)

Определение: Решением д.у. (1) называется особым решением если соответствующая интегральная кривая обладает тем свойством, что через любую её точку проходит, кроме неё, ещё и другая касающаяся её интегральная кривая данного уравнения.

Пример: уравнение Бернулли.

Общий интеграл этого уравнения имеет вид:

Проверим условие теоремы: непрерывна на непрерывна в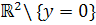

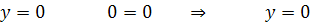решение д.у. (особое решение)

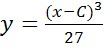
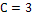
– огибающая семейства интегральных кривых.

 

36. Основные виды ДУ: с разделяющимися переменными, однородные, линейные первого порядка, Бернулли, в полных дифференциалах.

Определение: Д.У. является уравнением с разделяющимися переменными, если его правая часть представляет собой, или может быть представлена в виде произведения(или отношения) 2-х функций, одна из которых зависит только от х, а другая – только от у, т.е.

или или

Решение д.у. с разделяющими переменными осуществляется поэтапно:

1) Пусть исходное уравнение имеет вид

а) Представляем функцию в виде произведения

F(x,y)= и используя различные алгебраические приемы.

b) Заменяем производную отношением 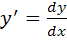.Уравнение примет вид

c) Умножаем обе части уравнения на dx и, одновременно, делим на функцию . Получим 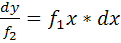. Переменные разделены.

d) Интегрируем обе части полученного уравнения:

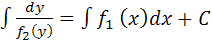
2) Если уравнение задано в неявной форме, то следует из него выразить y’ в явном виде и далее действовать как уже было сказано.

3) Если уравнение задано в форме , то

а) переносим второе слагаемое в правую часть;

b) каждую из двух функций представляем в виде произведения (или отношения) сомножителей.

с) Делим обе части уравнения на произведение функции

d) Общий интеграл находим интегрированием

Определение: Д.У. называется однородным, если его правая часть есть однородная функция своих аргументов

Для преобразования однородного уравнения к виду, с которого начинается использование подстановки, необходимо:

1)выразить в явном виде производную искомой функции из любой исходной формы записи уравнения.

2)преобразовать функцию к виду

3)Сделать замену , которая позволит разделить переменные в полученном уравнении.

К однородным могут относиться уравнения, в которых отношения стоят под знаком какой-либо функции.

 

Определение: Д.У. является линейным, если его правая часть есть линейное выражение относительно искомой функции .

Другими словами: всякое уравнение 1-го порядка будет линейным, если искомая функция и ее производная входят в уравнение в первых степенях и не перемножаются.

Для решения линейных уравнений используют два метода: метод Бернулли (подстановки) и метод Лагранжа (вариации произвольной постоянной)

МЕТОД БЕРНУЛЛИ (метод подстановки):

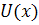Этот метод позволяет с помощью подстановки сводить любое линейное уравнение к двум уравнениям с разделяющими переменными относительно функций и

МЕТОД ЛАГРАНЖА (вариации произвольной постоянной):

Решение линейного уравнения методом вариации состоит из двух этапов:

1) находим общее решение однородного уравнения Получаем функцию , где С- произвольная постоянная.

2) Подставляем функцию в исходное уравнение, находим функцию и записываем общее решение исходного уравнения.

Определение: уравнение является уравнением Бернулли, если правая часть уравнения имеет вид , где 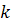– любое рациональное число, исключая случаи и . При уравнение является линейным, а при – с разделяющимися переменными.

Форма уравнения Бернулли: .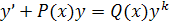

Замечание: Данное уравнение сводится к линейному следующим образом. Сначала делим уравнение на :

а затем делаем замену

Уравнение примет вид и далее решается как линейное, например методом подстановки

Однако, при решении конкретных примеров можно предварительно не сводить уравнение Бернулли к линейному, а сразу решать его как линейное.

Определение: Уравнение является уравнением в полных дифференциалах, если выполняется условие

Интегрирование уравнения в полных дифференциалах проводится следующим образом:

1) Проверяем выполнение условия

2) Если условие выполняется, то левая часть уравнения есть полный дифференциал некоторой пока неизвестной функции , т.е .Тогда в соответствии с уравнением, , и поэтому общий интеграл уравнения в полных дифференциалах запишется в виде .

Таким образом, решение уравнения сводится к нахождению функции .

37.Определение общего решения ДУ порядка выше первого, частное решение.

Д.У. n-го порядка называется уравнение, которое содержит независимую переменную x, искомую функцию у, ее производную n-го порядка.

Уравнение n-го порядка может быть записано в явной форме, если оно разрешено относительно старшей производной , или в неявной

Решение Д.У. n-го порядка называется любая n раз дифференцируемая функция y=y(x), которая при подстановке в уравнение, обращает его в тождество.

Каждое уравнение n-го порядка имеет бесконечное множество решений. Выбрать из этого множества конкретное решение можно, если задать n дополнительных условий, например начальных.

Начальными условиями для уравнений n-го порядка являются задания значений искомой функции и ее производных до (n-1)-го порядка включительно при заданном значении , , , …

Общим решением уравнения называется функция 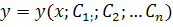, которая удовлетворяет следующим условиям:

1) Функция содержит произвольные постоянные, количество которых равно порядку уравнения;

2) Эта функция является решением уравнения при любых значениях произвольных постоянных;

3) При заданных начальных условиях произвольные постоянные можно определить единственным образом так, что полученное частное решение будет удовлетворять заданным начальным условиям.

Если решение записано в неявном виде, то оно называется общим интегралом этого уравнения.

Всякое решение, которое полученное из общего решения при конкретных значениях, называется частными решениями.

38.Теорема о существовании и единственности решения задачи Коши Д.У. порядка выше первого (без.док.)

Если функция (n+1)-й переменной в некоторой области (n+1)-мерного пространства непрерывна и имеет непрерывные Ч.П. по переменным , (), то для любой фиксированной точки 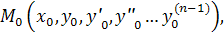этой области и при том единственное решение уравнения .

Определенное на и удовлетворяет начальным условиям , , .

Д.У. 2-го порядка c начальными условиями , . Через точку проходят бесконечно много интегральных кривых, и задаем и выбираем единственную интегральную кривую.

 

 

39. Понятие линейного ДУ n-го порядка (×)

 

Линейным дифференциальным уравнением высшего порядка называется уравнение, в котором искомая функция y(x) и ее производная входят в первых степенях и не перемножаются. Общий вод такого уравнения

a₀y⁽ⁿ⁾+a₁y^(n-1)+ a₂y^(n-2)+…a_ny=f(x), где а₀, а₁, … - либо функция от х, либо постоянные числа.

Линейное дифференциальное уравнение 2-го порядка имеет вид

ay’’+by’+cy=f(x).

Если f(x)=0, то уравнение называется однородным, уравнением без правой части. Если f(x)≠0, то уравнение называется неоднородным, или уравнением с правой частью.

 

40. Однородные линейные ДУ n-го порядка. Две теоремы о свойствах решений ОЛДУ (док.) (×)

a₀y⁽ⁿ⁾+a₁y^(n-1)+ a₂y^(n-2)+…a_ny=f(x) где а₀, а₁, … - либо функция от х, либо постоянные числа.

Если f(x)=0, то уравнение называется однородным, уравнением без правой части.

Пусть a₀y⁽ⁿ⁾+a₁y^(n-1)+ a₂y^(n-2)+…a_ny=0 => у⁽ⁿ⁾ + P₁y^(n-1) +…+ P_n-1 y’ + P_n y = 0 где P_n=a_n/ a₀

1) Если у₁(х) – частное решение ЛОДУ у⁽ⁿ⁾ + P₁y^(n-1) +…+ P_n-1 y’ + P_n y = 0 (2), то функция С *у₁(х), где С=const, также является решением этого ЛОДУ.

Док-во:

Су⁽ⁿ⁾ + P₁Сy^(n-1) +…+ P_n-1 С y’ + P_n С y = 0

С(у⁽ⁿ⁾ + P₁y^(n-1) +…+ P_n-1 y’ + P_n y) = 0

у⁽ⁿ⁾ + P₁y^(n-1) +…+ P_n-1 y’ + P_n y = 0

 

2) Если у₁(х) и у₂(х) – решение ЛОДУ, то функции у₁(х) + у₂(х) также являются решениями этого ДУ

Док-во:

(у₁+у₂)⁽ⁿ⁾ + P₁(у₁+у₂) ^(n-1) +…+ P_n-1 (у₁+у₂)’ + P_n (у₁+у₂) =

= [у₁ ⁽ⁿ⁾ + P₁ у₁ ^(n-1) +…+ P_n-1 у₁’ + P_n у₁] + [у₂ ⁽ⁿ⁾ + P₁ у₂ ^(n-1) +…+ P_n-1 у₂’ + P_n у₂] = 0

 

3)Если у₁(х) и у₂(х)... у_n(х) решение ЛОДУ, то их линейная комбинация С₁ у₁(х) + С ₂у₂(х)... С_n у_n(х) – так же является решение этого уравнения.

 

41. Определитель Вронского. Теорема о равенстве нулю вронскиана линейно-зависимых функций (док.).

Определение: Определитель Вронского (или вронскиан) функций y₁,y₂,…,y_n – это определитель вида:

(где y_1, y_2, y_n - ФСР C₁,C₂,…,C_n - const)

Определителем этой системой является определитель Вронского

Теорема: (Необходимое условие линейной зависимости функции, но не являются достаточным)

Если функции y_1, y_2, …,y_n - линейно зависимы и имеют производные до (n-1) порядка, то их определитель Вронского тождественно равен 0.

Док-во:

Так как y_1, y_2, …, y_n - линейно зависимы, то существуют числа α₁, α₂, …, α_n (то есть все равные нулю одновременно) такие что α₁y₁ + α₂y₂ + …+ α_ny_n = 0 на x 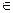(a,b)

Продифференцируем равенство (n-1) раз и получим линейную однородную систему уравнений:

α₁y₁ + α₂y₂ + …+ α_ny_n = 0

α₁y₁’ + α₂y₂’ + …+ α_ny_n’ = 0

α₁y₁’’ + α₂y₂’’ + …+ α_ny_n’’ = 0 =>

……………………………..

α₁y₁^(n-1) + α₂y₂^(n-1) + …+ α_ny_n^(n-1) = 0

Система имеет нетривиальное решение любых Х из (а,b), определитель этой системы – определитель Вронского.

W[y_1, y_2, …,y_n ] = 0 для любых Х из [а,b]

 

42. Теорема о неравенстве нулю вронскиана линейно-независимых решений ЛОДУ(без док.).

Если n решений y_1, y_2, …,y_n ЛОДУ у⁽ⁿ⁾ + P₁y^(n-1) +…+ P_n-1 y’ + P_n y = 0 линейно-независимы, на интервале (а,b) то определитель Вронского не может обращаться в ноль (0) ни в одной точке х ‌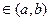| для любого Х из (а,b).

Следствие:

Определитель Вронского системы решений [y_1, y_2, …,y_n ] не равен 0 если система линейно независима, либо ‌ 0, если система линейно-зависима.

43. Теорема о структуре общего решения ЛОДУ (док). Понятие ФСР.

Опр: Система n линейно-независимого решения ЛОДУ n-го порядка называется ФСР

Теорема о структуре общего решения ЛОДУ

Если функции y₁(х)_, y₂(х)_, …,y_n(х) – образует ФСР ЛОДУ у⁽ⁿ⁾ + P₁y^(n-1) +…+ P_n-1 y’ + P_n y = 0, то y(х) = C₁y₁(x) + C₂y₂(x) + … + C_ny_n(x) = , есть общее решение этого уровня. (4).

Док-во:

Из теоремы о неравенстве нулю вронскиана линейно-независимых решений ЛОДУ:

Если n решений y_1, y_2, …,y_n ЛОДУ (2) и они линейно-независимы, на интервале (а,b) то определитель Вронского не может обращаться в ноль (0) ни в одной точке х ‌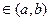| для любого Х из (а,b).

ð что (4) являются решением у⁽ⁿ⁾ + P₁y^(n-1) +…+ P_n-1 y’ + P_n y = 0

остается доказать, что можно подобрать const-ты то С₁, С₂, … С_n, таким образом что функция (4) удовлетворяет любой системе начальных условий [н.у.]

Задаем н.у., при x₀ 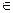(а,b) y(х₀) = y₀, y’(х₀) = y₀’, y^(n-1) (x₀) = y₀^(n-1) определяем C_1,C₂,…, C_n

Определение:

C₁y₁(x₀) + C₂y₂(x₀) + … + C_ny_n(x₀) = y₀

C₁y₁’(x₀) + C₂y₂’(x₀) + … + C_ny_n’(x₀) = y₀’, где y_1, y_2, y_n ФСР C₁ C₂ C_n const

………………………………………….. (5)

C₁y₁^(n-1)(x₀) + C₂y₂^(n-1)(x₀) + … + C_ny_n^(n-1) (x₀) = y₀^(n-1)

Определителем этой системы является определитель Вронского

W[y_1, y_2, …,y_n] 0, C_1,C₂,…, C_n - определяется един-м образом

Построим = C₁y₁(x) + C₂y₂(x) + … + C_ny_n(x),

согласно свойству (если y₁) α₁y₁ + α₂y₂ + …+ α_ny_n = 0 причем хотя бы одно h_i 0.

- является решением ДУ(2) = y(x), т.к. система (5) определена теми же н.у., что и y(x) ч.т.д.

Следствие:

1) максимальное число линейно-независимых решение ЛОДУ, коэффициенты непрерывны на (a,b) равно порядку этого уравнения.

2) независимо от н.у. все другие решения таких уравнений ЛОДУ является линейной комбинацией этих независимых решений (решений ФС)

3) Пространство решений ЛОДУ n-го порядка имеет базис из n-векторов, т.е. пространство n-мерное.

4) Для решения ЛОДУ n-го порядка необходимо найти ФСР. Общее решение получается как линейная комбинация решений ФС.

4 4. Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Вид частных решений, характеристическое уравнение (×)

ЛОДУ с постоянными коэффициентами

у⁽ⁿ⁾ + P₁y^(n-1) +…+ P_n-1 y’ + P_n y = 0, где все P_i (i= 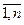)= const

будем искать частное решение y=e^kx, к – неизвестная постоянная

y’=ke^kx

y’’=k²e^kx

……

y⁽ⁿ⁾=k⁽ⁿ⁾ e^kx

 

k⁽ⁿ⁾ e^kx + P₁k^(n-1) e^kx + … + P_ne^kx = e^kx(k⁽ⁿ⁾ + P₁k^(n-1) + … + P_n) = 0

e^kx 0 => k⁽ⁿ⁾ + P₁k^(n-1) + … + P_n = 0, (1)

ð y=e^kx - решение ДУ

(1) – характеристическое уравнение для ЛОДу с постоянными коэффициентами, выражения слева характеристический многочлен.

Решением характеристич уравнения (1) дает систему частных решений ЛОДу, структура ФСР зависит от вида корней характер уравнения.

(1) – алгебраическое уравнение n-ой степени, может иметь не более, чем n корней, обознач-м эти корни характеристического уравнения через k₁,k₂ …k_n

Возможны случай

1)все корни хар-го уранения вещественны и различны

2)все корни различны, но среди них есть комплексные

3)среди действительных корней имеются кратные

4)среди комплексных корней есть кратные

Общий алгоритм решения ЛОДу с постоянным коэффициентом

1) составим характер уравнение: y=e^kx, k⁽ⁿ⁾ + P₁k^(n-1) + … + P_n = 0

2) найти корни характер уравнения k₁,k₂ …k_n

3) по характеру корней находим частное линейно-независимое решение по таблице 1

4) подставляем частное решение на основе Теоремы о структуре общего решения ЛОДУ и получаем общее решение y =

№	Вид корня	Соответственное решение
	Действ корень кратности 1	ekx
	Пара корней a bi;кратнос 1	eаxcosbx, eаxsinbx
	Действит корень кратност α	ekx, хekx, х2ekx, х3ekx,…, хα-1ekx
	Пара сопряж корней α a bi	eаxcosbx, eаxsinbx хeаxcosbx, хeаxsinbx х2eаxcosbx, х2eаxsinbx хα-1eаxcosbx, хα-1eаxsinbx

 

4 5. Линейные неоднородные дифференциальные уравнения n-го порядка. Теорема о структуре общего решения (док. для n=2). Теорема о суперпозиции решений (док. для n=2).

ЛНДУ

у⁽ⁿ⁾ + P₁y^(n-1) +…+ P_n-1 y’ + P_n y = f(x) (1) P_i – непрерывна на отрезке (a,b)

Теорема о структуре общего решения ЛНДУ

Общее решение ЛНДУ есть сумма частного решения и общего решения соответственного ему однородного уравнения

Док-во:

Для уравнения 2-го порядка (но теорема применима для уравнений любого порядка)

n=2

(1’) y” + P₁(x) y’ + P₂(x) y = f(x)

Обозначим у*(х) – частное решение ЛНДУ

(х) – общее решение ЛОДУ

Показать, что

(2) у= у*+ - общее решение ЛНДУ

Найдем:

Дважды дифференцируем функцию (2) и подставляем у, y’,y” в (1’)

у*”(x) + ”(x) + P₁(x)[ у*(x)+ ’(x)] + P₂(x)[ у*(x)+ (x)] =

= [у*”(x)+ P₁(x) у*’(x)+ P₂(x) у*(x)] + [ ”(x) + P₁(x) ’ (x)+ P₂(x) (x)] = f(x) + 0 = 0

= C₁y₁(x) + C₂y₂(x), y_1,y₂ – частное решение ЛОДУ y” + P₁y’ + P₂ = 0

C₁C₂ – подбираем так, чтобы они удовлетворяли начальным условиям

y(x₀)=y₀, y’(x₀)=y₀’, для любых х₀ 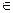(а,в), и любых y₀,y₀’

C₁y₁(x₀) + C₂y₂(x₀) + у*(x₀) = y₀

C₁y’₁(x₀) + C₂y’₂(x₀) + у*(x₀) = y₀’

Линейная неоднородная система, определитель этой системы, определитель Вронского

W[y_1, y₂]≠0 =>система имеет единственное решение при любых ₀ , ’₀ ,y*_0,y*’₀, это означает у= у*+ - общее решение ЛНДУ

Теорема2 принцип суперпозиции (принцип сложения решений)

Если функция y_i(x) является решением ЛНДУ

(3) y⁽ⁿ⁾ + P₁y^(n-1) + … + P_ny = f_i(x) то функция = α₁y₁ + α₂y₂ + … + α_ny_n, то это функция является решением y⁽ⁿ⁾ + P₁y^(n-1) + … + P_ny = α₁ f₁(x) + α₂ f₂(x) + … + α_n f_n(x) (4)

Док-во: для n=2

Подставим y, y’, y”, в (4), учитываем что y₁ y₂ решение соответственного уравнения (3)

α₁y₁” + α₂y₂” + P₁(x)[ α₁y₁+ α₂y₂] =

= [α₁y₁” + P₁(x)α₁y’₁ + P₂(x)α₁y₁] + [α₂y₂” + P₁(x)α₂y’₂ + P₂(x)α₂y₂] = α₁f₁(x) + α₂f₂(x)

46. Линейные неоднородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Метод неопределенных коэффициентов для уравнений со специальной правой частью. Метод вариации произвольных постоянных (вывод рабочей формулы).

Рассмотрим ЛНДУ с постоянными коэф-ми.

Ур-е у⁽ⁿ⁾ + P₁y^(n-1) +…+ P_n-1 y’ + P_n y = f(x): Pi=const

Метод неопр-х коэф-в можно применять если правое ур-е имеет следующий вид: f(x)= , , -многочлены степени g и r соотв-но a и b некоторые числа. В основе метода неопр-х коэф-в лежит знание формы частного решения, а именно частное решение стоит искать в аналогич-ой форме свободного члена.

№	Вид правой части (f(x))	Корни харак-го уравнения	Вид частного решения y*
	P

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: