 |
Знакопеременные ряды. Абсолютная и условная сходимость. Теорема об абсолютно сходящемся ряде(док).
|
|
|
|
Знакопеременные ряды - это ряды, которые содержат бесконечно много положительных и бесконечно много отрицательных членов. На ряду со знакопеременным рядом рассматривается ряд из абсолютных значений членов знакопеременного ряда.
 -знакопеременный ряд.(1)
-знакопеременный ряд.(1)
 -знакоположительный ряд.(2)
-знакоположительный ряд.(2)
Теорема (критерий сходимости знакопеременного ряда).
Если ряд (2) сходится, то и ряд (1)- сходится.
Доказательство:
 частичные суммы рядов (1) (2) соответственно.
частичные суммы рядов (1) (2) соответственно.
Обозначив через  - сумму положительных членов ряда (1),
- сумму положительных членов ряда (1),  - сумму отрицательных членов ряда(1).Тогда
- сумму отрицательных членов ряда(1).Тогда  =
=  -
-  ;
;  =
=  -
- 
Так как ряд (2) сходится, то существует конечный предел его частичных сумм  =
= 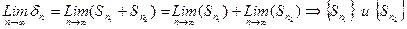 -ограничены.
-ограничены.
Так как ряд (2) знакоположительный, то  - будут возрастающие, следовательно по теореме Вейерштрасса существует конечный предел этих последовательностей (
- будут возрастающие, следовательно по теореме Вейерштрасса существует конечный предел этих последовательностей ( )
)
Рассмотрим  - число конечное, следовательно (1)- сходится. Ч.Т.Д.
- число конечное, следовательно (1)- сходится. Ч.Т.Д.
При исследовании знакопеременного ряда на сходимость нужно всегда рассматривать ряд из абсолютных величин членов этого ряда.
Определение:
Знакопеременный ряд  называется абсолютно сходящимся, если сходится знакоположительный ряд
называется абсолютно сходящимся, если сходится знакоположительный ряд  ,составленный из абсолютных значений его членов.
,составленный из абсолютных значений его членов.
Теорема (об абсолютно сходящемся ряде).
Если ряд  сходится, то знакопеременный ряд
сходится, то знакопеременный ряд  тоже сходится.
тоже сходится.
Доказательство:
 для ряда
для ряда  ;
;  для ряда состав.
для ряда состав.  из модулей.
из модулей.
 сходится по признаку сравнения.
сходится по признаку сравнения.
Признак этой теоремы является достаточным, но не является необходимым.
Ряд  -сходится; ряд
-сходится; ряд  - расходится.
- расходится.
Определение:
Знакопеременный ряд  называется условно сходящимся, если он сходится по признаку Лейбница, но ряд из абсолютных величин его членов расходится.
называется условно сходящимся, если он сходится по признаку Лейбница, но ряд из абсолютных величин его членов расходится.
55. Знакочередующиеся ряды. Теорема Лейбница (док.).
|
|
|
Знакочередующиеся ряды - это ряды, члены которых поочерёдно то положительны, то отрицательны.
Теорема Лейбница.
Если  =0 (1) и un
=0 (1) и un  un+1>0, n=1,2,…,(2) то знакочередующийся ряд
un+1>0, n=1,2,…,(2) то знакочередующийся ряд 
(3) сходится.
Доказательство:
Рассмотрим частичные суммы четного порядка ряда (3):
S2k=  . Их можно записать в виде S2k=(u1-u2)+(u3-u4)+…+(u2k-1-u2k), k=1,2,…
. Их можно записать в виде S2k=(u1-u2)+(u3-u4)+…+(u2k-1-u2k), k=1,2,…
В силу условия (2) выражения в круглых скобках неотрицательны и потому S2k  S2(k+1), т.е. последовательность частичных сумм четного порядка ряда (3) монотонно возрастает.
S2(k+1), т.е. последовательность частичных сумм четного порядка ряда (3) монотонно возрастает.
Замечая, что частичные суммы S2k можно записать также и в виде S2k=u1-(u2-u3)-…-(u2k-2-u2k-1)-u2k, k=1,2,…, и что выражения в круглых скобках в силу условия (2) неотрицательны, а u2k>0, получаем, что S2k<u1, т.е. последовательность {S2k} ограничена сверху.
Из монотонного возрастания и ограниченности сверху последовательности {S2k} следует, что она сходится.
Пусть  =S (4). Покажем, что и частичные суммы нечетного порядка ряда (3) стремятся к тому же пределу. Действительно, S2k+1=S2k+u2k+1, k=1,2…(5), и так как, согласно (1),
=S (4). Покажем, что и частичные суммы нечетного порядка ряда (3) стремятся к тому же пределу. Действительно, S2k+1=S2k+u2k+1, k=1,2…(5), и так как, согласно (1),  , то в силу (4) и (5) имеем
, то в силу (4) и (5) имеем  (6). Из (4) и (6) следует что
(6). Из (4) и (6) следует что  .
.
Теорема доказана.
56. Функциональные ряды. Основные понятия: область и точка сходимости, равномерная сходимость. Теорема Вейерштрасса (док.).
Функциональным называется ряд, члены которого есть непрерывные функции от x u1(x)+u2(x)+u3(x)+…+un(x)+…=  un (x).
un (x).
Совокупность значений аргумента, при которых функ-й ряд сходится, называется областью сходимости ряда.
Функциональный ряд  un(x) называется равномерно сходящимся в некоторой области x, если для каждого сколь угодно малого числа
un(x) называется равномерно сходящимся в некоторой области x, если для каждого сколь угодно малого числа  >0 найдётся такое целое положительное число N(
>0 найдётся такое целое положительное число N( ), что при n>N выполняется неравенство
), что при n>N выполняется неравенство 
 =
=  <
<  для всех x из области X.
для всех x из области X.
При этом сумма S(x) равномерно сходящегося функционального ряда есть непрерывная функция.
Достаточным признаком равномерности сходимости является
Признак Вейерштрасса.
Если члены функционального ряда U1(x)+U2(x)+…+Un(x)+… по абсолютной величине не превышают в некоторой области соответствующих членов сходящегося знакоположительного ряда a1+ a2+…+an+…, (an>0) т.е.
|
|
|
|U1(x)|  a1, |U2(x)|
a1, |U2(x)|  a2, |U3(x)|
a2, |U3(x)|  a3, … |Un(x)|
a3, … |Un(x)|  an, …
an, …
То функциональный ряд в области сходиться абсолютно и равномерно (правильно).
Знакоположительный числовой ряд  называется мажорирующим рядом или мажорантой для данного функционального ряда.
называется мажорирующим рядом или мажорантой для данного функционального ряда.
Т. Вейерштрасса. Если существует такая числовая последовательность {an}, что  =0, аn
=0, аn  (1),
(1), 
 (2) для всех n=1,2… и всех х
(2) для всех n=1,2… и всех х  , то последовательность {
, то последовательность {  } равномерно на E сходится к функции
} равномерно на E сходится к функции  .
.
Доказательство. В силу условия (1) для любого  существует такой номер
существует такой номер  , что an<
, что an<  для всех
для всех  . Но тогда в силу условия (2)
. Но тогда в силу условия (2) 
 для всех
для всех  и всех х
и всех х  , а это и означает равномерную сходимость последовательности {
, а это и означает равномерную сходимость последовательности {  } к функции
} к функции  на множестве Е.
на множестве Е.
5 7. Свойство равномерно сходящихся функциональных рядов (без док.)
1) Сумма правильно сходящегося ряда есть функция непрерывная в области сходимости.
Свойства почленного дифференцирования и интегрирования правильно сходящихся рядов.
2) Если ряд  сходится равномерно к некоторой непрерывной функции S(x), и ряд из производных
сходится равномерно к некоторой непрерывной функции S(x), и ряд из производных  так же равномерно сходится, то его сумма S*(x) равна производной от суммы исходного ряда S*(x) =
так же равномерно сходится, то его сумма S*(x) равна производной от суммы исходного ряда S*(x) =  =(
=( )'= S'(x)
)'= S'(x)
3) Если ряд  сходится равномерно к некоторой непрерывной функции S(x), то ряд полученый из данного путем почленного интерирования
сходится равномерно к некоторой непрерывной функции S(x), то ряд полученый из данного путем почленного интерирования  равномерно сходится и имеет сумму S**(x), равную интегралу от суммы исходного ряда
равномерно сходится и имеет сумму S**(x), равную интегралу от суммы исходного ряда
S**(x)=  =
=  =
= 
58. Степенные ряды. Теорема Абеля (док.) (×)
Функциональные ряды вида  называются степенным рядом по степеням(z-z0), где a1 a2... an
называются степенным рядом по степеням(z-z0), где a1 a2... an  R -коэффициенты степенного ряда, называются степенными рядами.
R -коэффициенты степенного ряда, называются степенными рядами.
При z0=0 получим  .Степенной ряд при z=0 всегда сходится, если x не равен 0 то ряд может как сходиться так и расходиться.
.Степенной ряд при z=0 всегда сходится, если x не равен 0 то ряд может как сходиться так и расходиться.
Поскольку замена (z-z0)=t может свести к виду  то мы будем рассматривать ряд такого вида.
то мы будем рассматривать ряд такого вида.
Т. Абеля. Если степенной ряд  (1) сходится в точке z1≠0, то он сходится и при том абсолютно в точке z, у которого
(1) сходится в точке z1≠0, то он сходится и при том абсолютно в точке z, у которого  , если степенной ряд расходится в т. z2≠0, то он расходится в т z,
, если степенной ряд расходится в т. z2≠0, то он расходится в т z,  .
.
Доказательство.
По условию  - то по необходимому признаку сходимости ряда
- то по необходимому признаку сходимости ряда  , т.к. сх-ся числ. послед. ограничена то существует M>0 |
, т.к. сх-ся числ. послед. ограничена то существует M>0 |  а n=0,1,2… Если
а n=0,1,2… Если  , то
, то  и следовательно
и следовательно  , являясь геометрической прогрессией со знаменателем
, являясь геометрической прогрессией со знаменателем  <1, сходится. Поэтому по признаку сравнения сходится и ряд
<1, сходится. Поэтому по признаку сравнения сходится и ряд  , а это означает абсолютную сходимость ряда (1) при
, а это означает абсолютную сходимость ряда (1) при  .
.
|
|
|
Пусть числовой ряд  расходится, =>
расходится, =>  для любого z |
для любого z |  . Предположим противное, те
. Предположим противное, те 
 сходится. По доказательству в 1 части теоремы из сходимости ч.р.
сходится. По доказательству в 1 части теоремы из сходимости ч.р.  => абсолютная сходимость
=> абсолютная сходимость  ,для любого
,для любого  , а значит этот ряд должен сходиться абсолютно, что противоречит условию => он расходится.
, а значит этот ряд должен сходиться абсолютно, что противоречит условию => он расходится.
59. Свойства степенных рядов(без док.). Ряды Тейлора и Маклорена (×)
Свойства степенных рядов:
1) Сумма степенного ряда является непрерывной функцией в интервале сходимости.
2)Степенные ряды  и
и  имеют один и тот же радиус сходимости.
имеют один и тот же радиус сходимости.
3)Степенные ряды можно почленно дифференцировать в интервале сходимости любое число раз и для S(x).

4)Степенной ряд можно почленно интегрировать по любому промежутку, принадлежащему интервалу сходимости.
Понятие о ряде Тейлора:
Всякая функция при соблюдении определённых условий в интервале, содержащем точку  ,может быть представлена в нём в виде степенного ряда, и этот ряд будет её рядом Тейлора.
,может быть представлена в нём в виде степенного ряда, и этот ряд будет её рядом Тейлора.
Опр-е: Рядом Тейлора функции f(x) называется степенной ряд вида:

Рядом Маклорена функции f(x) называется ряд:

Ряды Тейлора и Маклорена есть разложение функции в ряд по степеням ( ) и
) и  соответственно,или представление функции в окрестности точек
соответственно,или представление функции в окрестности точек  или
или  степенным рядом.
степенным рядом.
Коэффициенты рядов Тейлора и Маклорена вычисляются через значения производных функции всех порядков в точках  =
=  и
и  = 0 соответственно.Но существование производных любого порядка не является достаточным условием разложимости функции в ряд Тейлора.
= 0 соответственно.Но существование производных любого порядка не является достаточным условием разложимости функции в ряд Тейлора.
Достаточное условие разложения функции в ряд Тейлора:
Всякая функция 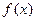 ,бесконечно дифференцируемая в интервале
,бесконечно дифференцируемая в интервале 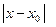 < r,может быть разложена в этом интервале в сходящийся к ней степенной ряд, называемый рядом Тейлора,если в этом интервале остаток ряда
< r,может быть разложена в этом интервале в сходящийся к ней степенной ряд, называемый рядом Тейлора,если в этом интервале остаток ряда 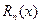 стремится к нулю
стремится к нулю 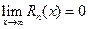 .
.
Остаток ряда Тейлора можно записать в форме Лагранжа 
где С некоторая произвольная точка рассматриваемого интервала.
Условие 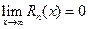 выполняется,если производные всех порядков функции ограничены некоторым числом
выполняется,если производные всех порядков функции ограничены некоторым числом 
|
|
|
Если записать ряд Тейлора вместе с остаточным членом,то получим формулу Тейлора:

6 0. Признак сходимости ряда Тейлора к порождающей его функции (док).
Теорема: Если степенной ряд по степеням  сходящийся к функции
сходящийся к функции 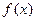 в окружности т.
в окружности т.  , то он является рядом Тейлора функции
, то он является рядом Тейлора функции 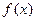 в окружности т.
в окружности т.  .
.
Док-во: Пусть в окружности т.  степенной ряд по степеням
степенной ряд по степеням  сходящийся к ∞-ой дифференцируемой функции
сходящийся к ∞-ой дифференцируемой функции 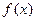 т.е
т.е 

продифференцируем степенной ряд:

при 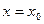 получаем:
получаем:
 Ч.т.д.
Ч.т.д.
|
|
|


