Математико-статистические методы обработки экспертных оценок

Математико-статистические методы обработки экспертных оценок — методы, предназначенные для повышения достоверности результатов оценки качества товаров экспертами.

Подразделяются на четыре подгруппы методов: ранжирования, непосредственной оценки, последовательных предпочтений и парных сравнений.

Ранжирование — метод, основанный на расположении объектов экспертизы в возрастающем или убывающем порядке.

Предназначен для решения многих практических задач, когда объ­екты, определяющие конечные результаты, не поддаются непосредст­венному измерению. Кроме того, отдельные объекты, характеризую­щиеся различной природой, оказываются несоизмеримыми, поскольку у них нет общей меры сравнения. Основанием для применения ранжи­рования служит необходимость упорядочения какого-либо объекта во времени и пространстве, а также в соответствии с измеряемым качест­вом без проведения точных измерений. И наконец, в ситуации, когда измеряемое качество в принципе не может быть измерено по причинам практического и теоретического характера.

Процедура ранжирования состоит в расположении экспертом объек­тов в наиболее рациональном порядке и присвоении им определенного ранга в виде чисел натурального ряда. При этом ранг 1 получает наибо­лее предпочтительный объект, а ранг п — наименее предпочтительный. В результате получается шкала порядка, в которой число рангов равно числу объектов. Если два объекта имеют одинаковые ранги, им припи­сывают так называемые стандартизированные ранги, которые рассчиты­ваются как среднее суммы мест объектов с одинаковыми рангами.

Например, шести объектам присвоены следующие ранги:

1 2 3 4 5 6 1 2 3 3 2 3

Объекты 2 и 5 поделили 2-е и 3-е места. Их стандартизированный ранг будет равен

(2 + 3)/2 = 2,5.

Объекты 3, 4 и 6 поделили 4-е, 5-е и 6-е места, а их стандартизи­рованный ранг равен 5:

(4 + 5 + 6)/3 = 5.

Глава 4. Методы товарной экспертизы

§ 5. Экспертные методы

 

В результате получается следующая ранжировка:

12 3 4 5 6

1 2,5 5 5 2,5 5"

Таким образом, сумма рангов S_n, полученная в результате ранжи­рования п объектов, будет равна сумме чисел натурального ряда:

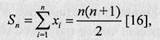
где X,- — ранг /-го объекта.

Метод ранжирования редко применяется в чистом виде. Чаще все­го он сочетается с методом непосредственной оценки или его моди­фикациями (ранжированием по сумме оценок, комбинированным способом и др.).

Метод непосредственной оценки состоит в том, что диапазон изме­нения какой-либо количественной переменной разбивается на несколько интервалов, каждому из которых присваивается определенная оценка в баллах, например от 0 до 10. Эксперт должен включить каждый объект в определенный интервал в зависимости от его значимости.

В некоторых случаях для выбора наиболее предпочтительного фактора оказывается удобнее сначала провести оценку, а затем — ранжирование.

Метод последовательных предпочтений — метод, основанный на сравнении отдельного объекта с суммой последующих объектов для установления его важности.

Данный метод разработан У. Черчменом и Р. Акофом и предна­значен для проведения сравнений с учетом определенных допусков. Основные из этих допусков заключаются в следующем:

• каждому результату оценки объекта соответствует действитель­
ное неотрицательное число V_t, рассматриваемое как оценка ис­
тинной значимости Q_t;

• если результат Q_t более важен, чем Q_k, то FJ > V_k, и если Q_t равно­
значен Qh то Vi = V_k;

• если оценки V_t и V_k соответствуют результатам Q_{ и Q_k, то оценка
Vi + V_k соответствует общему результату Q_t и Q_k\

• если результат Q_t предпочтительнее Q_k или Q_k предпочтительнее Qi, то совместный результат Q_t и Q_k предпочтительнее Q}. Порядок представления результатов или их группировка не влия­ют на предпочтения.

Если значимость объекта ниже, чем сумма всех остальных, то он корректирует оценки:

Процедура последовательных сравнений состоит в следующем. Эксперту представляется ряд объектов (показателей, факторов, резуль­татов), которые необходимо оценить по их относительной важности (значимости), и он производит ранжирование. Наиболее важному объ­екту присваивается оценка, равная 1, а остальным объектам — оценки ниже 1 до 0 в порядке их относительной важности. Затем эксперт уста­навливает, является ли объект с оценкой 1 более важным, чем сумма остальных факторов. Если важность объекта велика, то он увеличивает оценку Vi, чтобы она была больше, чем сумма всех остальных:

Далее аналогичной процедуре подвергаются все остальные объек­ты, значимость которых проверяется в сравнении с суммой всех ос­тавшихся.

Таким образом, используемая процедура состоит в систематиче­ской проверке оценок путем их последовательного сравнения.

Метод последовательных предпочтений целесообразно приме­нять, если число сравниваемых объектов не превышает 7. При боль­шем количестве объектов их необходимо разбивать на подмножества, включающие 6 объектов. В тех случаях, когда это невозможно, следу­ет использовать метод парных сравнений.

Метод парных сравнений — метод, основанный на сравнении объектов экспертизы попарно для установления наиболее важного в каждой паре.

Глава 4. Методы товарной экспертизы

§ 5. Экспертные методы

 

Для облегчения процедуры составляют матрицы парных сравне­ний, в которых все объекты (факторы) записывают в одном и том же порядке дважды: в верхней строке и крайнем левом столбце. Каждый эксперт должен проставить на пересечении строки и столбца оценку для двух сравниваемых факторов. В зависимости от того, какой фак­тор является наиболее предпочтительным, эта оценка будет равна со­ответственно 1 или 0. В главной диагонали такой матрицы простав­ляются прочерки или нули (табл. 6).

Каждая пара факторов может сравниваться единожды или дважды.

Существуют различные варианты частичного парного сравнения:

• выбор предпочтительного объекта из заранее сгруппированных
пар;

• частичное парное сопоставление одной группы объектов со всеми
другими, тогда как остальные факторы сопоставляются с некото­
рыми другими;

• установление суммарных рангов факторов.

Таблица 6

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: