С учетом априорной информации

Для повышения достоверности оценок показателей надежно­сти высоконадежных и малосерийных ЭА можно использовать ме­тоды учета априорной информации. Принято всю информацию о надежности ЭА подразделять на текущую и априорную. Первую получают в результате наблюдений при эксплуатации ЭА; под вто­рой обычно понимается информация о надежности, существующая независимо от текущей, ее получают в результате расчетов и моде­лирования надежности, различного рода испытаний на надежность, эксплуатации ЭА, конструктивно близких к исследуемому.

С точки зрения системного подхода любое исследование надеж­ности ЭА должно планироваться и проводиться именно с учетом результатов предыдущих исследований, т. е. с учетом априорной информации.

Наиболее разработанными методами использования априорной информации при анализе надежности можно считать [11]:

■ метод линейного объединения априорной и текущей информа­ции;

■ метод, использующий рандомизацию искомого показателя и теорему Байеса;

■ метод, использующий частичную априорную информацию;

■ метод объединения неоднородной априорной информации;

■ метод коррелированных процессов.

Рассмотрим наиболее распространенные.

Метод линейного объединения априорной и текущей информа­ции. Предположим, что проведено п серий испытаний однотипных ЭА на надежность, по результатам которых получено п значений оценок интенсивностей отказов 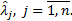Считаем, что оценки несмещенные с известными дисперсиями . Требуется найти функцию интенсивности отказов , учитывающую каждую из оценок λ_j. Наиболее простым методом решения этой задачи явля­ется метод линейного объединения

(11.21)

где d — весовая функция.

Если опустить промежуточные выкладки, то в окончательном виде выражение для объединения оценок имеет вид

(11.22)

с дисперсией

Если — оценки, полученные на этапе эксплуатации, а —оценки по данным априорных исследований надежно­сти, то

(11.23)

Выигрыш в точности полученных оценок за счет использова­ния априорной информации:

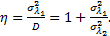(11.24)

Объединение оценок с использованием выражений (11.23) и (11.24)возможно только в случае известных дисперсий . Пре­имуществом метода линейного объединения оценок характеристик надежности является необязательное знание законов распределе­ния исследуемых случайных величин.

Метод, использующий рандомизацию искомого показателя и теорему Байеса. Теорема Байеса широко применяется для учета априорной информации в задачах оценивания показателей надеж­ности. Формула Байеса для дискретных случайных величин имеет вид

(11.25)

где А и B — зависимые случайные события; P(A_j)— вероятность события A_j из группы несовместных событий А_j,P (B/A_j) — веро­ятность события В при условии свершения события А_j.

В случае непрерывных случайных величин формула Байеса такова:

(11.26)

где h (θ)— априорная плотность распределения параметра θ ∊ 𝚯; f (θ, t)— плотность распределения параметра θ; h(θ/Т = t) — апо­стериорная плотность распределения параметра θ при условии, что в результате наблюдений реализована статистика Т.

Пусть в результате текущих исследований группы однотипных ЭА была получена статистика об отказах — наработка до отказа i -го ЭА с функцией распределения F(θ, t) и плотностью f (θ, t).

В общем случае 𝚯 — вектор параметров закона распределения, θ ∊ 𝚯. Предположим, что существует априорная информация о на­дежности исследуемых ЭА: — априорная статистика наработок до отказа. Будем считать, что случайные величины T_i и T_j имеют одну и ту же теоретическую функцию распределения, т. е. априорная и текущая информация однородны. Требуется оценить параметр θ по результатам текущей и априорной информации.

Согласно теореме Байеса апостериорная плотность распреде­ления параметра θ:

(11.27)

где h (θ) — априорная плотность параметра θ, определенная по ста­тистике { T_j }:

Следует пояснить, что если в качестве оценки параметра при­нять условное математическое ожидание значения θ, предположив, что произведены наблюдения текущих то оценка

обеспечивает минимум средней квадратической ошибки. При этом, чем точнее рассчитано апостериорное распределение , тем выше точность . Таким образом, даже при относительно малом объеме статистики об отказах использование априорной информации позволяет существенно повысить точность оценки характеристик надежности ЭА.

Известно также, что если первоначально принимаемое распре­деление оцениваемого параметра носит в значительной мере слу­чайный характер, то этого нельзя сказать об апостериорном рас­пределении. Согласно теореме Бернштейна — фон Мизеса, если априорная плотность распределения параметра θ непрерывна, то по мере возрастания числа наблюдений апостериорное распреде­ление стремится к пределу, не зависящему от априорного распре­деления.

В качестве примера в табл. 11.4 приведены выражения для оценивания параметров различных законов распределения, рас­пространенных в теории надежности.

 

 

11.4.

СИСТЕМЫ СБОРА ИНФОРМАЦИИ

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: